自然数|这可能是世上最美丽的函数( 五 ) 定义|函数|方式|答案|对数|利昂

文章图片

黎曼Zeta方程
它对数论非常重要，原因之一就是它与黎曼Zeta方程有特殊的关系。我们再来看一下定义，但这一次围绕着一个替换展开。令n为自然数，然后作替换t=nx ，我们得到：

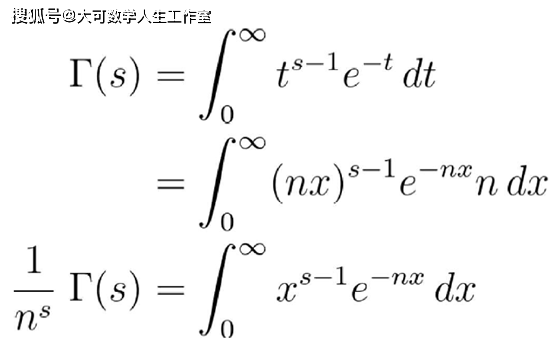
文章图片

由于这一结果对任何自然数n成立，我们可以对两边取和，得到

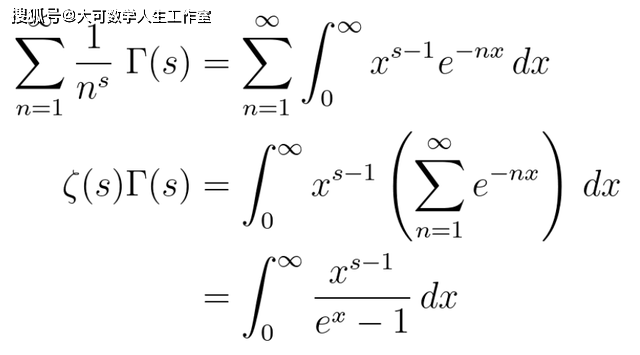
文章图片

于是我们得到了关于Zeta函数和Gamma函数的美丽关系：

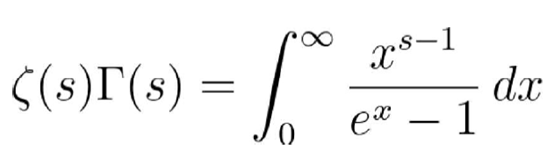
文章图片

然而，这只对Re(s)>1成立。
这是两个函数具有紧密关系的第一个提示。一个更深层次且更有趣的结果，也是我认为世界上最为美丽的函数方程，就是下面这个(这里我们不证明，直接给出)：

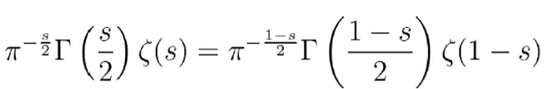
文章图片

伯恩哈德·黎曼(Bernhard Riemann)在1859年发现了它，它通过Gamma方程给出了Zeta方程的很多信息。
例如，在负偶数整数处可以清楚地看到ζ的平凡零点。这是因为，通过解析地将Γ(s)延续到整个复平面，我们看到它在非正整数处有极点。因为左边的Gamma因子在负偶数整数处发生blow up ，而右边是有限的，所以在这些点上ζ(s)必须为零。
在理论物理学中， Euler发现的Beta函数，在1968年被意大利理论物理学家加布里埃尔·维尼齐亚诺(Gabriele Veneziano)用来描述强相互作用的介子。欧拉Beta函数可以定义为 B(x,y)=Γ(x)Γ(y)/Γ(x+y) 。这是因为它描述了弦论中第一个已知的散射振幅，在某种意义上是解决这个问题的唯一方法。这也与Γ的负整数的极点有关。
另一个非常漂亮的结果是Gamma函数的增长。这就是所谓的斯特林公式：

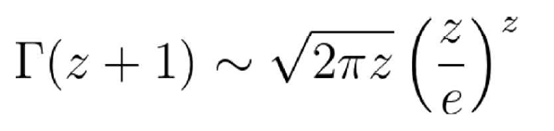
文章图片

这意味着上面两个边的增长的量级是相同的，即当z趋于无穷大时，它们的比值的极限趋于1 。
欧拉令人惊奇的积分公式
在推导Γ(s)ζ(s)的积分公式时，我们对两边求和，并构建一些级数。欧拉没有这样做，他做了一些辉煌的事情。他做了一个更一般的替换，然后他的头脑爆发出创造力，最终提出了一个包含各种有趣的东西的惊人的公式。让我们看看他是怎么做到的，以及这些公式是什么。

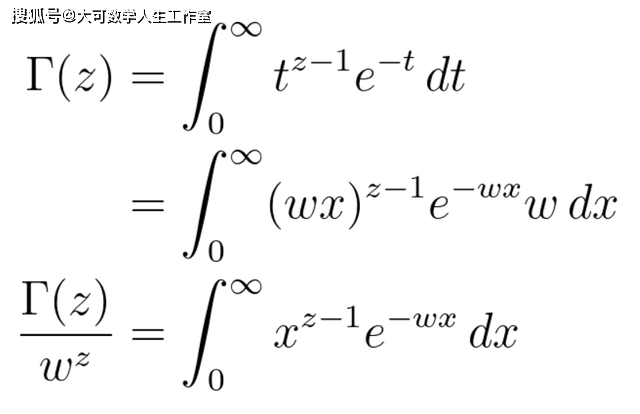
文章图片

在欧拉的时代，人们对复数分析了解并不多，但欧拉具有一个奇妙的直觉，因为他知道当w是一个正实数时，这个关系是成立的。他还考虑了当w是复数，且w的实部大于0的情况，假设w属于复数且w实部大于0 ，通过对上面方程的两边求共轭，可以得到：

自然数|这可能是世上最美丽的函数( 五 )

推荐阅读

彻切伤口化脓该怎么办？

人生哲理的文字控说说;真正成熟的人，崩溃都是没有声音的

怒江车辆报废办理地址大全怒江车辆报废办理地址大全电话

宝宝三个月吃手如何解决

hik作为网名是什么意思

近视4点8是多少度

腌生蚝怎样做腌生蚝的做法

中国哪里产大量的蓝莓

如何设置手机微信的文章阅读功能

什么是非连续性文本

什么能使卤肉增香

油炸薯条的危害是什么

元宵节活动邀请函内容

身体这处上翘婚姻竟不能长久

老年人预防骨质疏松吃什么？老年人怎样预防骨质疏松？

装修除了北欧风还有什么风你还知道哪些好看的装修

抑郁症一定要坚持吃药吗

鲈鱼养殖怎么样

洛神草莓果酱的做法（其它国家）

中国以及国人在历史与未来中该怎样在国际舞台上自处