自然数|这可能是世上最美丽的函数( 二 ) 定义|函数|方式|答案|对数|利昂

如你所见，阶乘函数增速惊人。它是超指数的(super-exponential)：它比指数增长得还快。
Gamma 函数
凡是欧拉思考的问题，最终一般都能解决。但是，真正的伟大之处在于他解决问题的方式。接下来你会发现，他那富有创意的思路和天外来客般的想法是如此智慧。
1738年，欧拉用一种积分形式推广了阶乘的定义：

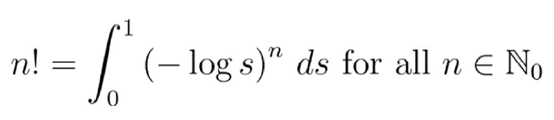
文章图片

这里的log是自然对数(有时写作ln) 。我们做一个替换：s=exp(-t) ，这里的exp是以e(这个数字也是欧拉发现的)为底的对数，我们得到：

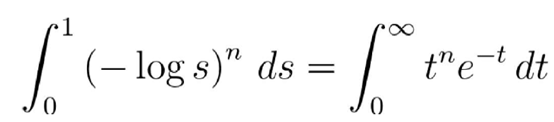
文章图片

于是我们就得到了这个漂亮的结果：

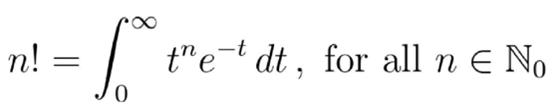
文章图片

这就是欧拉的定义。要证明这个积分等于阶乘，我们把右侧的积分叫做Π(n) ，然后分部积分：

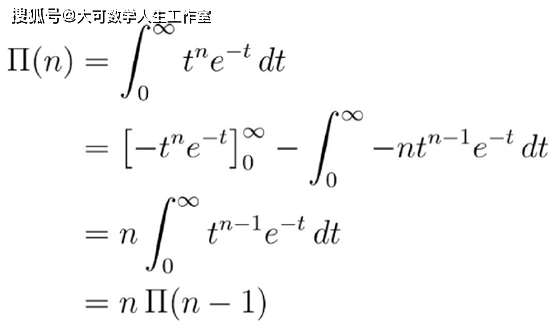
文章图片

利用这个函数方程，我们就可以用归纳法来证明上面的公式。我们想要证明Π(n)=n！对任何自然数n成立。首先，注意：

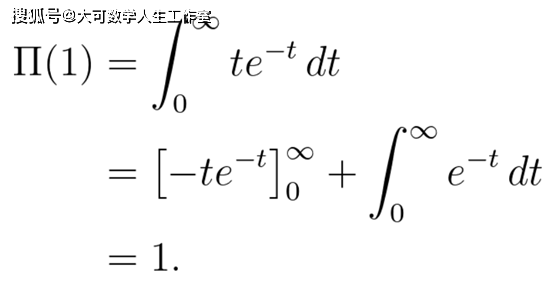
文章图片

即， Π(1)=1!
然后，假设Π(n-1)=(n-1)! ，那么我们有 Π(n)=nΠ(n-1) =n(n-1)!=n!
这里用到了上面的函数方程。根据归纳法，命题得证。注意，上面关于Π(n)的定义， n并不一定是自然数。这个表达式对所有实部为正的复数都是讲得通的。
处理广义阶乘的现代方法就是Gamma函数。 Gamma函数与刚刚的Π函数十分相似，定义如下：

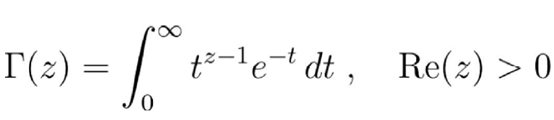
文章图片

注意：对任何自然数n ，有Γ(n)=Π(n-1)=(n-1)! 。因此， Gamma函数也满足一个相似的函数方程：Γ(z+1)= zΓ(z) 。
所以Gamma函数是广义的阶乘函数，因为对所有的非负整数n ，有Γ(n+1)= n! 。
但这是推广Gamma函数的唯一方式吗？
不幸的是，答案是否定的。然而，如果我们添加某种约束的话，它就是唯一的了。这个约束与对数凸性(logarithmic convexity)这个概念有关，因为稍微有点偏题，在这里就不详细讲了。具体的要求是函数logΓ是凸的。
★
TIP
★
一个二次可微的函数f是对数凸的，当且仅当

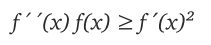
文章图片

自然数|这可能是世上最美丽的函数( 二 )

推荐阅读

玻璃门开不了怎么办，怎么样调整铝合金玻璃门不正的情况

吃苹果时太酸了有什么办法解决吗为什么煮了苹果之后会变酸

农村俗语“宁丢家财万贯，不舍房屋面南”是何道理？

《伊索寓言》的主要特点是什么

为什么男的肚子容易胖发胖的信号有哪些

葱烧小芋头的做法（素食菜谱）

豆角不熟会中毒吗

怎么改掉口吃结巴

要高考了不想学习怎么办？要高考了很烦怎么办？

安卓手机软件怎么升级

胸中缝的训练方法有什么方法呢？

平行四边形的面积公式是如何推导出来的你知道吗

经期可以喝的茶有哪些

啤酒销售技巧和话术

美宝莲双头眉笔好用吗？美宝莲双头眉笔怎么样？

卖对虾怎么养不死养虾小妙招

开网店推广费高吗

这段话你咋理解

百度网盘怎么分享链接

拌饭酱汁怎么调制一招搞定