
本文图片
图4:这些是产生空间填充曲线的前五个步骤 。 在每一步 , 曲线的面积为零 , 但在极限情况下 , 它填充了正方形 。 这条特殊的曲线是由大卫·希尔伯特(David Hilbert)引入的 。
这些和其他令人惊讶的例子清楚地表明 , 数学家需要证明维度是一个真实的概念 。 例如 , 当n≠ m时 , n维和m维欧几里得空间的某些基本性质是不同的 。 这个目标被称为“维度不变性”(invariance of dimension)问题 。
终于 , 在1912年 , 在康托尔的发现之后将近半个世纪 , 在人们多次证明维数不变性的尝试失败之后 , 布劳威尔(L.E.J. Brouwer)使用自己创造的一些方法并取得了成功 。 从本质上讲 , 他证明了不可能将一个更高维的物体放入较低维度的空间中 , 以及在不将物体分成许多部分(如康托尔所做的那样)、不允许物体与自身相交(如皮亚诺所做的那样)的情况下 , 使用较低维度的物体填满较高维度的空间 。 此外 , 大约在这个时候 , 布劳威尔等人给出了各种严格的定义 , 例如 , 可以根据球在n维空间中的边界是n-1维这一事实 , 帮助归纳地确定维数 。
尽管布劳威尔的工作将维度概念置于强大的数学基础上 , 但它无助于增强我们对高维空间的直觉:对3维空间的熟悉太容易使我们误入歧途 。 正如托马斯·班乔夫 (Thomas Banchoff) 所写 , “我们所有人都是对自己所在维度存有偏爱的奴隶 。 ”
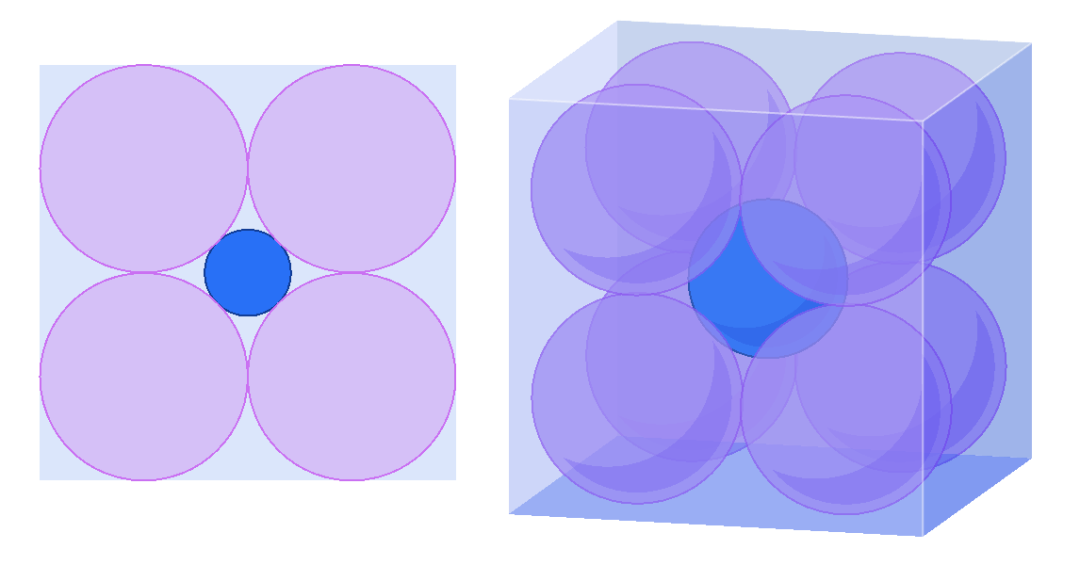
例如 , 假设我们将2n个半径为1的球体放置在边长为4的n维立方体中 , 然后将另一个球体放置在与它们中心相切的位置 。 随着n增加 , 中心球体的大小随之增加——它的半径为√n -1 。 但是 , 令人震惊的是 , 当n≥10时 , 这个球体会伸出立方体的边 。
本文图片
图5:中心球体随着维度的增加而变大 , 最终会突出到立方体外面 。
【立方体|几何、分形与时空:跨越百年的维度定义之旅】
高维空间中令人惊讶的现实导致统计和数据分析出现问题 , 统称为“维数灾难”(curse of dimensionality) 。 许多统计方法所需的样本点数量随维度增加呈指数增长 。 此外 , 随着维度增加 , 点形成聚类的概率会降低 。 因此 , 找到为高维数据降维的方法十分重要 。
3. 分形和非整数维度
维度的故事并没有因为布劳威尔而终结 。 仅仅几年之后 , 费利克斯·豪斯多夫(Felix Hausdorff)提出了一个新的维度定义 , 之后的数学发展证明该定义对现代数学至关重要 。
推荐阅读
- 技术|“2”类医械有重大进展:神经介入产品井喷、基因测序弯道超车
- 重大进展|“2”类医械有重大进展:神经介入产品井喷、基因测序弯道超车
- Tencent|原生版微信上架统信UOS应用商店:适配X86、ARM、LoongArch架构
- 国家|2022上海国际热处理、工业炉展览会
- IT|8号线、14号线将全线贯通 北京地铁?今年开通线路段创纪录
- 软件和应用|iOS/iPadOS端Telegram更新:引入隐藏文本、翻译等新功能
- Intel|Intel谈DDR5内存价格贵、缺货问题:新技术升级在所难免
- IT|宝马电动转型成果初显:i4、iX供不应求 新能源车销量已破百万
- 银行|银行卡、社保卡可直接刷卡坐公交 上海公交开始试点
- 概念股|孙佳山、张泰旗:警惕元宇宙可能带来的金融泡沫







