维度的概念乍一看似乎很直观 。 瞥一眼窗外 , 我们可能会看到落在纤细的旗杆上体验零维空间的乌鸦 , 被限制在一维电话线上的知更鸟 , 在二维地面上自由移动的鸽子 , 还有翱翔在三维空间的老鹰 。
但是对于数学家来说 , 为维度的概念找到一个明确定义实则异常困难 。 我们经过数百年的思想实验和富有想象力的比较 , 才得出目前对维度概念的严格理解 。
1. 超越三维
古人知道我们生活在三个维度中 。 亚里士多德[1]写道:“向一个方向延伸的是直线 , 两个方向延伸的是平面 , 三个方向延伸的是物体 。 除此之外就没有其他了 , 这些就是所有的维度 。 ”
然而相比于其他人 , 数学家更热衷于想象更多维度的思维训练:垂直于已知的三个维度的第四维度会是什么样子?
一种流行的方法:假设我们的可知宇宙是三维空间中的二维平面 。 一个在平面上方的实心球对我们来说是看不见的 。 但是如果它坠落并接触到平面 , 就会出现一个点 。 当它继续穿过平面时 , 圆盘会不断变大 , 直到达到其最大尺寸 , 然后缩小并消失 。 正是通过这些横截面 , 我们才能看到三维物体的形状 。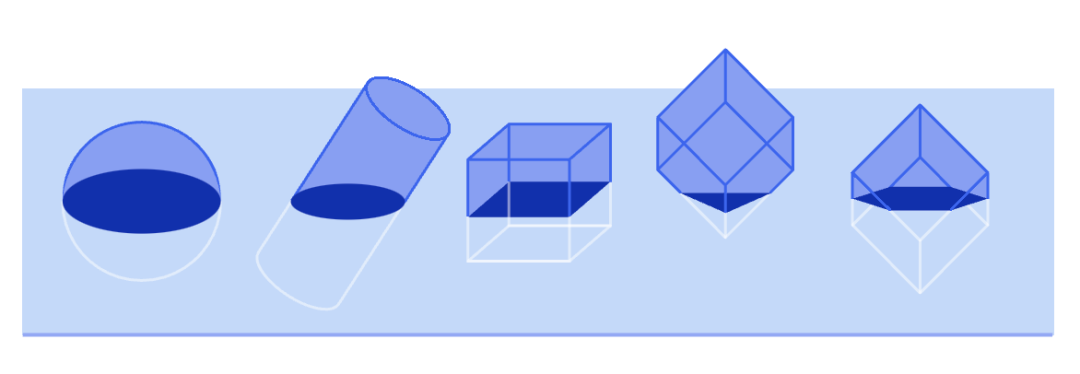
本文图片
图1:在平面上只能看到三维物体的横截面 。 | 来源:Samuel Velasco/Quanta Magazine
类似地 , 在我们熟悉的三维宇宙中 , 如果一个四维球穿过它 , 这个四维球会以一个点的形式出现 , 之后成为一个实心球 , 最终达到完整半径的球 , 然后半径减小并消失 。 这给了我们关于四维形状的感知 , 但是对于这样的物体 , 还有其他思考方式 。
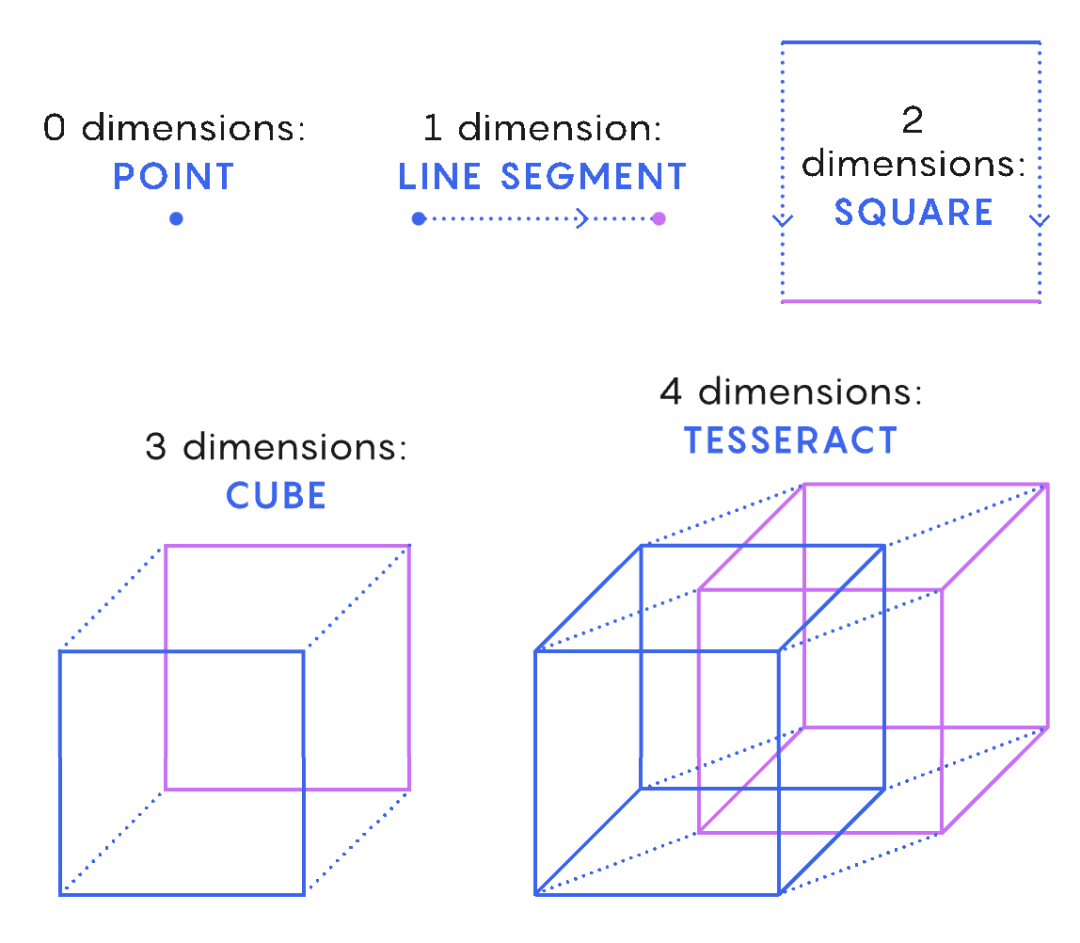
例如 , 让我们尝试通过构建超立方体来可视化立方体的四维等价物 。 如果我们从一个点开始 , 可以在一个方向上拖动它以获得一条线段 。 之后 , 当我们垂直于拖动方向移动线段时 , 得到一个正方形 。 在第三个垂直方向拖动这个正方形会产生一个立方体 。 同样 , 我们通过在第四个方向上拖动立方体来获得超立方体 。
本文图片
图2:通过将蓝色位置的图形拖动到紫色位置 , 我们可以可视化各种维度的图形 , 包括超立方体 。
或者 , 就像我们可以将立方体的面展开为六个正方形一样 , 我们可以展开超立方体的三维边界以获得八个立方体 , 正如萨尔瓦多·达利 (Salvador Dalí) 在 1954 年的画作《受难》(Crucifixion , Corpus Hypercubus) 中所展示的那样 。
推荐阅读
- 技术|“2”类医械有重大进展:神经介入产品井喷、基因测序弯道超车
- 重大进展|“2”类医械有重大进展:神经介入产品井喷、基因测序弯道超车
- Tencent|原生版微信上架统信UOS应用商店:适配X86、ARM、LoongArch架构
- 国家|2022上海国际热处理、工业炉展览会
- IT|8号线、14号线将全线贯通 北京地铁?今年开通线路段创纪录
- 软件和应用|iOS/iPadOS端Telegram更新:引入隐藏文本、翻译等新功能
- Intel|Intel谈DDR5内存价格贵、缺货问题:新技术升级在所难免
- IT|宝马电动转型成果初显:i4、iX供不应求 新能源车销量已破百万
- 银行|银行卡、社保卡可直接刷卡坐公交 上海公交开始试点
- 概念股|孙佳山、张泰旗:警惕元宇宙可能带来的金融泡沫







