考研数学咋开始复习( 七 )
在
处连续,则存在
时,使得
在
时连续.B.若
在
处可导,则存在
时,使得
在
时可导.C.若
在
的去心邻域内可导,在
处连续且
存在,则
在
处可导,且
.D.若
在
的去心邻域内可导,在
处连续且
不存在,则
在
处不可导.对于数学基础比较好的,很容易看懂选项,但是为了解释方便,我们解释几个概念!一点、去心邻域和包心邻域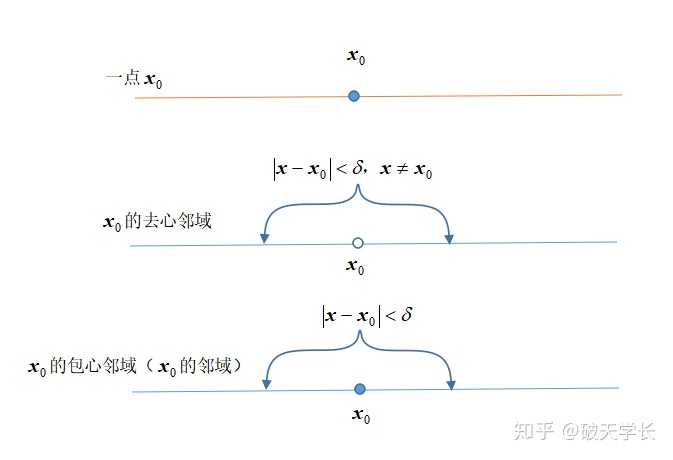
图中,
可理解为给定任意小的一个数。那么,将选项翻译成“人话”,即
A.一点连续
邻域连续B.一点可导
邻域可导C.去心邻域导数连续,包心邻域函数连续
一点可导且连续D.去心邻域导数不连续,包心邻域函数连续
一点不可导在分析这四句话之前,我们来探究一下“可导必连续”,这句话反过来说就是“不连续必然不可导”!!!这句话包括四个名词,即可导、连续、一点和邻域(去心和包心),排列组合包括一点连续、一点可导、邻域连续、邻域可导、一点导数连续等等情况,这五种情况又可以组合成如下图所示的10种情况,实际上再细分的话,情况更多!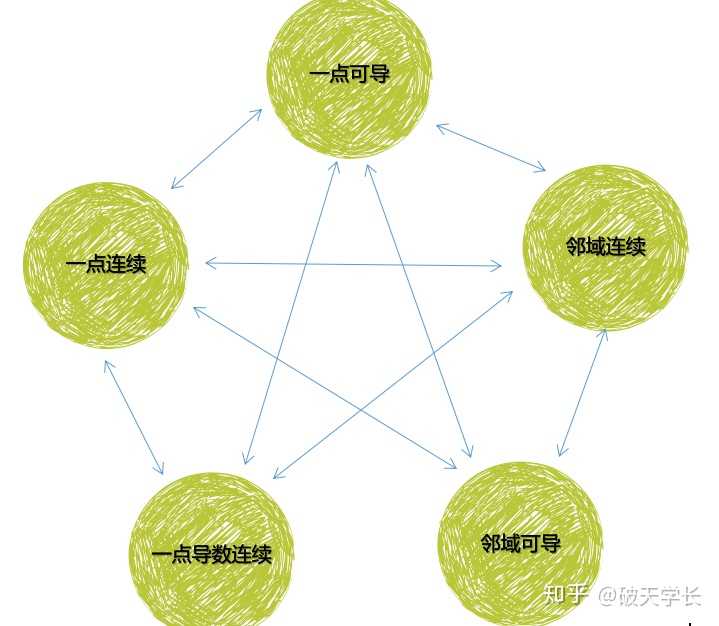
这么多种情况我们怎么解决?(请自己思考,本文将只分析例题涉及到的命题。)笔者总结概念定义这方面命题的证明,发现证真和证伪一般来说是要采取不同的手段的!证真:使用定义表达式!证伪:使用反例法!
证真时的定义表达式如何使用?举例说明,例如2020考研数学一的真题第2题
2.设函数
在区间(-1,1)内有定义,且
,则()A.当
,
在
处可导B.当
,
在
处可导C.当
在
处可导时,
D.当
在
处可导时,
推荐阅读
- 鱼泡咋烧好吃
- 学院风的女生又矮又胖要咋穿鞋?
- 咋样变得像立党一样优秀
- 大一小白女生咋一步一步变得时尚
- 鱼肚子里的一层黑膜是啥咋形成的能吃吗
- 咋判断摄影机的成像质量呢从哪些方面可以判断
- 男方是深圳户口,女方非深户,咋办理准生证将来宝宝咋办理深圳户口
- 沙漠 美卫星路过中国上空拍下惊人一幕,西方坐不住了到底咋做到的
- 胖mm咋穿裙子?
- 头大的窄肩瘦小矮妹子该咋搭配









