拓扑学提供了形状和连接性质的数学语言 , 它还可以用局部约束来描述整体结构 。 “拓扑学是绝妙的数学过滤器 , ”Hess讲解道 , 拓扑可以用来检测重建电路的结构以及连接性质 , 帮助人们理清各部分在大脑功能中扮演的角色 。
对于如何将拓扑这个过滤器应用于重建的微型电路及其31000个节点 , 800万个连接上 , Hess介绍了多种方法 。 她与同事所采用的方法是考虑能反映原网络显著特征的子网络 。 信息的流向在神经回路中至关重要 , 所以他们着重研究前馈子网络 , 这是指网络中的信息只沿一条路径传递 。
从拓扑的角度来说 , 这种结构可以用有向单纯形(Directed simplex)来表示 。 单纯形是三角形在任意维度下的推广:0-单纯形是一个点(节点);1-单纯形是一条线(节点之间的边);2-单纯形是我们熟悉的三角形(三个节点和三条边);4-单纯形是四面体(四个节点和六条边) , 等等 。 如果只考虑边有向的单纯形 , 那么一个前馈网络就可以由一个单纯形表示 , 而且这个单纯形中 , 方向指向完全向外的节点(网络的输入端) , 以及指向全向内的节点(网络的输出端)都只有一个 。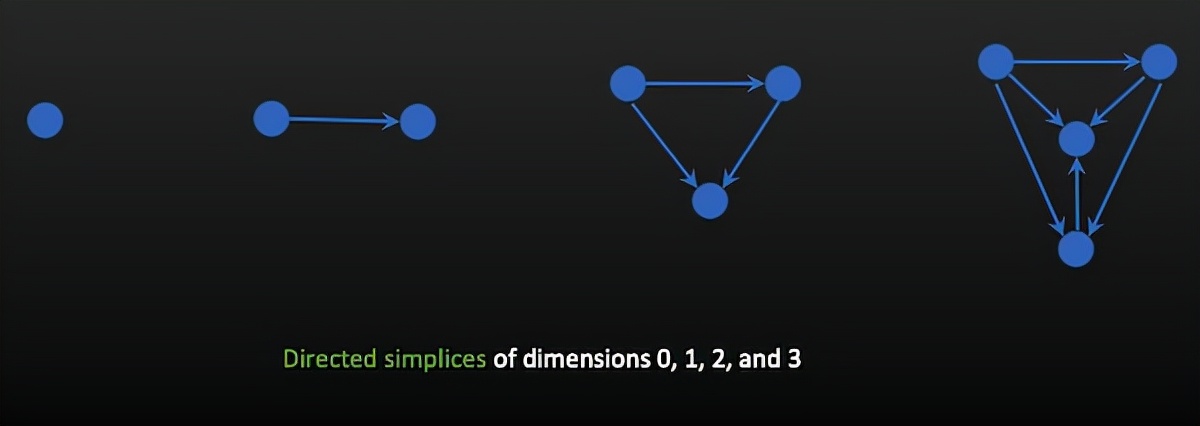
不同维度的有向单纯形丨图片来源:Kathryn Hess
拓扑学的强大之处在于 , 即便只给出局部信息(例如这些神经元的连接方式) , 也能告诉你网络整体的重要特征 。 Hess和她的同事计算了神经元电路中每个维度中有向单纯形的个数 , 并将其与其他可比较类型的的网络进行了局部结构对应数量的比较 。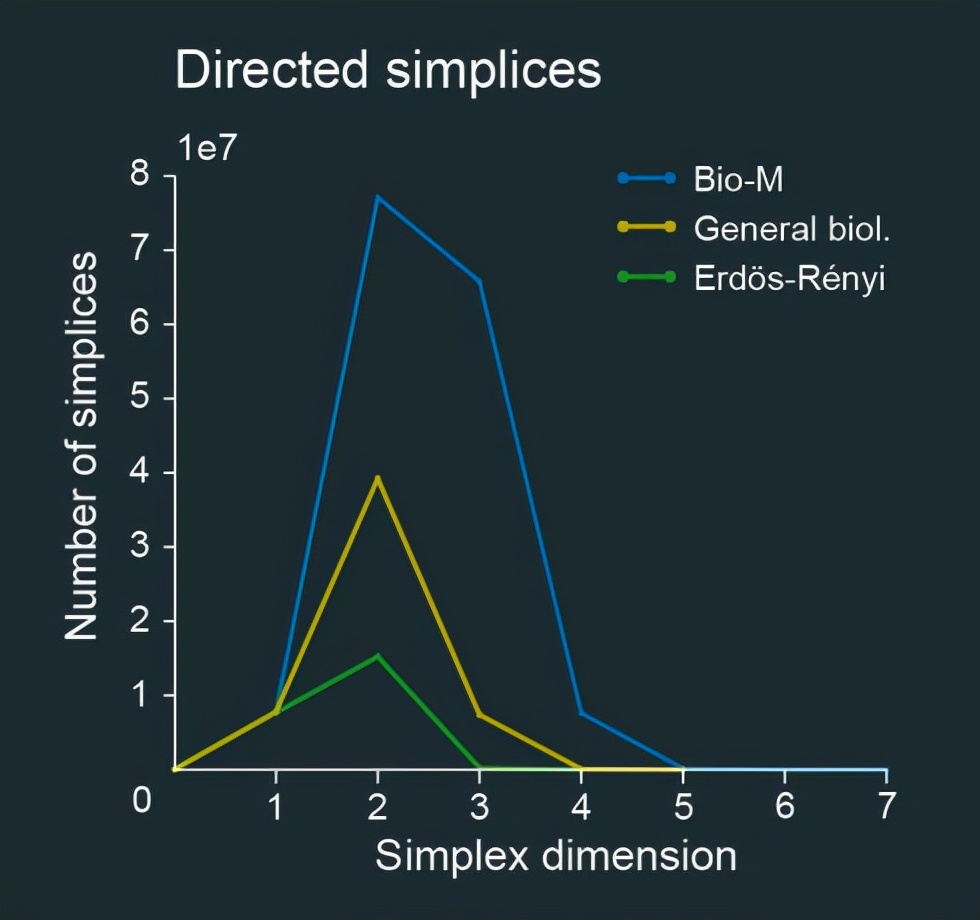
不同维度下的单纯形数量 , 蓝色代表“蓝脑计划”的微型电路;绿色代表随机网络;黄色代表更为一般的生物网络 。 图片来源:Kathryn Hess
他们构造了一种随机网络(图中的绿线) , 从任何一组数量相近的结点开始 , 随机地往外连线 , 使网络中边的数量保持一定 , 连接每个节点的边数也保持一定 , 这与神经微电路相似 。 在这种网络中 , 有向单纯形的数量非常少 , 而且没有维数在4以上的单纯形 。 他们发现 , 在更为一般的生物网络中(不考虑神经元的形状大小) , 也存在这种现象 。
重建出的神经元微型电路中 , 有向单纯形的数量却比其他网络中高得多 , 而且还包括高维有向单纯形 。 Hess表示 , “蓝脑计划”中的微型电路有更多(数量) , 该电路与随机网络相去甚远 。 ”他们的研究结果表示 , 为了使神经元必要的传导行为能够协调……这些神经元必须得属于一个更大的结构(例如这些高维单纯形) 。
推荐阅读
- 核心|中科大陈秀雄团队成功证明凯勒几何两大核心猜想,研究登上《美国数学会杂志》
- 视点·观察|HDMI 2.1a规范或让用户购买HDMI线缆更复杂
- 视点·观察|张庭夫妇实控公司涉嫌传销被调查,加盟商:拉人头、疯狂囤货、盈利机制复杂
- 逻辑|小米张国权:动态刷新率场景非常多、逻辑复杂,将开放 SDK
- 模型|经逆向工程,Transformer「翻译」成数学框架 | 25位学者撰文
- 镜面|韦布望远镜技术细节大公开:有多复杂
- 数学|中考数学阴影部分面积计算方法总结
- 预测|机器学习预测复杂新材料合成
- 处理|我们计划招收300名数学爱好者,免费系统学习Matlab与傅立叶变换
- 问题|第六届“复旦-中植科学奖”授予两位数学家





