神经元网络可以用有向图来表示丨图片来源:Kathryn Hess
重建大脑
Hess与“蓝脑计划(Blue Brain Project)”进行合作 。 “(仿真)人脑模型的规模远远超过了我们力所能及 , ”Hess说道 , “毕竟有数百亿个神经元 , 数据量是无法想象的庞大 。 ”所以为了重建大脑的数学模型 , “蓝脑计划”研究了比人类小得多的大鼠的大脑 。 不过Hess表示 , 即便鼠脑已经很小了 , 他们面对的仍然是“神经元网络的狂野纠缠” 。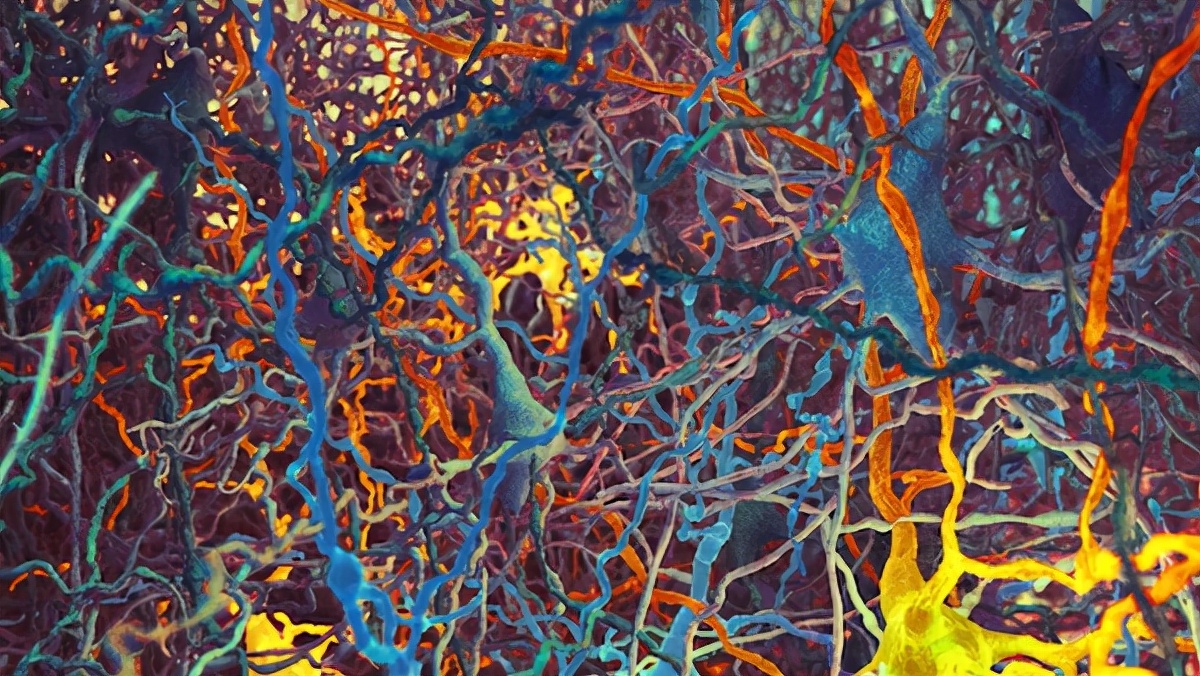
大鼠新皮层中不同类型的神经元缠结的数据可视化图像丨图片来源:Nicolas Antille, EPFL.
在过去的十年中 , “蓝脑计划”重建了鼠脑中的躯体感觉新皮质(somatosensory neocortex)——这就像是从鼠脑表面深入到灰质提取出来一份岩心样本 。 大脑中负责触觉的部分组成一个微型电路 , 这里包括了大约30000个神经元以及它们之间的800万个连接 。 重建的过程 , 首先是在微型电路的柱状区域中安放不同的“神经元” , 来模拟实验室中观察到的种类和数量 。 接下来这些神经元将按照邻近关系以及我们对鼠脑已有的信息来连接 。
用来重建微型电路的算法包含了随机性(stochastic) 。 也就是说 , 算法中的某些分支是依照概率来选择的 , 所以算法每运行一次 , 重建的结果都会不同 。 “蓝脑计划”最开始使用的数据来自五块不同鼠脑 , 和一个汇集了各个大脑数据的“平均”脑 。 接着他们对每个数据集运行了7次重建(7次之间的差别其实不是很大) , 这样就有了总共42个微型电路 。
之后 , 研究人员将突触的电性质编码到微型电路里 , 如此神经元电路就被真正连接起来 , 这样部分鼠脑的重建就完成了 。 “蓝脑计划”的最终目标是用重建的大脑来研究神经系统的失调 , 比如帕金森氏症 , 以及减少药物研发过程中的动物实验 。
揭示结构
拓扑学是数学中研究形状分类的学科 。 如果某个图形可以通过弯曲或拉伸变成另一个图形 , 只要变化过程中没有切断或撕裂 , 我们就认为两个图形相同 。 最著名的例子就是甜甜圈和咖啡杯 , 它们从拓扑意义上来说是一样的 。 如果有一个橡皮泥做的咖啡杯 , 那么你只要把杯身一点点地往杯把的那边挤 , 就可以把它连续地变成甜甜圈 。 在这个变换过程中 , 咖啡杯把手的那个洞始终没有变 , 只是变成了甜甜圈的那个洞——洞是不可能消失的 。 拓扑学对于像洞一样 , 在连续变换下不变的量 , 非常感兴趣 。
推荐阅读
- 核心|中科大陈秀雄团队成功证明凯勒几何两大核心猜想,研究登上《美国数学会杂志》
- 视点·观察|HDMI 2.1a规范或让用户购买HDMI线缆更复杂
- 视点·观察|张庭夫妇实控公司涉嫌传销被调查,加盟商:拉人头、疯狂囤货、盈利机制复杂
- 逻辑|小米张国权:动态刷新率场景非常多、逻辑复杂,将开放 SDK
- 模型|经逆向工程,Transformer「翻译」成数学框架 | 25位学者撰文
- 镜面|韦布望远镜技术细节大公开:有多复杂
- 数学|中考数学阴影部分面积计算方法总结
- 预测|机器学习预测复杂新材料合成
- 处理|我们计划招收300名数学爱好者,免费系统学习Matlab与傅立叶变换
- 问题|第六届“复旦-中植科学奖”授予两位数学家








