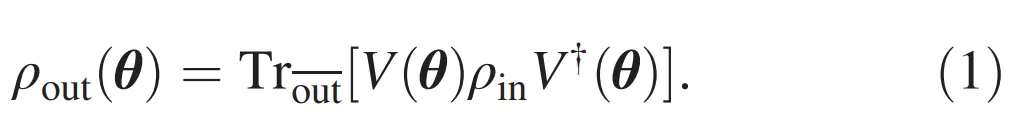
文章图片
其中 , V(θ)是包含卷积层和池化层以及全连接层中的门的 unitary , θ 是可训练参数的向量 ,
文章图片
表示除 H_out 中以外的所有量子比特的偏迹数(partial trace) 。 请注意 , QCNN 中的非线性源于池化层中的池化算子 , 这有效地降低了每一层的自由度 。
代价函数
QCNN 的目标是应用一个训练集 S(S 的大小 M=|S|) , 包含输入状态
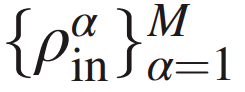
文章图片
来优化 QCNN 中的参数 , 并最小化代价函数 , 代价函数可表示为
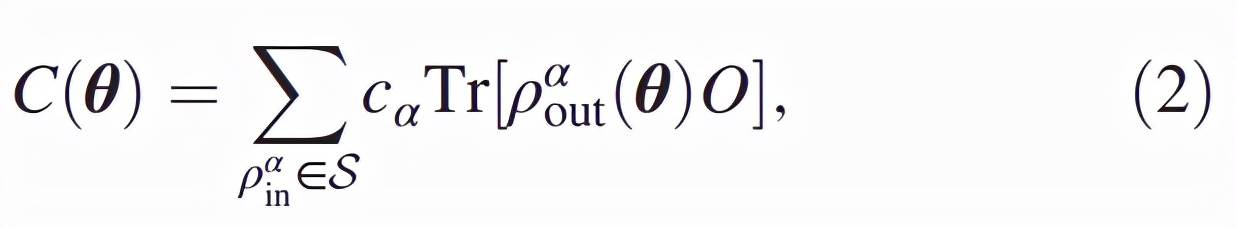
文章图片
其中 c_α是实系数 ,

文章图片
是从如下等式 (1) 中获得的 , 每个输入状态为ρ_in 。
Ansatz
为了简单起见 , 该研究主要考虑两种情况:n=2^k 和 L=log(n)=k , 这样 dim(H_out)=2 。 此外 , 该研究假设卷积层和池化层中的 unitary 是独立的 。 也就是说 , V(θ) 中的卷积层和全连接层由作用于相邻量子比特的两个量子比特参数化 unitary 块组成 , 表示为
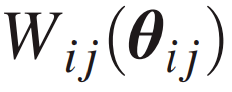
文章图片
。
研究者注意到 , 这种泛化包含作为特殊情况的常见 QCNN 结构 , 其中同一卷积或池化层中的块是相同的 。 此外 , 研究者在论文的结果部分讨论得出:卷积层中的 unitary 相关性往往会增加代价函数的梯度幅值 。
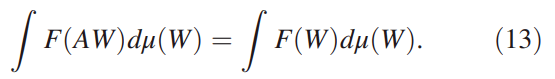
文章图片
如上等式 (13) 所示 , 由于代价函数偏导数的方差独立于 I_ij 中的受控 unitary , 因此可以将池化层中算子 I_ij 的作用附到卷积层中 unitary 的作用上 。 因此 , QCNN 的张量网络表征如下图 2 所示 。
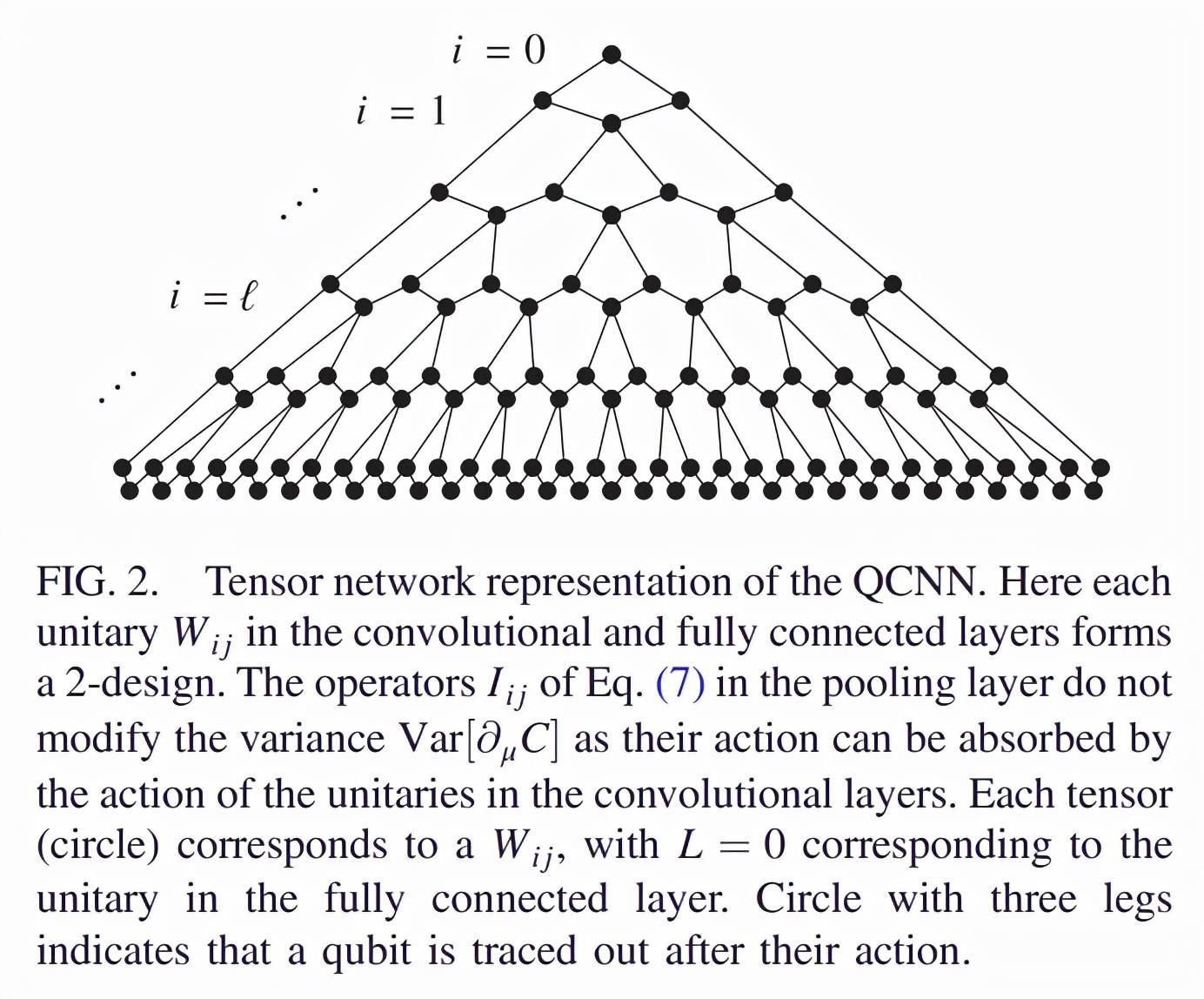
文章图片
QCNN 的张量网络表征 。
此外 , 该研究还提出了一种分析方差缩放的新方法 , 称为 GRIM 。
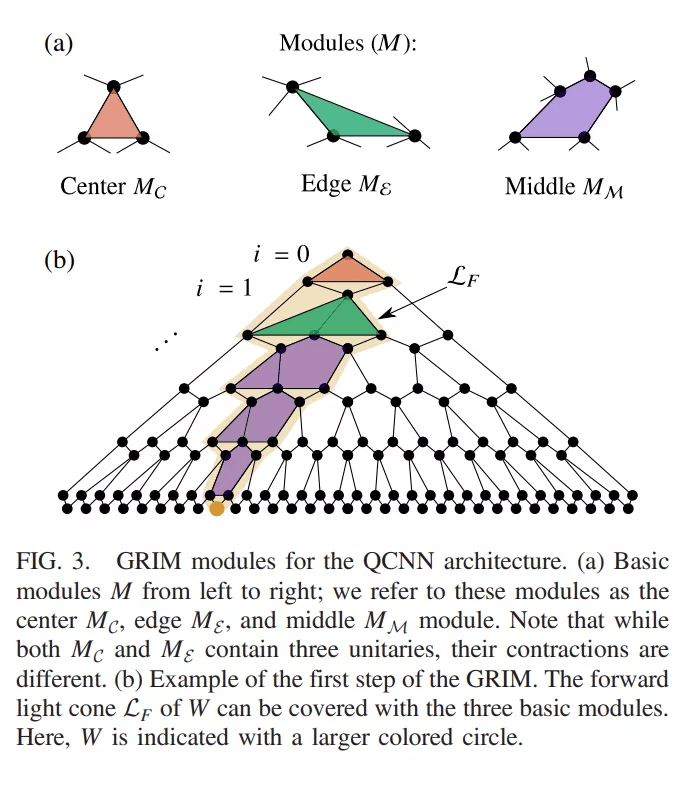
文章图片
QCNN 架构的 GRIM 模块 。
这项研究有什么意义?
作为一种人工智能方法 , QCNN 受到视觉皮层的启发 , 因此涉及一系列的卷积层与池化层 , 在保持数据集重要特征的同时降低了数据的维度 。 这些神经网络可用于解决一系列问题 , 从图像识别到材料发现 。 克服贫瘠高原是挖掘量子计算机在人工智能应用中的全部潜力并展示其优于经典计算机的关键 。
推荐阅读
- 网络|天津联通全力助推天津市入选全国首批千兆城市
- 网络化|工信部:2025年建成500个以上智能制造示范工厂
- 视点·观察|张庭夫妇公司被查 该怎样精准鉴别网络传销?
- 最新消息|宝马LG和其他公司正考虑使用量子计算机解决具体问题
- 器件|6G、量子计算、元宇宙…上海市“十四五”聚焦这些前沿领域
- 前瞻|6G、量子计算、元宇宙……上海市“十四五”聚焦这些前沿新兴领域
- 数字化|70%规模以上制造业企业到2025年将实现数字化、网络化
- 人物|俄罗斯网络博主为吸引流量 闹市炸毁汽车 结果够“刑”
- 协同|网文论︱网络文学与AI写作:人机协同演化时代的文学之灵
- 周鸿祎|网络安全行业应提升数字安全认知







