arima|拓端tecdat|R语言arima，向量自回归VAR，周期自回归(PAR)分析温度时间序列_分析|序列|周期|in|检验|单位根

原文链接： http://tecdat.cn/?p=22071
至少有两种非平稳时间序列：具有趋势的时间序列和具有单位根的时间序列（称为单整时间序列）。单位根检验不能用来评估时间序列是否平稳。它们只能检测单整时间序列。季节性单位根也是如此。
这里考虑月平均温度数据。

> mon=read.table("temp.txt")
> plot(mon)

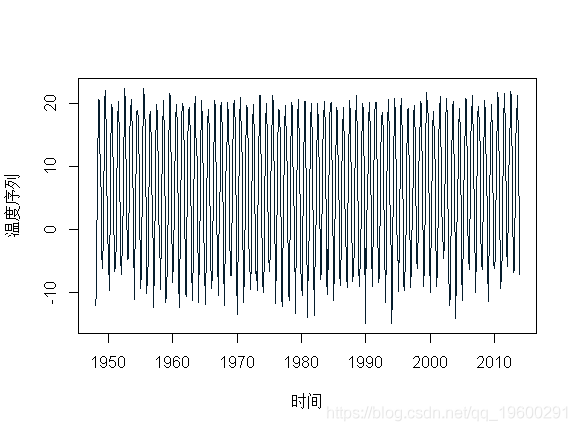
arima|拓端tecdat|R语言arima，向量自回归VAR，周期自回归(PAR)分析温度时间序列

文章图片

现在，我们可以计算所有年份的三个不同平稳性检验的p值

for(y in 1955:2013){
Temp[which(Year==y)]
as.numeric(pp.test(Zc)$p.value)
as.numeric(kpss.test(Zc)$p.value)
as.numeric(adf.test(Zc)$p.value)

从图像上看，如果红色表示非平稳，蓝色表示平稳，我们得到
polygon(y,col=CL[1+(D[y-1954,i]==1)*5],border=NA)}}

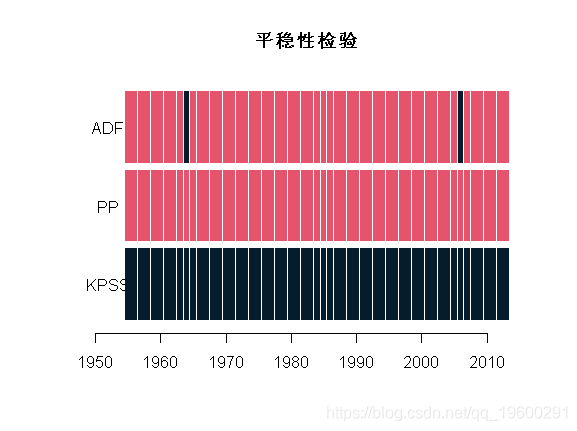
文章图片

可以看到大部分序列在5%显著性水平下无法拒绝原检验说明序列非平稳。
冬天和夏天的温度是完全不同的。我们可以来可视化：

> plot(month,(tsm))
> lines(1:12,apply(M,2,mean

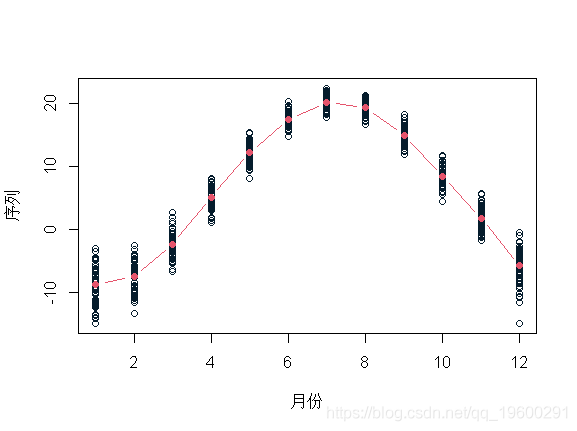
文章图片

或者
plot(tsm)

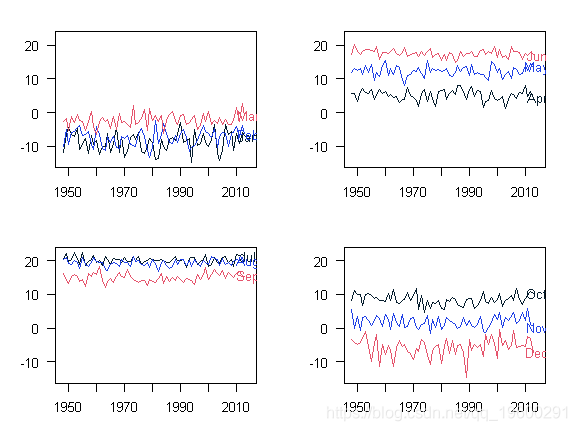
文章图片

> 3D(tsm)

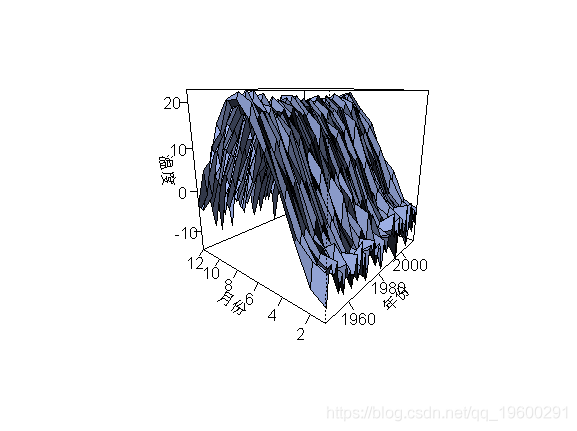
文章图片

看起来我们的时间序列是周期性的，因为每年都是季节性的。自相关函数：

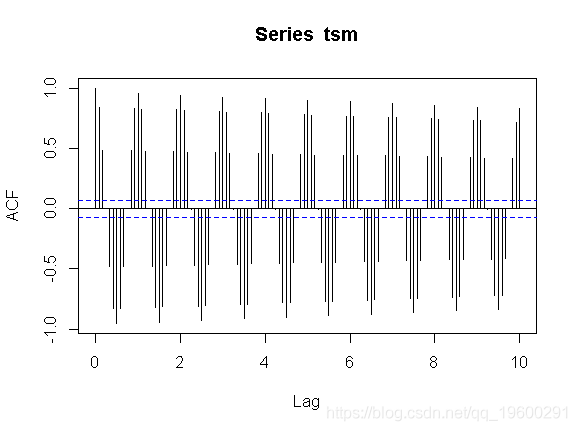
文章图片

现在的问题是有季节性单位根吗?这说明我们的模型应该是

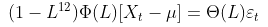
文章图片

如果我们忘记了自回归和移动平均分量，我们可以估计

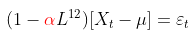
文章图片

如果有季节性单位根，那么应该接近1 。

arima(x = tsm, order = c(0, 0, 0), seasonal = list(order = c(1, 0, 0), period = 12))
Coefficients:
sar1 intercept
0.9702 6.4566
s.e. 0.0071 2.1515

和1差不多。实际上，它不能太接近1 。如果是的话，我们会收到一条错误信息…
为了说明模型，让我们考虑季度温度，
sp(1:4,N,theta=-50,col="yellow",shade=TRUE,

文章图片

VAR季度温度模型 VAR模型描述在同一样本期间内的n个变量（内生变量）可以作为它们过去值的线性函数。
一个VAR(p)模型可以写成为：

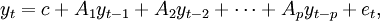
文章图片

其中：c是n × 1常数向量， Ai是n × n矩阵。 et是n × 1误差向量，满足：

—误差项的均值为0

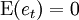
文章图片

—误差项的协方差矩阵为Ω（一个n × 'n正定矩阵）

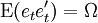
文章图片

（对于所有不为0的k都满足）—误差项不存在自相关

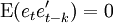
文章图片

其中A是4X4矩阵。这个模型很容易估计
model=VAR(df)

文章图片

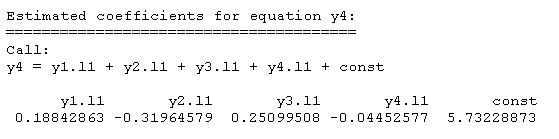
文章图片

矩阵A在这里

> A=rbind(
+ coefficients(varresult$y1)[1:4],
+ coefficients(varresult$y2)[1:4],
+ coefficients(varresult$y3)[1:4],
+ coefficients(varresult$y4)[1:4])

文章图片

由于这个多时间序列的平稳性与这个矩阵的特征值密切相关，我们来看一下，

> eigen(A)
[1] 0.35834830 -0.32824657 -0.14042175 0.09105836
> Mod(eigen(A)
[1] 0.35834830 0.32824657 0.14042175 0.09105836

周期自回归(PAR)模型看起来这里不存在平稳性问题。有限制的模型称为周期自回归模型，被称为模型

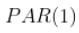
文章图片

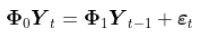
文章图片

其中

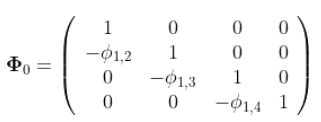
文章图片

并且

文章图片

这是一个VAR(1) 模型，因此

文章图片

可以来估计这个模型

par(wts=tsq, type="PAR", p=1)
> PAR(model)

文章图片

特征方程为

文章图片

所以有一个(季节性的)单位根，如果

文章图片

但在这里显然不是这样。可以进行 Canova Hansen(CH)检验。 Canova Hansen(CH)检验主要用于检验季节差异并验证零假设,即季节性模式在采样期内是稳定的或随时间而变化。
检验的输出在这里
> CH.test(tsm)

文章图片

看起来我们拒绝了季节性单位根的假设。我提到以下检验程序

> nsdiffs(tsm, test="ch")
[1] 0

其中输出:“1”表示有一个季节单位根， “0”表示没有季节单位根。读起来很简单，不是吗?如果我们考虑每月数据的周期自回归模型，输出是
> model

文章图片

所以，不管是什么检验，我们总是拒绝有季节性单位根的假设。这并不意味着我们的序列不能是周期性的！实际上，这个序列几乎是周期性的。但是没有单位根！所以所有这些都是有意义的。
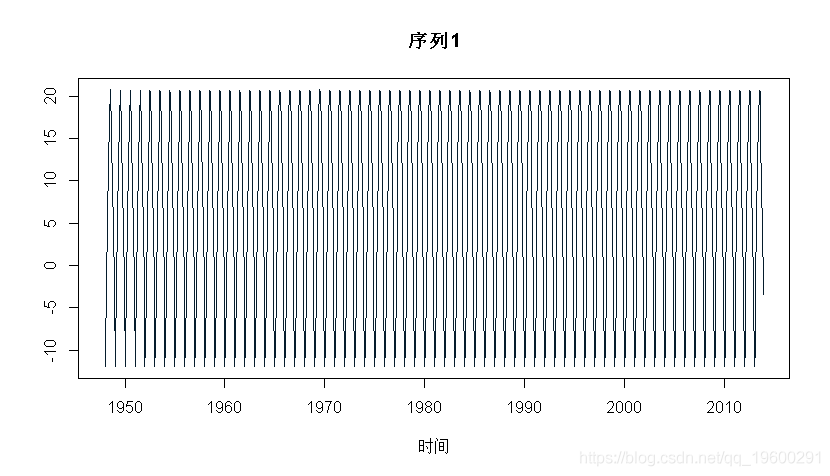
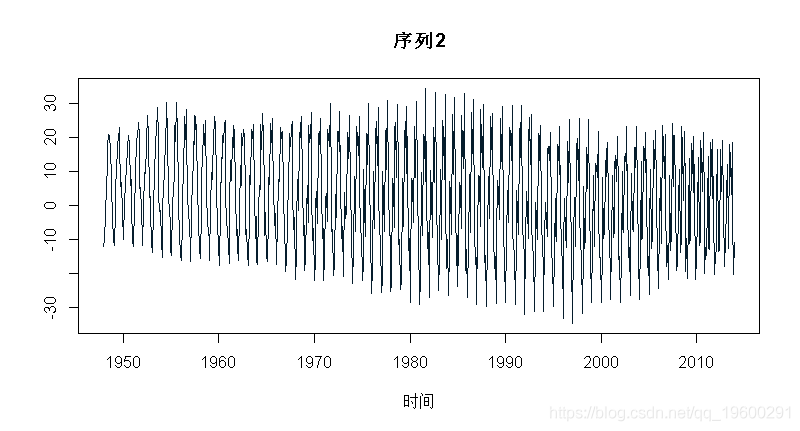
为了确保我们得到的是正确的，考虑两个时间序列。第一个是周期序列(有非常小的噪声) ，第二个是单整序列。

> p1=Xp2=as.numeric(t(M))
> for(t in 13:length(M)){
+ p2[t]=Xp2[t-12]+rnorm(1,0,2)

文章图片

文章图片

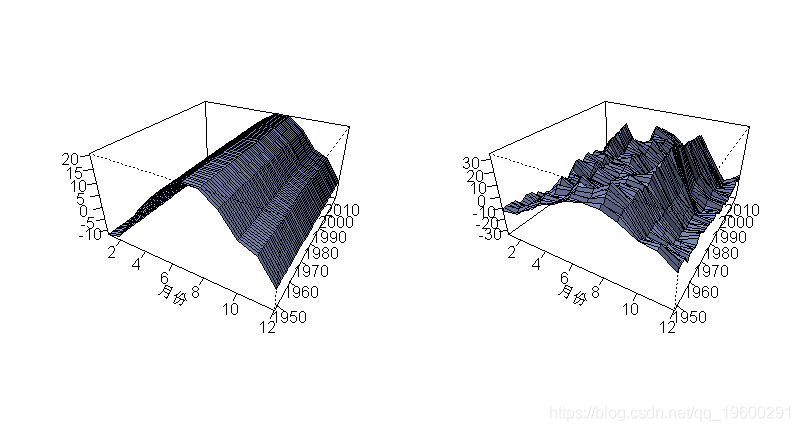
查看

3D(tsp1)
3D(tsp2)

文章图片

如果我们快速地看一下这些序列，我会说第一个没有单位根-即使它不是平稳的，但这是因为这个序列是周期性的-而第二个有单位根。如果我们看一下 Canova Hansen(CH)检验，我们会得到
> CH.test(tsp1)

文章图片

文章图片

考虑一下

> nsdiffs(tsp1, 12,test="ch")
[1] 0
> nsdiffs(tsp2, 12,test="ch")
[1] 1

这里我们有相同的结论。第一个没有单位根，但是第二个有单位根。用Osborn-Chui-Smith-Birchenhall检验

> nsdiffs(tsp1, 12,test="ocsb")
[1] 1
> nsdiffs(tsp2, 12,test="ocsb")
[1] 1

在我们的周期序列中也有一个单位根。
所以在这里，在低频上，我们拒绝在我们的温度序列中有单位根的假设，甚至是季节性的单位根。

文章图片

最受欢迎的见解
1.在python中使用lstm和pytorch进行时间序列预测
2.python中利用长短期记忆模型lstm进行时间序列预测分析
3.使用r语言进行时间序列（arima ，指数平滑）分析
4.r语言多元copula-garch-模型时间序列预测
5.r语言copulas和金融时间序列案例
6.使用r语言随机波动模型sv处理时间序列中的随机波动
7.r语言时间序列tar阈值自回归模型
8.r语言k-shape时间序列聚类方法对股票价格时间序列聚类
【arima|拓端tecdat|R语言arima，向量自回归VAR，周期自回归(PAR)分析温度时间序列】9.python3用arima模型进行时间序列预测