Copula|拓端tecdat|R语言Copula函数股市相关性建模：模拟Random Walk(随机游走)_相关性|函数|股市|Walk|模拟|R

原文链接：http://tecdat.cn/?p=19688
在引入copula时，大家普遍认为copula很有趣，因为它们允许分别对边缘分布和相依结构进行建模。
copula建模边缘和相依关系给定一些边缘分布函数和一个copula ，那么我们可以生成一个多元分布函数，其中的边缘是前面指定的。
考虑一个二元对数正态分布

> library(mnormt)
> set.seed(1)
> Z=exp(rmnorm(25,MU,SIGMA))

我们可以从边缘分布开始。

meanlog sdlog
1.168 0.930
(0.186 ) (0.131 )
meanlog sdlog
2.218 1.168
(0.233 ) (0.165 )

基于这些边缘分布，并考虑从该伪随机样本获得的copula参数的最大似然估计值，从数值上讲，我们得到

> library(copula)
> Copula() estimation based on 'maximum likelihood'
and a sample of size 25.
Estimate Std. Error z value Pr(>|z|)
rho.1 0.86530 0.03799 22.77

但是，由于相依关系是边缘分布的函数，因此我们没有对相依关系进行单独处理。如果考虑全局优化问题，则结果会有所不同。可以得出密度

> optim(par=c(0,0,1,1,0),fn=LogLik)$par
[1] 1.165 2.215 0.923 1.161 0.864

差别不大，但估计量并不相同。从统计的角度来看，我们几乎无法分别处理边缘和相依结构。我们应该记住的另一点是，边际分布可能会错误指定。例如，如果我们假设指数分布，

fitdistr(Z[,1],"exponential")
rate
0.222
(0.044 )
fitdistr(Z[,2],"exponential"
rate
0.065
(0.013 )

高斯copula的参数估计

Copula() estimation based on 'maximum likelihood'
and a sample of size 25.
Estimate Std. Error z value Pr(>|z|)
rho.1 0.87421 0.03617 24.17 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
The maximized loglikelihood is 15.4
Optimization converged

由于我们错误地指定了边缘分布，因此我们无法获得统一的边缘。如果我们使用上述代码生成大小为500的样本，

barplot(counts, axes=FALSE,col="light blue"

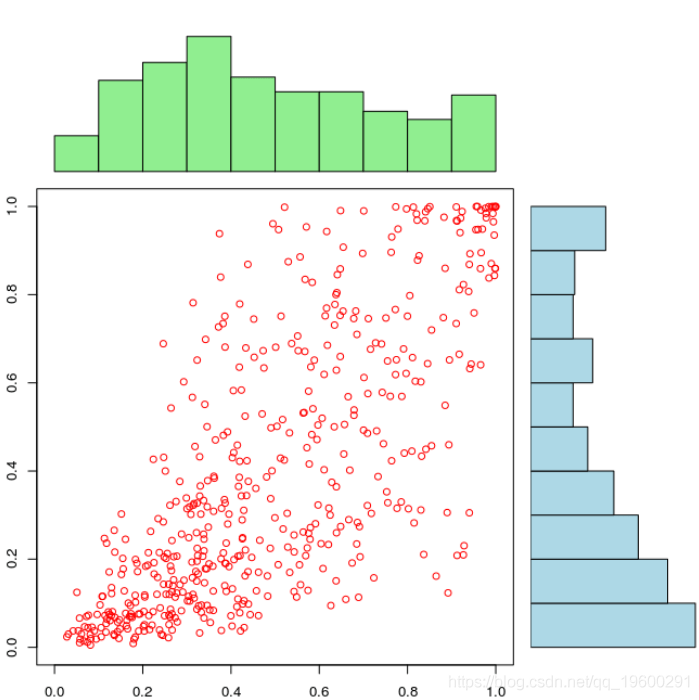
Copula|拓端tecdat|R语言Copula函数股市相关性建模：模拟Random Walk(随机游走)

文章图片

如果边缘分布被很好地设定时，我们可以清楚地看到相依结构依赖于边缘分布，

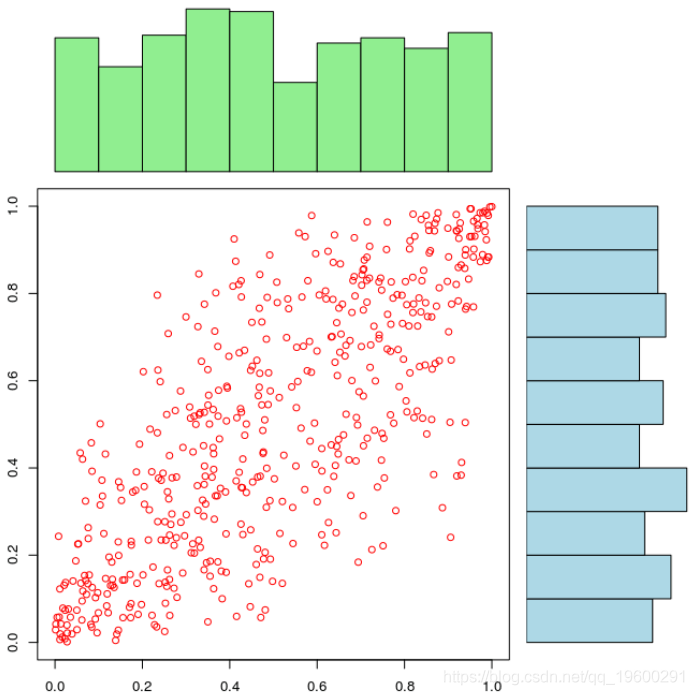
文章图片

copula模拟股市中相关随机游走接下来我们用copula函数模拟股市中的相关随机游走

#*****************************************************************
# 载入历史数据
#******************************************************************
load.packages('quantmod')
data$YHOO = getSymbol.intraday.google('YHOO', 'NASDAQ', 60, '15d')
data$FB = getSymbol.intraday.google('FB', 'NASDAQ', 60, '15d')
bt.prep(data, align='remove.na')
#*****************************************************************
# 生成模拟
#******************************************************************
rets = diff(log(prices))
# 绘制价格
matplot(exp(apply(rets,2,cumsum)), type='l')

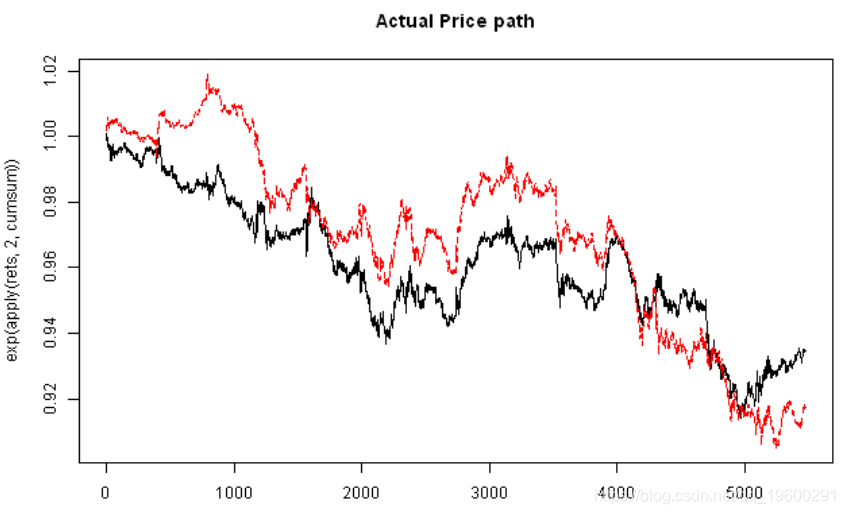
文章图片

# 可视化分布的辅助函数
# 检查Copula拟合的Helper函数
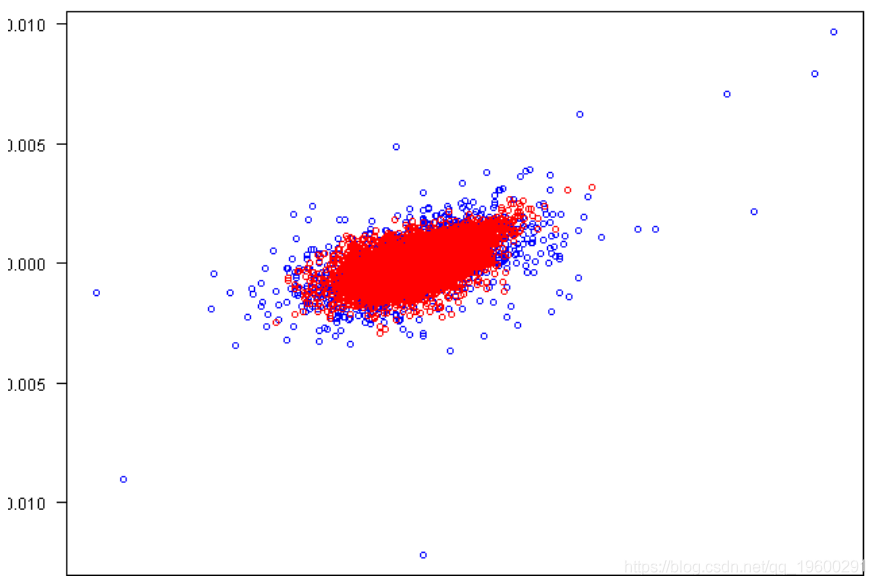
# 模拟图与实际图
plot(rets[,1], rets[,2], xlab=labs[1], ylab=labs[2], col='blue', las=1)
points(fit.sim[,1], fit.sim[,2], col='red')
# 比较模拟和实际的统计数据
temp = matrix(0,nr=5,nc=2)
print(round(100*temp,2))
# 检查收益率是否来自相同的分布
for (i in 1:2) {
print(labs[i])
print(ks.test(rets[,i], fit.sim[i]))
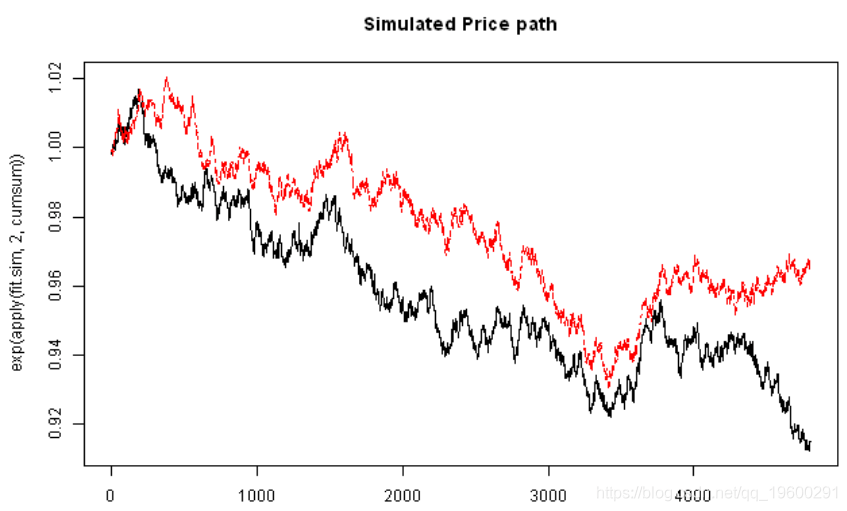
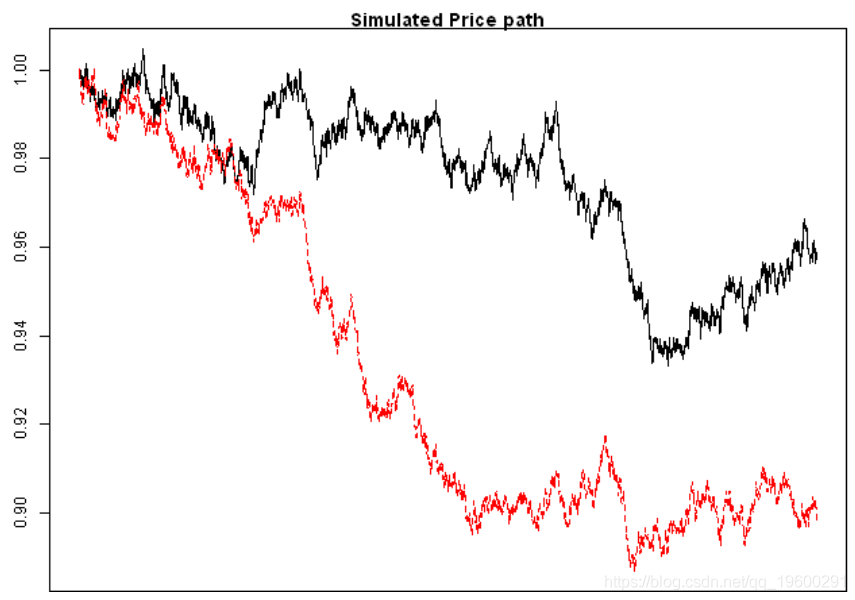
# 绘制模拟价格路径
matplot(exp(apply(fit.sim,2,cumsum)), type='l', main='Simulated Price path')
# 拟合Copula
load.packages('copula')
# 通过组合拟合边缘和拟合copula创建自定义分布
margins=c("norm","norm")
apply(rets,2,function(x) list(mean=mean(x), sd=sd(x)))
# 从拟合分布模拟
rMvdc(4800, fit)

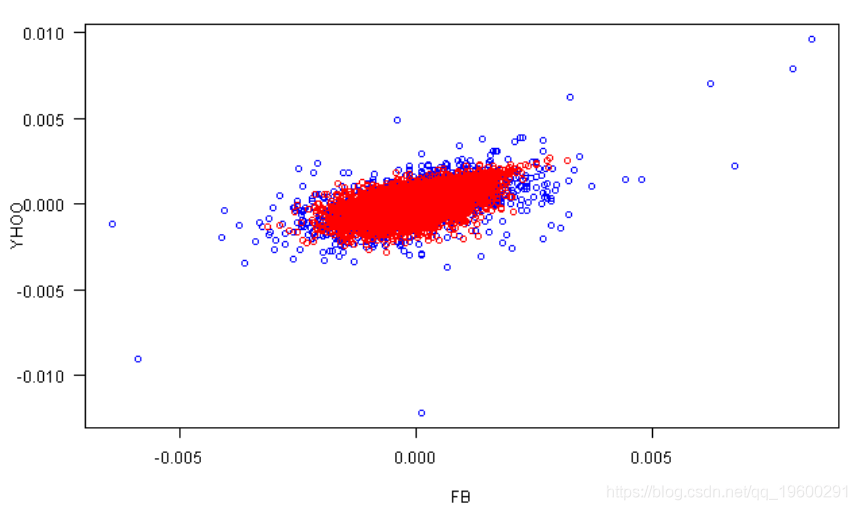
文章图片

Actual Simulated
Correlation 57.13 57.38
Mean FB -0.31 -0.47
Mean YHOO -0.40 -0.17
StDev FB 1.24 1.25
StDev YHOO 1.23 1.23

Two-sample Kolmogorov-Smirnov test
data: rets[, i] and fit.sim[i]
D = 0.9404, p-value = https://www.sohu.com/a/0.3395
alternative hypothesis: two-sided

Two-sample Kolmogorov-Smirnov test
data: rets[, i] and fit.sim[i]
D = 0.8792, p-value = https://www.sohu.com/a/0.4222
alternative hypothesis: two-sided

文章图片

visualize.rets(fit.sim)

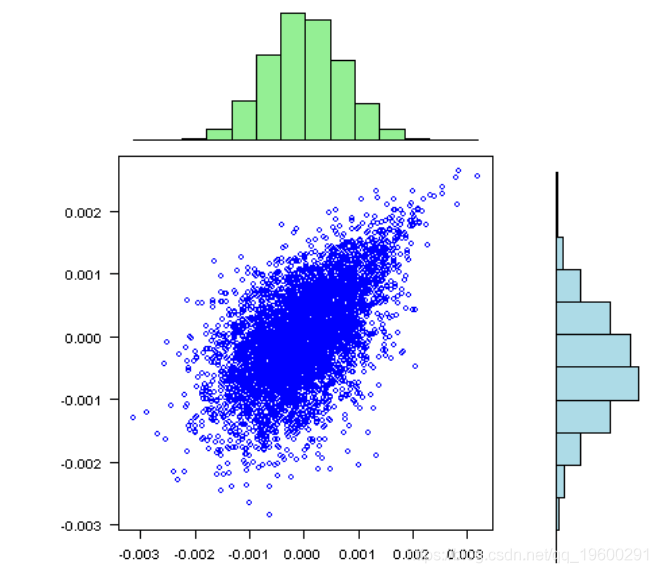
文章图片

# qnorm(runif(10^8)) 和 rnorm(10^8) 是等价的
uniform.sim = rCopula(4800, gumbelCopula(gumbel@estimate, dim=n))

文章图片

Actual Simulated
Correlation 57.13 57.14
Mean FB -0.31 -0.22
Mean YHOO -0.40 -0.56
StDev FB 1.24 1.24
StDev YHOO 1.23 1.21

Two-sample Kolmogorov-Smirnov test
data: rets[, i] and fit.sim[i]
D = 0.7791, p-value = https://www.sohu.com/a/0.5787
alternative hypothesis: two-sided

Two-sample Kolmogorov-Smirnov test
data: rets[, i] and fit.sim[i]
D = 0.795, p-value = https://www.sohu.com/a/0.5525
alternative hypothesis: two-sided

文章图片

文章图片

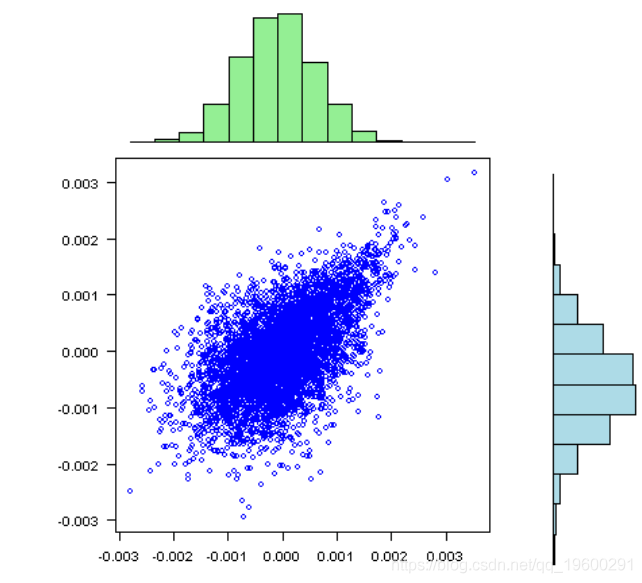
vis(rets)

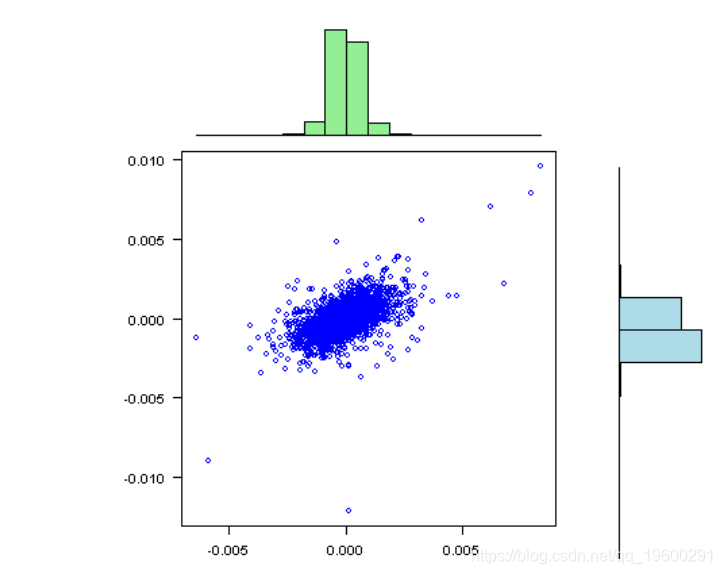
文章图片

标准偏差相对于均值而言非常大，接近于零；因此，在某些情况下，我们很有可能获得不稳定的结果。

文章图片

最受欢迎的见解
1.R语言基于ARMA-GARCH-VaR模型拟合和预测实证研究
2.r语言实现copula算法建模依赖性案例
3.R语言COPULAS和金融时间序列数据VaR分析
4.R语言多元COPULA GARCH 模型时间序列预测
5.GARCH（1,1）， MA以及历史模拟法的VaR比较
6.matlab使用Copula仿真优化市场风险数据分析
7.R语言实现向量自动回归VAR模型
8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型
【Copula|拓端tecdat|R语言Copula函数股市相关性建模：模拟Random Walk(随机游走)】9.R语言VAR模型的不同类型的脉冲响应分析