原文链接：http://tecdat.cn/?p=19405
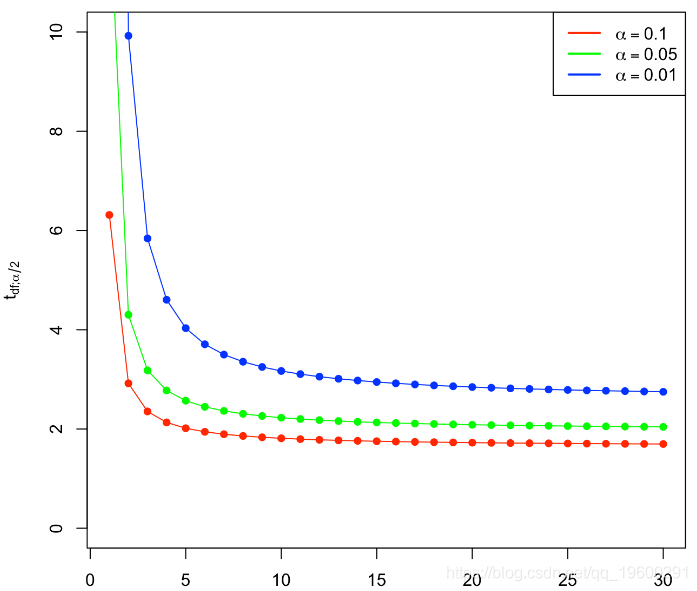
包含更多的预测变量不是免费的：在系数估算的更多可变性 ， 更难的解释以及可能包含高度依赖的预测变量方面要付出代价 。 确实 ，对于样本大小 ， 在线性模型中可以考虑 的预测变量最大数量为 p。 或等效地 ， 使用预测变量p 拟合模型需要最小样本量 。


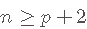
文章图片



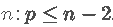
文章图片

如果我们考虑p = 1 和 p = 2 的几何 ， 这一事实的解释很简单：

• 如果p = 1 ， 则至少需要n = 2个点才能唯一地拟合一条线 。 但是 ， 这条线没有给出关于其周围变化的信息 ， 因此无法估计 。 因此 ， 我们至少需要个点 ， 换句话说就是 。

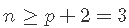
文章图片



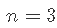
文章图片



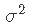
文章图片

• 如果p = 2， 则至少需要n = 3个点才能唯一地拟合平面 。 但是同样 ， 该平面没有提供有关其周围数据变化的信息 ， 因此无法估计 。 因此 ， 我们需要 。

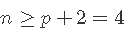
文章图片



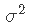
文章图片

下一部分代码的输出阐明了和之间的区别 。


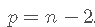
文章图片



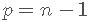
文章图片

2. # 数据：n个观测值 ， p = n-1个预测变量
4. n <- 5
5. p <- n - 1
6. df <- data.frame(y = rnorm(n), x = matrix(rnorm(n * p), nrow = n, ncol = p))
8. # 情况p = n-1 = 2：可以估计beta ， 但不能估计sigma ^ 2（因此 ， 不能执行推断 ， 因为它需要估计的sigma ^ 2）
11. summary(lm(y ~ ., data = https://www.sohu.com/a/df))
13. # 情况p = n-2 = 1：可以估计beta和sigma ^ 2（因此可以进行推断）
15. summary(lm(y ~ . - x.1, data = https://www.sohu.com/a/df))

当减小时 ， 自由度量化的变异性的增加 。


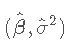
文章图片



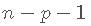
文章图片



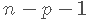
文章图片



文章图片

既然我们已经更多地了解了预测变量过多的问题 ， 我们将重点放在 为多元回归模型选择最合适的预测变量上 。 如果没有独特的解决方案 ， 这将是一项艰巨的任务 。 但是 ， 有一个行之有效的程序通常会产生良好的结果： 逐步模型选择 。 其原理是 依次比较具有不同预测变量的多个线性回归模型 。
在介绍该方法之前 ， 我们需要了解什么是 信息准则 。 信息标准在模型的适用性与采用的预测变量数量之间取得平衡 。 两个常见标准是 贝叶斯信息标准 （BIC）和 赤池信息标准 （AIC） 。 两者都基于 模型适用性和复杂性之间的平衡：


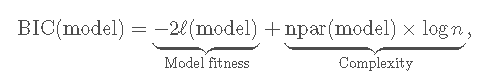
文章图片

其中是模型的对 数似然度 （模型拟合数据的程度） ， 而是考虑的参数数量在模型中 ， 对于具有p个预测变量的多元线性回归模型 ， 则为p + 2 。 AIC在用替换了 ，因此 ， 与BIC相比 ， 它对 较复杂的模型的处罚较少 。 这就是为什么一些从业者更喜欢BIC进行模型比较的原因之一 。 BIC和AIC可以通过BIC 和 计算 AIC 。


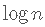
文章图片



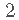
文章图片



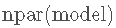
文章图片



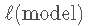
文章图片

我们使用地区房价数据 ， 变量介绍：
（1）town：每一个人口普查区所在的城镇
（2）LON: 人口普查区中心的经度
（3）LAT: 人口普查区中心的纬度
（4）MEDV: 每一个人口普查区所对应的房子价值的中位数 (单位为$1000)
（5）CRIM: 人均犯罪率
（6）ZN: 土地中有多少是地区是大量住宅物业
（7）INDUS: 区域中用作工业用途的土地占比
（8）CHAS: 1：该人口普查区紧邻查尔斯河；0： 该人口普查区没有紧邻查尔斯河
（9）NOX: 空气中氮氧化物的集中度 (衡量空气污染的指标)
（10）RM: 每个房子的平均房间数目
（11）AGE: 建于1940年以前的房子的比例
（12）DIS: 该人口普查区距离波士顿市中心的距离
（13）RAD: 距离重要高速路的远近程度 (1代表最近；24代表最远)
（14）TAX: 房子每$10,000价值所对应的税收金额
（15）PTRATIO: 该城镇学生与老师的比例
他们将作为模型输入 。

1. # 具有不同预测变量的两个模型
3. mod1 <- lm(medv ~ age + crim, data = https://www.sohu.com/a/Boston)
4. mod2 <- lm(medv ~ age + crim + lstat, data = https://www.sohu.com/a/Boston)
5. # BICs
6. BIC(mod1)
7. ## [1] 3581.893
8. BIC(mod2) # 较小->较好
9. ## [1] 3300.841
10. # AICs
11. AIC(mod1)
12. ## [1] 3564.987
13. AIC(mod2) # 较小->较好
14. ## [1] 3279.708
15. # 检查摘要
17. ##
18. ## Residuals:
19. ## Min 1Q Median 3Q Max
20. ## -13.940 -4.991 -2.420 2.110 32.033
21. ##
22. ## Coefficients:
23. ## Estimate Std. Error t value Pr(>|t|)
24. ## (Intercept) 29.80067 0.97078 30.698 < 2e-16 ***
25. ## age -0.08955 0.01378 -6.499 1.95e-10 ***
26. ## crim -0.31182 0.04510 -6.914 1.43e-11 ***
27. ## ---
28. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
29. ##
30. ## Residual standard error: 8.157 on 503 degrees of freedom
31. ## Multiple R-squared: 0.2166, Adjusted R-squared: 0.2134
32. ## F-statistic: 69.52 on 2 and 503 DF, p-value: < 2.2e-16
33. summary(mod2)
34. ##
35. ## Call:
36. ## lm(formula = medv ~ age + crim + lstat, data = https://www.sohu.com/a/Boston)
37. ##
38. ## Residuals:
39. ## Min 1Q Median 3Q Max
40. ## -16.133 -3.848 -1.380 1.970 23.644
41. ##
42. ## Coefficients:
43. ## Estimate Std. Error t value Pr(>|t|)
44. ## (Intercept) 32.82804 0.74774 43.903 < 2e-16 ***
45. ## age 0.03765 0.01225 3.074 0.00223 **
46. ## crim -0.08262 0.03594 -2.299 0.02193 *
47. ## lstat -0.99409 0.05075 -19.587 < 2e-16 ***
48. ## ---
49. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
50. ##
51. ## Residual standard error: 6.147 on 502 degrees of freedom
52. ## Multiple R-squared: 0.5559, Adjusted R-squared: 0.5533
53. ## F-statistic: 209.5 on 3 and 502 DF, p-value: < 2.2e-16

让我们回到预测变量的选择 。 如果我们有p个预测变量 ， 那么一个简单的过程就是检查 所有 可用它们构建的可能模型 ， 然后根据BIC / AIC选择最佳模型 。 这就是所谓的 最佳子集选择 。 问题在于存在个可能的模型！


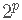
文章图片

让我们看看如何研究 wine 数据集 ， 将使用所有可用预测变量的数据作为初始模型 。
波尔多是法国的葡萄酒产区 。 尽管这种酒的生产方式几乎相同 ， 但已有数百年历史 ， 但每年的价格和质量差异有时非常显着 。 人们普遍认为波尔多葡萄酒陈年越老越好 ， 因此有动力去储存葡萄酒直至成熟 。 主要问题在于 ， 仅通过品尝就很难确定葡萄酒的质量 ， 因为在实际饮用时 ， 味道会发生很大变化 。 这就是为什么葡萄酒品尝师和专家会有所帮助的原因 。 他们品尝葡萄酒 ， 然后预测以后将是最好的葡萄酒 。
1990年3月4日 ， 《纽约时报》宣布普林斯顿大学经济学教授奥利·阿森费尔特（Orley Ashenfelter）可以预测波尔多葡萄酒的质量而无需品尝一滴 。Ashenfelter使用了一种称为线性回归的方法 。 该方法预测结果变量或因变量 。 作为自变量 ， 他使用了酒的年份（因此 ， 较老的酒会更昂贵）和与天气有关的信息 ， 特别是平均生长季节温度 ， 收成雨和冬雨 。
stepAIC 将参数 k 设为2 （默认值）或 ， 其中n是样本大小 。 k = 2 它采用AIC准则 ，k = log(n) 它采用BIC准则 。


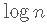
文章图片

1. # 完整模型
3. # 用 BIC
4. ## Start: AIC=-53.29
5. ## Price ~ Year + WinterRain + AGST + HarvestRain + Age + FrancePop
6. ##
7. ##
8. ## Step: AIC=-53.29
9. ## Price ~ Year + WinterRain + AGST + HarvestRain + FrancePop
10. ##
11. ## Df Sum of Sq RSS AIC
12. ## - FrancePop 1 0.0026 1.8058 -56.551
13. ## - Year 1 0.0048 1.8080 -56.519
14. ## <none> 1.8032 -53.295
15. ## - WinterRain 1 0.4585 2.2617 -50.473
16. ## - HarvestRain 1 1.8063 3.6095 -37.852
17. ## - AGST 1 3.3756 5.1788 -28.105
18. ##
19. ## Step: AIC=-56.55
20. ## Price ~ Year + WinterRain + AGST + HarvestRain
21. ##
22. ## Df Sum of Sq RSS AIC
23. ## <none> 1.8058 -56.551
24. ## - WinterRain 1 0.4809 2.2867 -53.473
25. ## - Year 1 0.9089 2.7147 -48.840
26. ## - HarvestRain 1 1.8760 3.6818 -40.612
27. ## - AGST 1 3.4428 5.2486 -31.039
29. summary(modBIC)
30. ##
31. ## Call:
32. ## lm(formula = Price ~ Year + WinterRain + AGST + HarvestRain,
33. ## data = https://www.sohu.com/a/wine)
34. ##
35. ## Residuals:
36. ## Min 1Q Median 3Q Max
37. ## -0.46024 -0.23862 0.01347 0.18601 0.53443
38. ##
39. ## Coefficients:
40. ## Estimate Std. Error t value Pr(>|t|)
41. ## (Intercept) 43.6390418 14.6939240 2.970 0.00707 **
42. ## Year -0.0238480 0.0071667 -3.328 0.00305 **
43. ## WinterRain 0.0011667 0.0004820 2.420 0.02421 *
44. ## AGST 0.6163916 0.0951747 6.476 1.63e-06 ***
45. ## HarvestRain -0.0038606 0.0008075 -4.781 8.97e-05 ***
46. ## ---
47. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
48. ##
49. ## Residual standard error: 0.2865 on 22 degrees of freedom
50. ## Multiple R-squared: 0.8275, Adjusted R-squared: 0.7962
51. ## F-statistic: 26.39 on 4 and 22 DF, p-value: 4.057e-08
52. # 用 AIC
53. ## Start: AIC=-61.07
54. ## Price ~ Year + WinterRain + AGST + HarvestRain + Age + FrancePop
55. ##
56. ##
57. ## Step: AIC=-61.07
58. ## Price ~ Year + WinterRain + AGST + HarvestRain + FrancePop
59. ##
60. ## Df Sum of Sq RSS AIC
61. ## - FrancePop 1 0.0026 1.8058 -63.031
62. ## - Year 1 0.0048 1.8080 -62.998
63. ## <none> 1.8032 -61.070
64. ## - WinterRain 1 0.4585 2.2617 -56.952
65. ## - HarvestRain 1 1.8063 3.6095 -44.331
66. ## - AGST 1 3.3756 5.1788 -34.584
67. ##
68. ## Step: AIC=-63.03
69. ## Price ~ Year + WinterRain + AGST + HarvestRain
70. ##
71. ## Df Sum of Sq RSS AIC
72. ## <none> 1.8058 -63.031
73. ## - WinterRain 1 0.4809 2.2867 -58.656
74. ## - Year 1 0.9089 2.7147 -54.023
75. ## - HarvestRain 1 1.8760 3.6818 -45.796
76. ## - AGST 1 3.4428 5.2486 -36.222
77. summary(modAIC)
78. ##
79. ## Call:
80. ## lm(formula = Price ~ Year + WinterRain + AGST + HarvestRain,
81. ## data = https://www.sohu.com/a/wine)
82. ##
83. ## Residuals:
84. ## Min 1Q Median 3Q Max
85. ## -0.46024 -0.23862 0.01347 0.18601 0.53443
86. ##
87. ## Coefficients:
88. ## Estimate Std. Error t value Pr(>|t|)
89. ## (Intercept) 43.6390418 14.6939240 2.970 0.00707 **
90. ## Year -0.0238480 0.0071667 -3.328 0.00305 **
91. ## WinterRain 0.0011667 0.0004820 2.420 0.02421 *
92. ## AGST 0.6163916 0.0951747 6.476 1.63e-06 ***
93. ## HarvestRain -0.0038606 0.0008075 -4.781 8.97e-05 ***
94. ## ---
95. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
96. ##
97. ## Residual standard error: 0.2865 on 22 degrees of freedom
98. ## Multiple R-squared: 0.8275, Adjusted R-squared: 0.7962
99. ## F-statistic: 26.39 on 4 and 22 DF, p-value: 4.057e-08

接下来是stepAIC 对执行情况的解释。 在每个步骤中 ，stepAIC 显示有关信息标准当前值的信息 。 例如 ， 对于 modBIC ， 第一步的BIC是Step: AIC=-53.29， 然后在第二步进行 了改进 Step: AIC=-56.55 （即使使用“ BIC” ， 该功能也会始终输出“ AIC”） 。 下一个继续前进的模型是stepAIC 通过研究添加或删除预测变量后得出的不同模型的信息标准来决定的 （取决于 direction 参数 ， 在下文中进行解释） 。 例如modBIC在第一步中 ， 删除导致的模型 FrancePop 的BIC等于 -56.551 ， 如果 Year 删除 ， 则BIC将为 -56.519 。 逐步回归 ， 然后删除 FrancePop （因为它给出了最低的BIC） ， 然后重复此过程 ， 最终导致删除 <none> 预测变量是可能的最佳操作 。 下面的代码块说明了stepsAIC的输出 extractAIC ， 和BIC / AIC的输出BIC/ AIC 。

1. # 相同的BIC ， 标准不同
4. AIC(modBIC, k = log(n))
5. ## [1] -56.55135
6. BIC(modBIC)
7. ## [1] 23.36717
8. # 观察到MASS :: stepAIC（mod ， k = log（nrow（wine）））返回的最终BIC是由extractAIC（）而不是BIC（）给出的！但是两者是等效的
9. # 相同的AIC ， 标准不同
12. AIC(modBIC, k = 2)
13. ## [1] -63.03053
14. BIC(modBIC)
15. ## [1] 23.36717
18. BIC(modBIC) - AIC(modBIC
19. ## [1] 79.91852
20. n * (log(2 * pi+ 1) + log(n)
21. ## [1] 79.91852
22. #与AIC相同
25. AIC(modAIC) - AIC(modAIC
26. ## [1] 78.62268
27. n * (log(2 * pi + 1 + 2
28. ## [1] 78.62268

请注意 ， 所选模型 modBIC 和 modAIC 等效于 modWine2， 我们选择的最佳模型 。 这说明 ， 选择的模型 stepAIC 通常是进一步添加或删除预测变量的良好起点 。
使用 stepAIC BIC / AIC时 ， 可能会选择不同的最终模型 direction 。 这是解释：

• “backward”： 从给定模型中顺序删除预测变量 。
• “forward”： 将 预测变量顺序添加到给定模型中 。
• “both” （默认）：以上的组合 。

该 建议 是尝试几种这些方法并保留一个最小的BIC / AIC 。 设置 trace = 0 为省略冗长的搜索过程信息输出 。 下面的代码块清楚地说明了如何使用 数据集的修改版本 来利用 direction 参数和的其他选项。 stepAICwinedirection = "forward"direction = "both"scope

1. # 将无关的预测变量添加到葡萄酒数据集中
2. # 向后选择：从给定模型中顺序删除预测变量
4. # 从具有所有预测变量的模型开始
8. modAll, direction = "backward", k = log(n)
9. ## Start: AIC=-50.13
10. ## Price ~ Year + WinterRain + AGST + HarvestRain + Age + FrancePop +
11. ## noisePredictor
12. ##
13. ##
14. ## Step: AIC=-50.13
15. ## Price ~ Year + WinterRain + AGST + HarvestRain + FrancePop +
16. ## noisePredictor
17. ##
18. ## Df Sum of Sq RSS AIC
19. ## - FrancePop 1 0.0036 1.7977 -53.376
20. ## - Year 1 0.0038 1.7979 -53.374
21. ## - noisePredictor 1 0.0090 1.8032 -53.295
22. ## <none> 1.7941 -50.135
23. ## - WinterRain 1 0.4598 2.2539 -47.271
24. ## - HarvestRain 1 1.7666 3.5607 -34.923
25. ## - AGST 1 3.3658 5.1599 -24.908
26. ##
27. ## Step: AIC=-53.38
28. ## Price ~ Year + WinterRain + AGST + HarvestRain + noisePredictor
29. ##
30. ## Df Sum of Sq RSS AIC
31. ## - noisePredictor 1 0.0081 1.8058 -56.551
32. ## <none> 1.7977 -53.376
33. ## - WinterRain 1 0.4771 2.2748 -50.317
34. ## - Year 1 0.9162 2.7139 -45.552
35. ## - HarvestRain 1 1.8449 3.6426 -37.606
36. ## - AGST 1 3.4234 5.2212 -27.885
37. ##
38. ## Step: AIC=-56.55
39. ## Price ~ Year + WinterRain + AGST + HarvestRain
40. ##
41. ## Df Sum of Sq RSS AIC
42. ## <none> 1.8058 -56.551
43. ## - WinterRain 1 0.4809 2.2867 -53.473
44. ## - Year 1 0.9089 2.7147 -48.840
45. ## - HarvestRain 1 1.8760 3.6818 -40.612
46. ## - AGST 1 3.4428 5.2486 -31.039
47. ##
48. ## Call:
49. ## lm(formula = Price ~ Year + WinterRain + AGST + HarvestRain,
50. ## data = https://www.sohu.com/a/wineNoise)
51. ##
52. ## Coefficients:
53. ## (Intercept) Year WinterRain AGST HarvestRain
54. ## 43.639042 -0.023848 0.001167 0.616392 -0.003861
55. # 从中间模型开始
58. AIC(modInter, direction = "backward", k = log(n)
59. ## Start: AIC=-32.38
60. ## Price ~ noisePredictor + Year + AGST
61. ##
62. ## Df Sum of Sq RSS AIC
63. ## - noisePredictor 1 0.0146 5.0082 -35.601
64. ## <none> 4.9936 -32.384
65. ## - Year 1 0.7522 5.7459 -31.891
66. ## - AGST 1 3.2211 8.2147 -22.240
67. ##
68. ## Step: AIC=-35.6
69. ## Price ~ Year + AGST
70. ##
71. ## Df Sum of Sq RSS AIC
72. ## <none> 5.0082 -35.601
73. ## - Year 1 0.7966 5.8049 -34.911
74. ## - AGST 1 3.2426 8.2509 -25.417
75. ##
76. ## Call:
77. ## lm(formula = Price ~ Year + AGST, data = https://www.sohu.com/a/wineNoise)
78. ##
79. ## Coefficients:
80. ## (Intercept) Year AGST
81. ## 41.49441 -0.02221 0.56067
82. # 回想一下 ， 在搜索过程中未探索未包含在modInter中的其他预测变量（因此未添加相关的预测变量HarvestRain）
85. # 正向选择：从给定模型顺序添加预测变量
87. # 从没有预测变量的模型开始 ， 仅截距模型（表示为?1）
90. AIC(modZero, direction = "forward"
91. ## Start: AIC=-22.28
92. ## Price ~ 1
93. ##
94. ## Df Sum of Sq RSS AIC
95. ## + AGST 1 4.6655 5.8049 -34.911
96. ## + HarvestRain 1 2.6933 7.7770 -27.014
97. ## + FrancePop 1 2.4231 8.0472 -26.092
98. ## + Year 1 2.2195 8.2509 -25.417
99. ## + Age 1 2.2195 8.2509 -25.417
100. ## <none> 10.4703 -22.281
101. ## + WinterRain 1 0.1905 10.2798 -19.481
102. ## + noisePredictor 1 0.1761 10.2942 -19.443
103. ##
104. ## Step: AIC=-34.91
105. ## Price ~ AGST
106. ##
107. ## Df Sum of Sq RSS AIC
108. ## + HarvestRain 1 2.50659 3.2983 -46.878
109. ## + WinterRain 1 1.42392 4.3809 -39.214
110. ## + FrancePop 1 0.90263 4.9022 -36.178
111. ## + Year 1 0.79662 5.0082 -35.601
112. ## + Age 1 0.79662 5.0082 -35.601
113. ## <none> 5.8049 -34.911
114. ## + noisePredictor 1 0.05900 5.7459 -31.891
115. ##
116. ## Step: AIC=-46.88
117. ## Price ~ AGST + HarvestRain
118. ##
119. ## Df Sum of Sq RSS AIC
120. ## + FrancePop 1 1.03572 2.2625 -53.759
121. ## + Year 1 1.01159 2.2867 -53.473
122. ## + Age 1 1.01159 2.2867 -53.473
123. ## + WinterRain 1 0.58356 2.7147 -48.840
124. ## <none> 3.2983 -46.878
125. ## + noisePredictor 1 0.06084 3.2374 -44.085
126. ##
127. ## Step: AIC=-53.76
128. ## Price ~ AGST + HarvestRain + FrancePop
129. ##
130. ## Df Sum of Sq RSS AIC
131. ## + WinterRain 1 0.45456 1.8080 -56.519
132. ## <none> 2.2625 -53.759
133. ## + noisePredictor 1 0.00829 2.2542 -50.562
134. ## + Age 1 0.00085 2.2617 -50.473
135. ## + Year 1 0.00085 2.2617 -50.473
136. ##
137. ## Step: AIC=-56.52
138. ## Price ~ AGST + HarvestRain + FrancePop + WinterRain
139. ##
140. ## Df Sum of Sq RSS AIC
141. ## <none> 1.8080 -56.519
142. ## + noisePredictor 1 0.0100635 1.7979 -53.374
143. ## + Year 1 0.0048039 1.8032 -53.295
144. ## + Age 1 0.0048039 1.8032 -53.295
145. ##
146. ## Call:
147. ## lm(formula = Price ~ AGST + HarvestRain + FrancePop + WinterRain,
148. ## data = https://www.sohu.com/a/wineNoise)
149. ##
150. ## Coefficients:
151. ## (Intercept) AGST HarvestRain FrancePop WinterRain
152. ## -5.945e-01 6.127e-01 -3.804e-03 -5.189e-05 1.136e-03
153. # 在进行正向搜索时 ， 充分设置范围参数非常重要！在范围中 ， 您必须定义包含可探索模型集的“最小”（下部）和“最大”（上部）模型 。 如果未提供 ， 则将最大模型用作传递的起始模型（在这种情况下为modZero） ， 而stepAIC将不执行任何搜索
156. #从中间模型开始
159. ## Start: AIC=-32.38
160. ## Price ~ noisePredictor + Year + AGST
161. ##
162. ## Df Sum of Sq RSS AIC
163. ## + HarvestRain 1 2.71878 2.2748 -50.317
164. ## + WinterRain 1 1.35102 3.6426 -37.606
165. ## <none> 4.9936 -32.384
166. ## + FrancePop 1 0.24004 4.7536 -30.418
167. ##
168. ## Step: AIC=-50.32
169. ## Price ~ noisePredictor + Year + AGST + HarvestRain
170. ##
171. ## Df Sum of Sq RSS AIC
172. ## + WinterRain 1 0.47710 1.7977 -53.376
173. ## <none> 2.2748 -50.317
174. ## + FrancePop 1 0.02094 2.2539 -47.271
175. ##
176. ## Step: AIC=-53.38
177. ## Price ~ noisePredictor + Year + AGST + HarvestRain + WinterRain
178. ##
179. ## Df Sum of Sq RSS AIC
180. ## <none> 1.7977 -53.376
181. ## + FrancePop 1 0.0036037 1.7941 -50.135
182. ##
183. ## Call:
184. ## lm(formula = Price ~ noisePredictor + Year + AGST + HarvestRain +
185. ## WinterRain, data = https://www.sohu.com/a/wineNoise)
186. ##
187. ## Coefficients:
188. ## (Intercept) noisePredictor Year AGST HarvestRain WinterRain
189. ## 44.096639 -0.019617 -0.024126 0.620522 -0.003840 ＃回想一下 ， 在搜索期间不会删除modInter中包含的预测变量（因此会保留无关的noisePredictor）
191. ＃两种选择：如果从中间模型开始 ， 则很有用
193. ＃消除了与从中间模型完成的“向后”和“向前”搜索相关的问题
195. ## Start: AIC=-32.38
196. ## Price ~ noisePredictor + Year + AGST
197. ##
198. ## Df Sum of Sq RSS AIC
199. ## + HarvestRain 1 2.7188 2.2748 -50.317
200. ## + WinterRain 1 1.3510 3.6426 -37.606
201. ## - noisePredictor 1 0.0146 5.0082 -35.601
202. ## <none> 4.9936 -32.384
203. ## - Year 1 0.7522 5.7459 -31.891
204. ## + FrancePop 1 0.2400 4.7536 -30.418
205. ## - AGST 1 3.2211 8.2147 -22.240
206. ##
207. ## Step: AIC=-50.32
208. ## Price ~ noisePredictor + Year + AGST + HarvestRain
209. ##
210. ## Df Sum of Sq RSS AIC
211. ## - noisePredictor 1 0.01182 2.2867 -53.473
212. ## + WinterRain 1 0.47710 1.7977 -53.376
213. ## <none> 2.2748 -50.317
214. ## + FrancePop 1 0.02094 2.2539 -47.271
215. ## - Year 1 0.96258 3.2374 -44.085
216. ## - HarvestRain 1 2.71878 4.9936 -32.384
217. ## - AGST 1 2.94647 5.2213 -31.180
218. ##
219. ## Step: AIC=-53.47
220. ## Price ~ Year + AGST + HarvestRain
221. ##
222. ## Df Sum of Sq RSS AIC
223. ## + WinterRain 1 0.48087 1.8058 -56.551
224. ## <none> 2.2867 -53.473
225. ## + FrancePop 1 0.02497 2.2617 -50.473
226. ## + noisePredictor 1 0.01182 2.2748 -50.317
227. ## - Year 1 1.01159 3.2983 -46.878
228. ## - HarvestRain 1 2.72157 5.0082 -35.601
229. ## - AGST 1 2.96500 5.2517 -34.319
230. ##
231. ## Step: AIC=-56.55
232. ## Price ~ Year + AGST + HarvestRain + WinterRain
233. ##
234. ## Df Sum of Sq RSS AIC
235. ## <none> 1.8058 -56.551
236. ## - WinterRain 1 0.4809 2.2867 -53.473
237. ## + noisePredictor 1 0.0081 1.7977 -53.376
238. ## + FrancePop 1 0.0026 1.8032 -53.295
239. ## - Year 1 0.9089 2.7147 -48.840
240. ## - HarvestRain 1 1.8760 3.6818 -40.612
241. ## - AGST 1 3.4428 5.2486 -31.039
242. ##
243. ## Call:
244. ## lm(formula = Price ~ Year + AGST + HarvestRain + WinterRain,
245. ## data = https://www.sohu.com/a/wineNoise)
246. ##
247. ## Coefficients:
248. ## (Intercept) Year AGST HarvestRain WinterRain
249. ## 43.639042 -0.023848 0.616392 -0.003861 0.001167
250. # 正确定义范围也很重要 ， 因为“两个”都求助于“前进”（以及“后退”）
252. #使用完整模型中的默认值实质上会进行向后选择 ， 但允许已删除的预测变量在以后的步骤中再次输入
255. AIC(modAll direction = "both", k = log(n)
256. ## Start: AIC=-50.13
257. ## Price ~ Year + WinterRain + AGST + HarvestRain + Age + FrancePop +
258. ## noisePredictor
259. ##
260. ##
261. ## Step: AIC=-50.13
262. ## Price ~ Year + WinterRain + AGST + HarvestRain + FrancePop +
263. ## noisePredictor
264. ##
265. ## Df Sum of Sq RSS AIC
266. ## - FrancePop 1 0.0036 1.7977 -53.376
267. ## - Year 1 0.0038 1.7979 -53.374
268. ## - noisePredictor 1 0.0090 1.8032 -53.295
269. ## <none> 1.7941 -50.135
270. ## - WinterRain 1 0.4598 2.2539 -47.271
271. ## - HarvestRain 1 1.7666 3.5607 -34.923
272. ## - AGST 1 3.3658 5.1599 -24.908
273. ##
274. ## Step: AIC=-53.38
275. ## Price ~ Year + WinterRain + AGST + HarvestRain + noisePredictor
276. ##
277. ## Df Sum of Sq RSS AIC
278. ## - noisePredictor 1 0.0081 1.8058 -56.551
279. ## <none> 1.7977 -53.376
280. ## - WinterRain 1 0.4771 2.2748 -50.317
281. ## + FrancePop 1 0.0036 1.7941 -50.135
282. ## - Year 1 0.9162 2.7139 -45.552
283. ## - HarvestRain 1 1.8449 3.6426 -37.606
284. ## - AGST 1 3.4234 5.2212 -27.885
285. ##
286. ## Step: AIC=-56.55
287. ## Price ~ Year + WinterRain + AGST + HarvestRain
288. ##
289. ## Df Sum of Sq RSS AIC
290. ## <none> 1.8058 -56.551
291. ## - WinterRain 1 0.4809 2.2867 -53.473
292. ## + noisePredictor 1 0.0081 1.7977 -53.376
293. ## + FrancePop 1 0.0026 1.8032 -53.295
294. ## - Year 1 0.9089 2.7147 -48.840
295. ## - HarvestRain 1 1.8760 3.6818 -40.612
296. ## - AGST 1 3.4428 5.2486 -31.039
297. ##
298. ## Call:
299. ## lm(formula = Price ~ Year + WinterRain + AGST + HarvestRain,
300. ## data = https://www.sohu.com/a/wineNoise)
301. ##
302. ## Coefficients:
303. ## (Intercept) Year WinterRain AGST HarvestRain
304. ## 43.639042 -0.023848 0.001167 0.616392 -0.003861
305. # 省略冗长的输出
308. AIC(modAll, direction = "both", trace = 0
309. ##
310. ## Call:
311. ## lm(formula = Price ~ Year + WinterRain + AGST + HarvestRain,
312. ## data = https://www.sohu.com/a/wineNoise)
313. ##
314. ## Coefficients:
315. ## (Intercept) Year WinterRain AGST HarvestRain
316. ## 43.639042 -0.023848 0.001167 0.616392 -0.003861

对Boston 数据集运行逐步选择， 目的是清楚地了解不同的搜索方向 。 特别：

• "forward" 从 逐步拟合 medv ~ 1开始做 。
• "forward" 从 逐步拟合 medv ~ crim + lstat + age开始做 。
• "both" 从 逐步拟合 medv ~ crim + lstat + age开始做 。
• "both" 从逐步拟合 medv ~ .开始做 。
• "backward" 从逐步拟合 medv ~ .开始做 。

stepAIC 假定数据中不存在 NA（缺失值） 。 建议先删除数据中的缺失值 。 它们的存在可能会导致错误 。 为此 ， 请使用 data = https://www.sohu.com/a/na.omit(dataset) 调用 lm （如果您的数据集为 dataset） 。
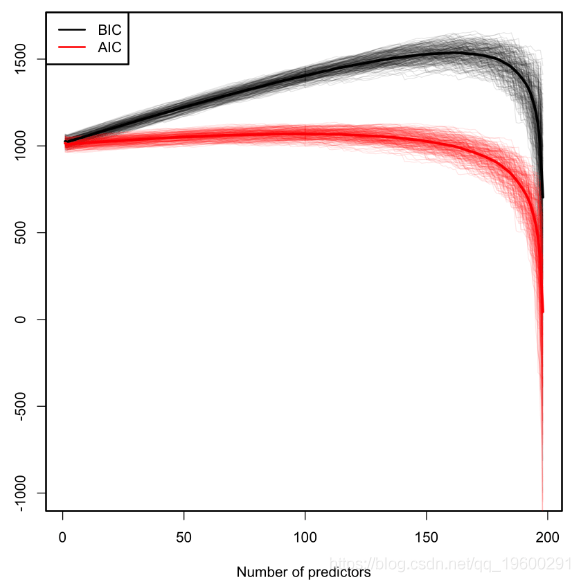
我们通过强调使用BIC和AIC得出结论：它们的构造是假设样本大小n 远大于模型中参数的数量p + 2 。 因此 ， 如果n >> p + 2， 它们将工作得相当好 ， 但是如果不是这样 ， 则它们可能会支持不切实际的复杂模型 。 下图对此现象进行了说明 。 BIC和AIC曲线倾向于使局部最小值接近p = 2 ， 然后增加 。 但是当p + 2 接近n 时 ， 它们会迅速下降 。


文章图片

图：n = 200和p从1 到198 的BIC和AIC的比较 。 M = 100数据集仅在前两个 预测变量有效的情况下进行了模拟。 较粗的曲线是每种颜色曲线的平均值 。
房价案例研究应用 我们要建立一个线性模型进行预测和解释 medv 。 有大量的预测模型 ， 其中一些可能对预测medv没什么用。 但是 ， 目前尚不清楚哪个预测变量可以更好地解释 medv 的信息 。 因此 ， 我们可以对所有 预测变量进行线性模型处理 ：

2. summary(modHouse)
3. ##
4. ##
5. ## Residuals:
6. ## Min 1Q Median 3Q Max
7. ## -15.595 -2.730 -0.518 1.777 26.199
8. ##
9. ## Coefficients:
10. ## Estimate Std. Error t value Pr(>|t|)
11. ## (Intercept) 3.646e+01 5.103e+00 7.144 3.28e-12 ***
12. ## crim -1.080e-01 3.286e-02 -3.287 0.001087 **
13. ## zn 4.642e-02 1.373e-02 3.382 0.000778 ***
14. ## indus 2.056e-02 6.150e-02 0.334 0.738288
15. ## chas 2.687e+00 8.616e-01 3.118 0.001925 **
16. ## nox -1.777e+01 3.820e+00 -4.651 4.25e-06 ***
17. ## rm 3.810e+00 4.179e-01 9.116 < 2e-16 ***
18. ## age 6.922e-04 1.321e-02 0.052 0.958229
19. ## dis -1.476e+00 1.995e-01 -7.398 6.01e-13 ***
20. ## rad 3.060e-01 6.635e-02 4.613 5.07e-06 ***
21. ## tax -1.233e-02 3.760e-03 -3.280 0.001112 **
22. ## ptratio -9.527e-01 1.308e-01 -7.283 1.31e-12 ***
23. ## black 9.312e-03 2.686e-03 3.467 0.000573 ***
24. ## lstat -5.248e-01 5.072e-02 -10.347 < 2e-16 ***
25. ## ---
26. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
27. ##
28. ## Residual standard error: 4.745 on 492 degrees of freedom
29. ## Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338
30. ## F-statistic: 108.1 on 13 and 492 DF, p-value: < 2.2e-16

有几个不重要的变量 ， 但是到目前为止 ， 该模型具有R ^ 2 = 0.74 ， 并且拟合系数对预期的结果很敏感 。 例如 crim ，tax ，ptratio ， 和 nox 对medv有负面影响， 同时 rm ，rad和 chas 有正面的影响 。 但是 ， 不重要的系数不会显着影响模型 ， 而只会增加噪声并降低系数估计的总体准确性 。 让我们稍微完善一下以前的模型 。

1. # 最佳模型
3. AIC(modHouse, k = log(nrow(Boston)
4. ## Start: AIC=1648.81
5. ## medv ~ crim + zn + indus + chas + nox + rm + age + dis + rad +
6. ## tax + ptratio + black + lstat
7. ##
8. ## Df Sum of Sq RSS AIC
9. ## - age 1 0.06 11079 1642.6
10. ## - indus 1 2.52 11081 1642.7
11. ## <none> 11079 1648.8
12. ## - chas 1 218.97 11298 1652.5
13. ## - tax 1 242.26 11321 1653.5
14. ## - crim 1 243.22 11322 1653.6
15. ## - zn 1 257.49 11336 1654.2
16. ## - black 1 270.63 11349 1654.8
17. ## - rad 1 479.15 11558 1664.0
18. ## - nox 1 487.16 11566 1664.4
19. ## - ptratio 1 1194.23 12273 1694.4
20. ## - dis 1 1232.41 12311 1696.0
21. ## - rm 1 1871.32 12950 1721.6
22. ## - lstat 1 2410.84 13490 1742.2
23. ##
24. ## Step: AIC=1642.59
25. ## medv ~ crim + zn + indus + chas + nox + rm + dis + rad + tax +
26. ## ptratio + black + lstat
27. ##
28. ## Df Sum of Sq RSS AIC
29. ## - indus 1 2.52 11081 1636.5
30. ## <none> 11079 1642.6
31. ## - chas 1 219.91 11299 1646.3
32. ## - tax 1 242.24 11321 1647.3
33. ## - crim 1 243.20 11322 1647.3
34. ## - zn 1 260.32 11339 1648.1
35. ## - black 1 272.26 11351 1648.7
36. ## - rad 1 481.09 11560 1657.9
37. ## - nox 1 520.87 11600 1659.6
38. ## - ptratio 1 1200.23 12279 1688.4
39. ## - dis 1 1352.26 12431 1694.6
40. ## - rm 1 1959.55 13038 1718.8
41. ## - lstat 1 2718.88 13798 1747.4
42. ##
43. ## Step: AIC=1636.48
44. ## medv ~ crim + zn + chas + nox + rm + dis + rad + tax + ptratio +
45. ## black + lstat
46. ##
47. ## Df Sum of Sq RSS AIC
48. ## <none> 11081 1636.5
49. ## - chas 1 227.21 11309 1640.5
50. ## - crim 1 245.37 11327 1641.3
51. ## - zn 1 257.82 11339 1641.9
52. ## - black 1 270.82 11352 1642.5
53. ## - tax 1 273.62 11355 1642.6
54. ## - rad 1 500.92 11582 1652.6
55. ## - nox 1 541.91 11623 1654.4
56. ## - ptratio 1 1206.45 12288 1682.5
57. ## - dis 1 1448.94 12530 1692.4
58. ## - rm 1 1963.66 13045 1712.8
59. ## - lstat 1 2723.48 13805 1741.5
60. # 模型比较
61. compare(modBIC, modAIC)
62. ## Calls:
63. ## 1: lm(formula = medv ~ crim + zn + chas + nox + rm + dis + rad + tax + ptratio + black + lstat, data = https://www.sohu.com/a/Boston)
64. ## 2: lm(formula = medv ~ crim + zn + chas + nox + rm + dis + rad + tax + ptratio + black + lstat, data = https://www.sohu.com/a/Boston)
65. ##
66. ## Model 1 Model 2
67. ## (Intercept) 36.34 36.34
68. ## SE 5.07 5.07
69. ##
70. ## crim -0.1084 -0.1084
71. ## SE 0.0328 0.0328
72. ##
73. ## zn 0.0458 0.0458
74. ## SE 0.0135 0.0135
75. ##
76. ## chas 2.719 2.719
77. ## SE 0.854 0.854
78. ##
79. ## nox -17.38 -17.38
80. ## SE 3.54 3.54
81. ##
82. ## rm 3.802 3.802
83. ## SE 0.406 0.406
84. ##
85. ## dis -1.493 -1.493
86. ## SE 0.186 0.186
87. ##
88. ## rad 0.2996 0.2996
89. ## SE 0.0634 0.0634
90. ##
91. ## tax -0.01178 -0.01178
92. ## SE 0.00337 0.00337
93. ##
94. ## ptratio -0.947 -0.947
95. ## SE 0.129 0.129
96. ##
97. ## black 0.00929 0.00929
98. ## SE 0.00267 0.00267
99. ##
100. ## lstat -0.5226 -0.5226
101. ## SE 0.0474 0.0474
102. ##
103. summary(modBIC)
104. ##
105. ## Call:
106. ## lm(formula = medv ~ crim + zn + chas + nox + rm + dis + rad +
107. ## tax + ptratio + black + lstat, data = https://www.sohu.com/a/Boston)
108. ##
109. ## Residuals:
110. ## Min 1Q Median 3Q Max
111. ## -15.5984 -2.7386 -0.5046 1.7273 26.2373
112. ##
113. ## Coefficients:
114. ## Estimate Std. Error t value Pr(>|t|)
115. ## (Intercept) 36.341145 5.067492 7.171 2.73e-12 ***
116. ## crim -0.108413 0.032779 -3.307 0.001010 **
117. ## zn 0.045845 0.013523 3.390 0.000754 ***
118. ## chas 2.718716 0.854240 3.183 0.001551 **
119. ## nox -17.376023 3.535243 -4.915 1.21e-06 ***
120. ## rm 3.801579 0.406316 9.356 < 2e-16 ***
121. ## dis -1.492711 0.185731 -8.037 6.84e-15 ***
122. ## rad 0.299608 0.063402 4.726 3.00e-06 ***
123. ## tax -0.011778 0.003372 -3.493 0.000521 ***
124. ## ptratio -0.946525 0.129066 -7.334 9.24e-13 ***
125. ## black 0.009291 0.002674 3.475 0.000557 ***
126. ## lstat -0.522553 0.047424 -11.019 < 2e-16 ***
127. ## ---
128. ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
129. ##
130. ## Residual standard error: 4.736 on 494 degrees of freedom
131. ## Multiple R-squared: 0.7406, Adjusted R-squared: 0.7348
132. ## F-statistic: 128.2 on 11 and 494 DF, p-value: < 2.2e-16
133. # 置信区间
135. conf(modBIC)
136. ## 2.5 % 97.5 %
137. ## (Intercept) 26.384649126 46.29764088
138. ## crim -0.172817670 -0.04400902
139. ## zn 0.019275889 0.07241397
140. ## chas 1.040324913 4.39710769
141. ## nox -24.321990312 -10.43005655
142. ## rm 3.003258393 4.59989929
143. ## dis -1.857631161 -1.12779176
144. ## rad 0.175037411 0.42417950
145. ## tax -0.018403857 -0.00515209
146. ## ptratio -1.200109823 -0.69293932
147. ## black 0.004037216 0.01454447
148. ## lstat -0.615731781 -0.42937513

请注意 ， 相对于完整模型 ， 略有增加 ， 以及所有预测变量显着 。


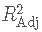
文章图片

我们已经量化了预测变量对房价（Q1）的影响 ， 可以得出结论 ， 在最终模型（Q2）中 ， 显着性水平为 ：


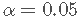
文章图片

• chas ，age ，rad ，black 对medv有 显著正面 的影响 ;
• nox ，dis ，tax ，ptratio ，lstat 对medv有 显著负面 的影响 。

检查：

• modBIC 不能通过消除预测指标来改善BIC 。
• modBIC 无法通过添加预测变量来改进BIC 。 使用 addterm(modBIC, scope = lm(medv ~ ., data = https://www.sohu.com/a/Boston), k = log(nobs(modBIC)))。

1. 应用其公式 ， 我们将获得 ， 因此将不会定义 。

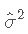
文章图片



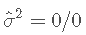
文章图片

1. 具有相同的因变量 。
2. 如果是 ， 则 。

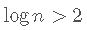
文章图片



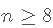
文章图片

1. 同样 ， 由于BIC 在选择真实的分布/回归模型时是 一致的：如果提供了足够的数据 ， 则可以保证BIC在候选列表中选择真实的数据生成模型 。 如果真实模型包含在该列表中 ， 则模型为线性模型 。 但是 ， 由于实际模型可能是非线性的 ， 因此在实践中这可能是不现实的 。

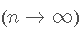
文章图片



文章图片

最受欢迎的见解
1.R语言多元Logistic逻辑回归 应用案例
2.面板平滑转移回归(PSTR)分析案例实现
3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）
4.R语言泊松Poisson回归模型分析案例
5.R语言回归中的Hosmer-Lemeshow拟合优度检验
6.r语言中对LASSO回归 ， Ridge岭回归和Elastic Net模型实现
7.在R语言中实现Logistic逻辑回归
8.python用线性回归预测股票价格
【模型|拓端tecdat|R语言多元逐步回归模型分析房价和葡萄酒价格：选择最合适预测变量】9.R语言如何在生存分析与Cox回归中计算IDI ， NRI指标

推荐阅读

• 

  市面上哪款手机能够算的上是“水桶机”？
• 

  酿魔芋豆腐制作方法 魔芋豆腐酿猪肉的做法步骤
• 

  win7旗舰版支持多大内存 看完这些就清楚了
• 

  照片大小10k什么意思
• 

  请问用于白酒发酵的小曲里面有什么成分啊？
• 

  老三线是什么意思
• 

  带银子发黑是什么原因 银饰变黑的原因
• 

  鲜玫瑰花酱怎么做
• 

  美好的生日祝福语
• 

  蓬莱仙境在哪里
• 

  表示神的词语有哪些
• 

  用户_老陕拍视 迎十四运 西安高新区丈八街道开展志愿者活动
• 

  描写考场气氛的成语
• 

  家暴轻微伤怎么处理
• 

  如何制作简易版紫薯酥饼 紫薯酥饼应该怎么做
• 

  绝对忠诚的动物是什么 忠诚可靠的动物是什么
• 

  床单有黑斑怎么办 如何解决床单有黑斑
• 

  美国GPS为什么只要24颗卫星，北斗却要55颗？看完就知道了
• 

  金牛座男生最配星座 哪个星座和金牛座男生最配
• 

  2022陕西渭南澄城县四价九价约苗指南 陕西渭南澄城县最新消息

• 模型|2022前展望大模型的未来，周志华、唐杰、杨红霞这些大咖怎么看？
• 模型|经逆向工程，Transformer「翻译」成数学框架 | 25位学者撰文
• 化纤|JXK STUDIO 虎年肥猫 1/6仿真动物模型手办可爱摆件
• 模型|达摩院2022十大科技趋势发布：人工智能将催生科研新范式
• 模型|李彦宏:中国迎来AI黄金十年,集度汽车机器人明年亮相,智能交通10年内解决拥堵
• 模型|神经辐射场去掉「神经」，训练速度提升100多倍，3D效果质量不减
• 模型|英伟达：美团机器学习平台使用NVIDIA T4 GPU
• 错误|有了这个工具，不执行代码就可以找PyTorch模型错误
• the|美国大学模型预测：全美未来两月或激增1.4亿确诊
• Samsung|三星Galaxy S22系列模型照片出现 S Pen颜色确认