变量|拓端tecdat|R语言有限混合模型(FMM)及其EM算法聚类分析间歇泉喷发时间_混合|语言|参数|间歇泉|数据

原文链接：http://tecdat.cn/?p=22609
原文出处：拓端数据部落公众号
摘要本文提供了一套用于分析各种有限混合模型的方法。既包括传统的方法，如单变量和多变量正态混合的EM算法，也包括反映有限混合模型的一些最新研究的方法。许多算法都是EM算法或基于类似EM的思想，因此本文包括有限混合模型的EM算法的概述。
1.有限混合模型介绍人群中的个体往往可以被划分为群。然而，即使我们观察到这些个体的特征，我们也可能没有真正观察到这些成员的群体。这项任务在文献中有时被称为 "无监督聚类" ，事实上，混合模型一般可以被认为是由被称为 "基于模型的聚类 "的聚类方法的子集组成。
有限混合模型也可用于那些对个体聚类感兴趣的情况之外。首先，有限混合模型给出了整个子群的描述，而不是将个体分配到这些子群中。有时，有限混合模型只是提供了一种充分描述特定分布的手段，例如线性回归模型中存在异常值的残差分布。
无论建模者在采用混合模型时的目标是什么，这些模型的大部分理论都涉及到一个假设，即子群是按照一个特定的参数形式分布的--而这个形式往往是单变量或多变量正态。
最近的研究目标是放宽或修改多变量正态假设，有限混合模型分析的计算技术，其中的成分是回归、多变量数据离散化产生的向量，甚至是完全未指定的分布。
2. 有限混合模型的EM算法EM算法迭代最大化，而不是观察到的对数似然Lx(θ) ，算式为

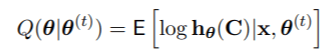
文章图片

1. E步：计算Q(θ|θ(t))
2. M步骤：设定θ(t+1)=argmaxθ∈Φ Q(θ|θ(t))
对于有限混合模型， E步骤不依赖于F的结构，因为缺失数据部分只与Z有关。

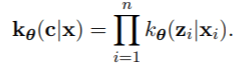
文章图片

Z是离散的，它们的分布是通过贝叶斯定理给出的。 M步骤本身可以分成两部分，与λ有关的最大化，它不依赖于F ，与φ有关的最大化，它必须为每个模型专门处理（例如，参数化、半参数化或非参数化）。因此，模型的EM算法有以下共同特点。
11. E步。计算成分包含的 "后验 "概率（以数据和θ（t）为条件）。

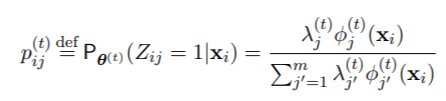
文章图片

对于所有i = 1, . . .， n和j = 1 ，. . . 从数值上看，完全按照公式（2）的写法来实现是很危险的，因为在xi离任何一个成分都很远的情况下，所有的φ（t）j 0（xi）值都会导致数值下溢为零，所以可能会出现不确定的形式0/0 。因此，许多例程实际上使用的是等价表达式

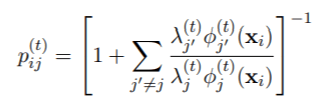
文章图片

或其某种变体。
2. λ的M步骤。设

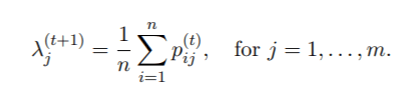
文章图片

2.3. 一个EM算法的例子
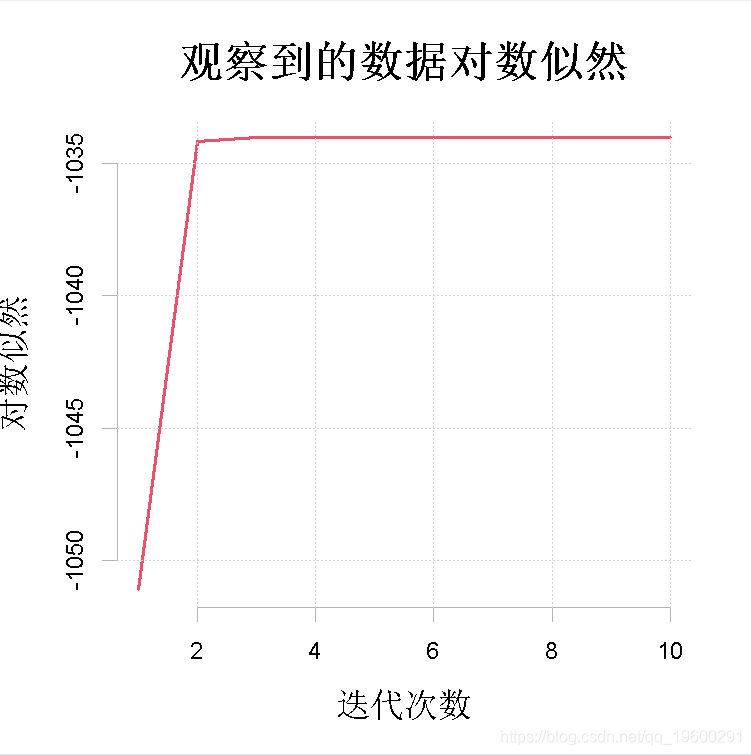
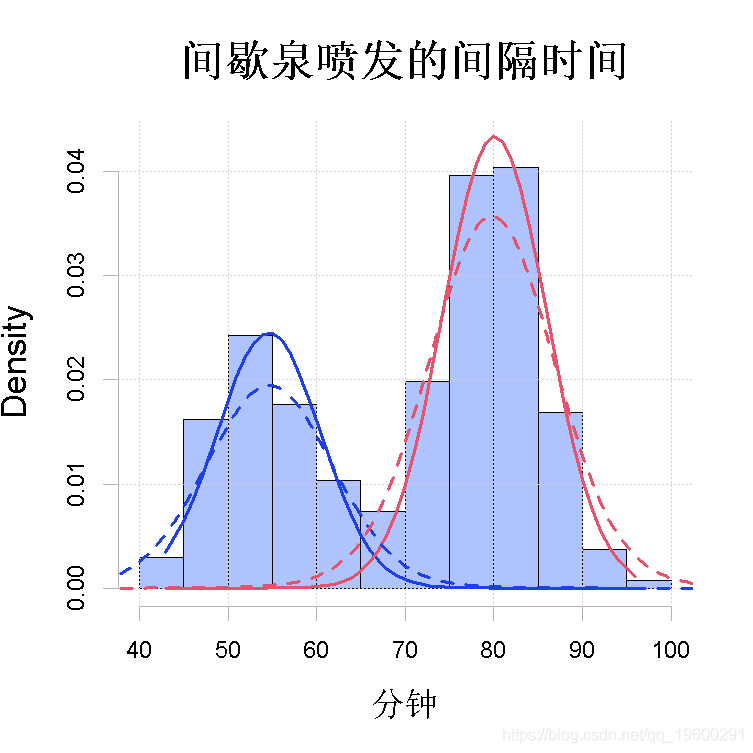
作为一个例子，我们考虑对图1中描述的间歇泉喷发间隔时间等待数据进行单变量正态混合分析。这种完全参数化的情况对应于第1节中描述的单变量高斯家族的混合分布，其中（1）中的第j个分量密度φj（x）为正态，均值为μj ，方差为σ 2 j 。
对于参数(μj , σ2 j )的M步， j = 1, . . 这个EM算法对这种单变量混合分布的M步骤是很简单的，例如可以在McLachlan和Peel（2000）中找到。
mixEM(waiting, lambda = .5)

文章图片

上面的代码将拟合一个二成分的混合分布（因为mu是一个长度为2的向量），其中标准偏差被假定为相等（因为sigma是一个标量而不是一个向量）。

文章图片

【变量|拓端tecdat|R语言有限混合模型(FMM)及其EM算法聚类分析间歇泉喷发时间】图1:对数似然值的序列， Lx(θ (t))

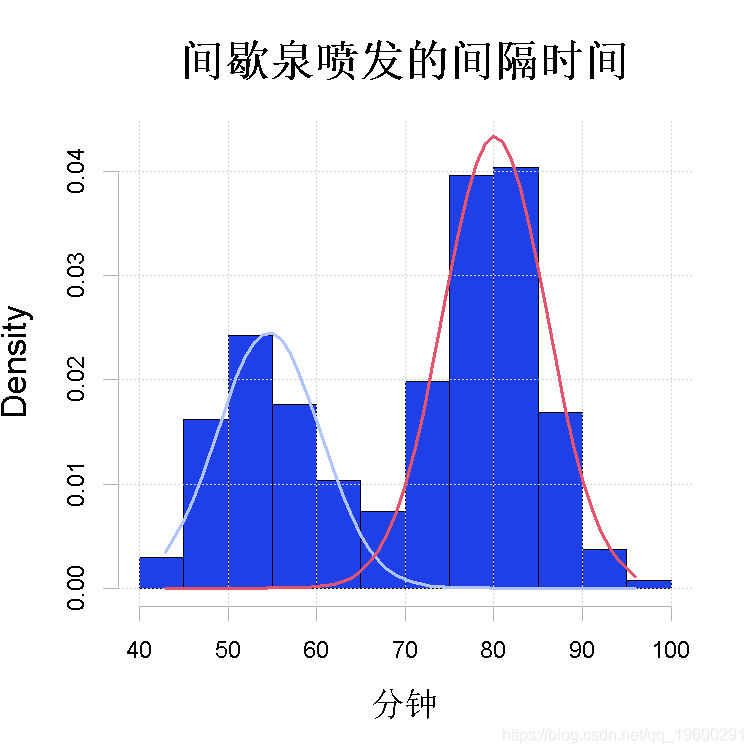
文章图片

图2：用参数化EM算法拟合间歇泉等待数据。拟合的高斯成分。

R> plot(wait1, density = TRUE, cex.axis = 1.4, cex.lab = 1.4, cex.main = 1.8,
+ main2 = "Time between Old Faithful eruptions", xlab2 = "Minutes")

两个图：观察到的对数似然值的序列t 7→Lx(θ (t))和数据的直方图，其中有N(?μj , σ? 2 j)的m(这里m=2)个拟合的高斯分量密度， j=1, . . .， m ，叠加在一起。估计θ?

变量|拓端tecdat|R语言有限混合模型(FMM)及其EM算法聚类分析间歇泉喷发时间

文章图片

另外，使用summary也可以得到同样的输出。
summary(wait1)

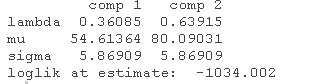
文章图片

3. Cutpoint methods切割点方法传统上，大多数关于有限混合模型的文献都假设方程（1）的密度函数φj（x）来自一个已知的参数族。然而，一些作者最近考虑了这样的问题：除了确保模型中参数的可识别性所需的一些条件外， φj（x）是不指定的。我们使用Elmore等人（2004）的切割点方法。
我们参考Elmore等人从-63开始，一直到63大约以10.5的间隔采用切点。然后从原始数据中创建一个多指标数据集，如下所示。

R> cutpts <- 10.5*(-6:6)
R> mult(data, cuts = cutpts)

一旦创建了多指标数据，我们可以应用EM算法估计多指标参数。最后，计算并绘制出方程的估计分布函数。图3给出了3分量和4分量解决方案的图表；这些图表与Elmore等人（2004）的图1和图2中的相应图表非常相似。

R> plot(data, posterior, lwd = 2,
+ main = "三分量解")

图3(a)

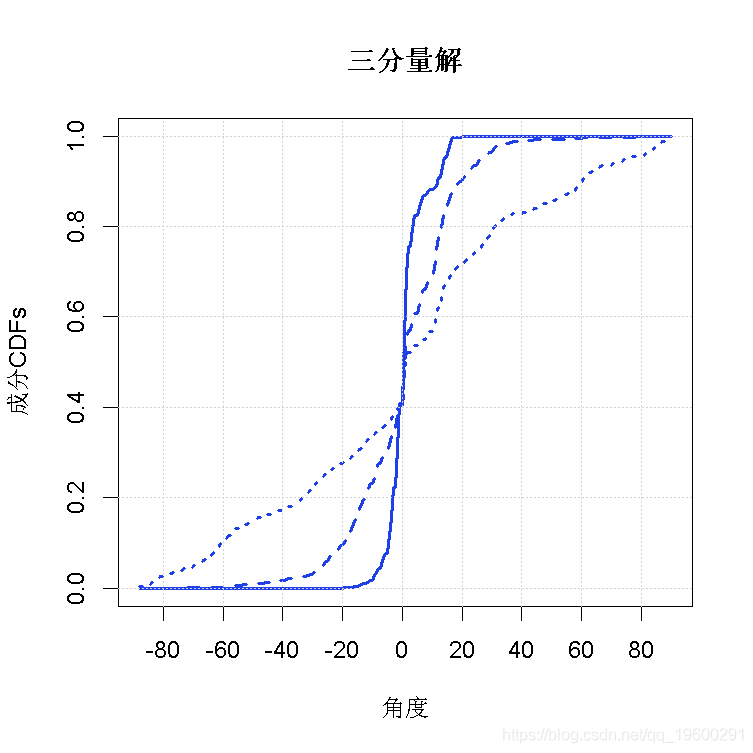
文章图片

图3(b)

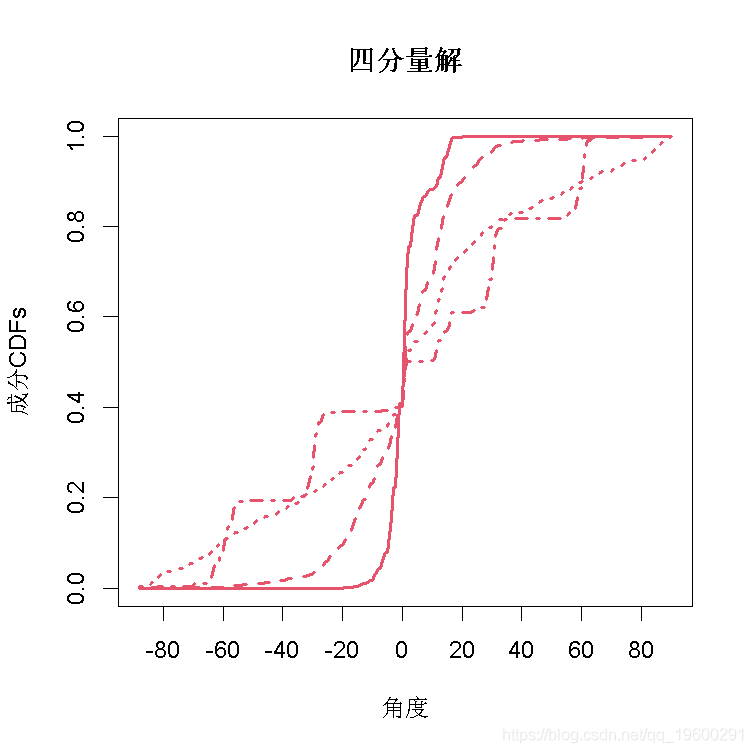
文章图片

同样可以用summary来总结EM输出。

文章图片

单变量对称、位置偏移的半参数例子在φ(-)相对于Lebesgue度量是绝对连续的额外假设下， Bordes等人(2007)提出了一种估计模型参数的随机算法，即(λ, μ, φ) 。一个特例

R> plot(wait1, which = 2 )
R> wait2 <-EM(waiting)
R> plot(wait2, lty = 2)

图4(a)

文章图片

文章图片

图4(b)
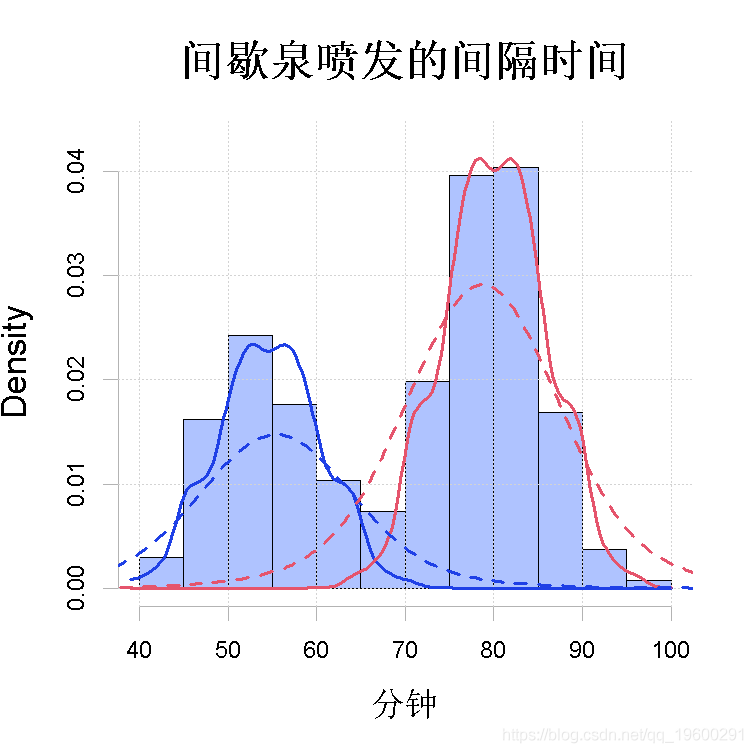
因为半参数版本依赖于核密度估计步骤（8），所以有必要为这个步骤选择一个带宽。默认情况下，使用"Silverman的经验法则"（Silverman 1986）应用于整个数据集。
R> bw.nrd0(wait)

文章图片

但带宽的选择会产生很大的不同，如图4(b)所示。

> wait2a <- EM(wait, bw = 1)
> plot(wait2a
> plot(wait2b

我们发现，在带宽接近2的情况下，半参数解看起来非常接近图2的正态混合分布解。进一步降低带宽会导致图4(b)中的实线所表现出的 "凹凸不平" 。另一方面，在带宽为8的情况下，半参数解效果很差，因为算法试图使每个成分看起来与整个混合分布相似。

文章图片

最受欢迎的见解
1.R语言k-Shape算法股票价格时间序列聚类
2.R语言中不同类型的聚类方法比较
3.R语言对用电负荷时间序列数据进行K-medoids聚类建模和GAM回归
4.r语言鸢尾花iris数据集的层次聚类
5.Python Monte Carlo K-Means聚类实战
6.用R进行网站评论文本挖掘聚类
7.用于NLP的Python：使用Keras的多标签文本LSTM神经网络
8.R语言对MNIST数据集分析探索手写数字分类数据
9.R语言基于Keras的小数据集深度学习图像分类