一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质( 二 )

2025-12-27

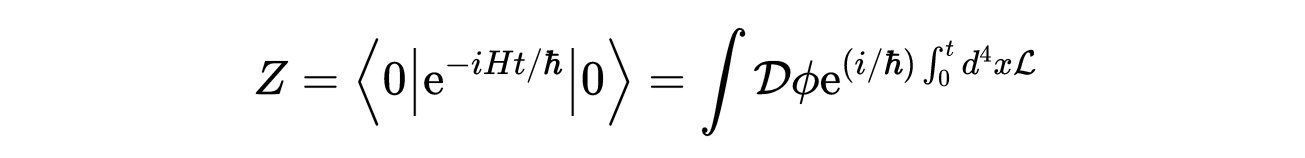
文章插图

式8：生成泛函或配分函数，量子场论中的一个关键对象。

真空状态如上面的图4所示。
关于量化方案在本文中，我将采用量化的路径积分法（而不是标准积分法）。正如我们刚才看到的，该方法基于相对不变的拉格朗日量，使得路径积分也具有明显的不变性。此外，积分内的对象是经典量。
我们注意到，与正则量子化相比，该方法涉及到视角的转变。系统的哈密顿动力学由式6定义。因此拉格朗日量成为量子场论“最基本的规范”。
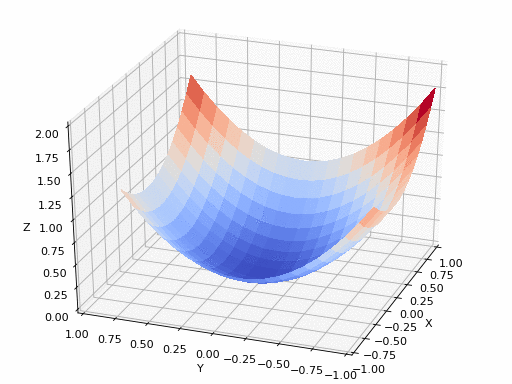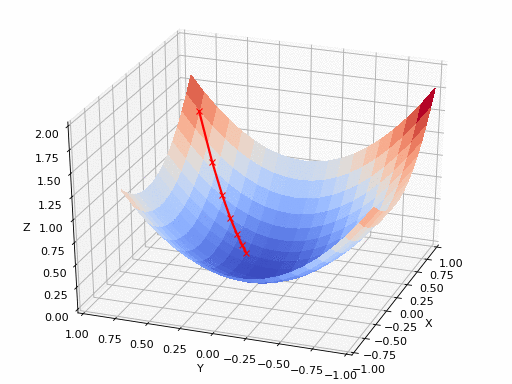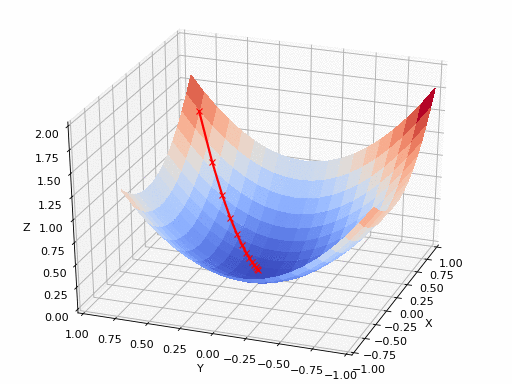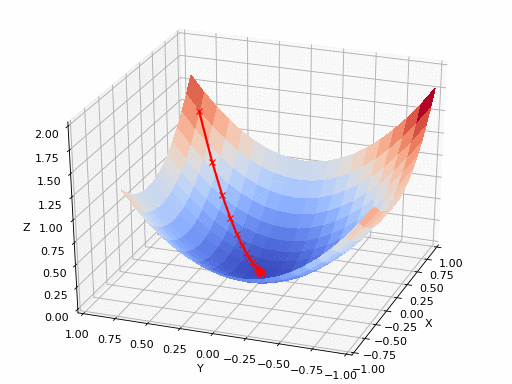
让我们回到实标量场论的式4。欧拉-拉格朗日运动方程应用最速（陡）下降法近似于作用：

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式9：求作用的极值。

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

图6：显示最陡下降方法的动画。

其结果就是普遍存在的克莱恩-戈登方程：

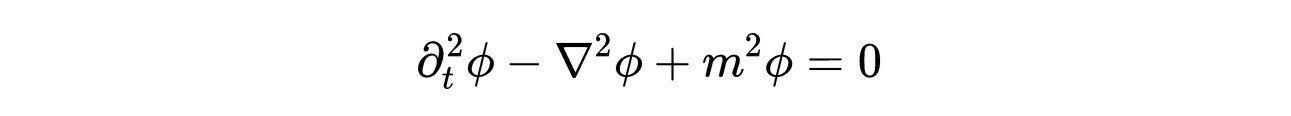
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式10：质量标量场服从的克莱恩-戈登方程。

跃迁振幅的显式计算重写拉格朗日方程，我们得到：

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式11：式8中的生成泛函或配分函数，明确地写出拉格朗日密度。

其中包括外部电势或源电流J。包含J的项是与标量场φ (x)和源电流J(x)之间的相互作用有关的势能项。
这个积分只是高斯积分的一个复杂版本：

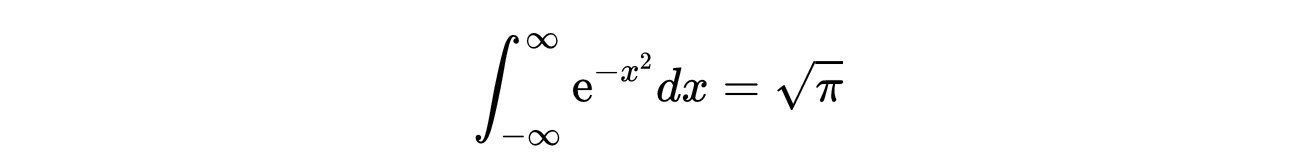
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图
可以用高斯积分的标准程序来计算。我们得到：

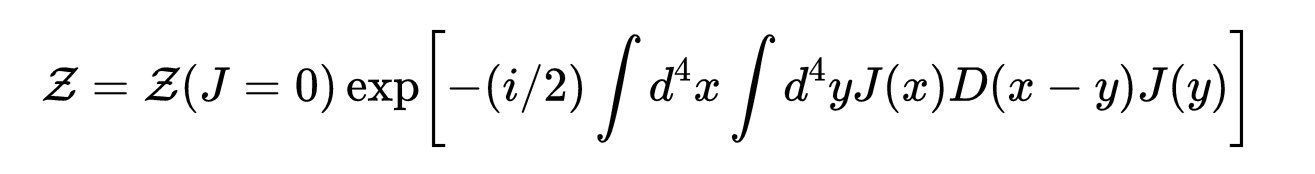
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式12：对?进行积分后的生成函数表达式。

函数D(x)是自由传播子，它是以下微分方程的解：

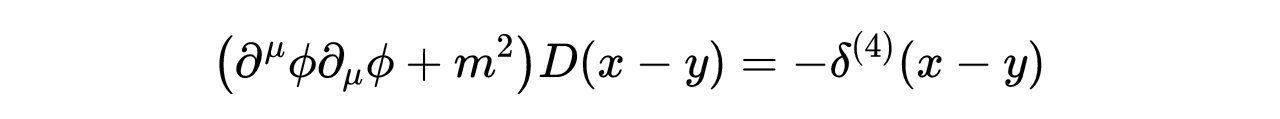
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式13：自由传播子所服从的方程。

由式13，我们可以计算动量为p的粒子在动量空间中的费曼传播子，它是被积函数中D(x-y)的指数相乘的对象：

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式14：自由传播子写成动量空间传播子的傅里叶变换。

其中ε是一个很小的正量。给定时空的信号是度规张量对角化后的矩阵表示法上的正负数。对于一个n维洛伦兹流形：

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式15：n维洛伦兹流形。

信号是(-，+，+，+，…，+)，其中有一个0和n-1个1（在我们的讨论中，n=4）。
如果我们用欧几里德符号(+，+，…，+)来代替，在质量项变为正数之前，会失去ε。传播函数为：

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式16：自由传播子的欧氏版本，作为欧氏动量空间传播子的傅里叶变换。

现在让我们进入我们讨论的第二个要素，那就是一维时空中的量子引力。
一维量子引力我们现在的目标是建立一个一维的量子场论，在那里场与引力相互作用。要构建一维量子场论，我们需要两个基本要素：

理论“存在”的时空（我们的宇宙）
我们要研究的对象，也就是这里的场。它们可以是几种类型，但这里我只考虑标量场。

一维紧流形
在一维上，只有两个可能的紧流形（封闭和有界流形），即：

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

图7：一维中仅有的两个可能的紧流形。

我们可以用实数标记这两个流形的点，区间I和圆S1可以被t∈[0,t]参数化。区别在于，在S1中，我们确定了t和t +T。在一维上，每个流形都有相关的度规g——1 x1张量。我们用以下方法分别表示度规和逆度规：

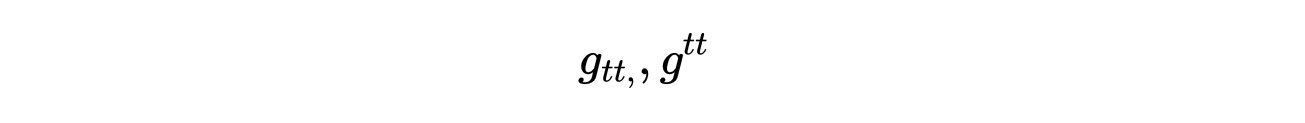
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

式17：一维流形的1x1度规（下标）和1x1逆度规（上标）。

一个数学插曲本节将简要介绍回调（pullback）的概念，以备后用。
回调
微分几何中一个有用的概念是回调。考虑下面图中所示的两个流形M和N、映射?、f及其组成。

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

文章插图

图8：回调

从图中可以看出：

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

推荐阅读

上一篇：黑洞和中子星，两个“大佬”的激情碰撞，可能揭开宇宙膨胀的秘密

下一篇：太阳系之大就很难想象最近的星际旅行也要150000年