易坊好文馆

  1. 首页 > 生活百科 >

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质

一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
量子引力可以说是理论物理学的圣杯。在这篇文章中，我将展示一维的量子引力理论，它描述了四维时空中的粒子。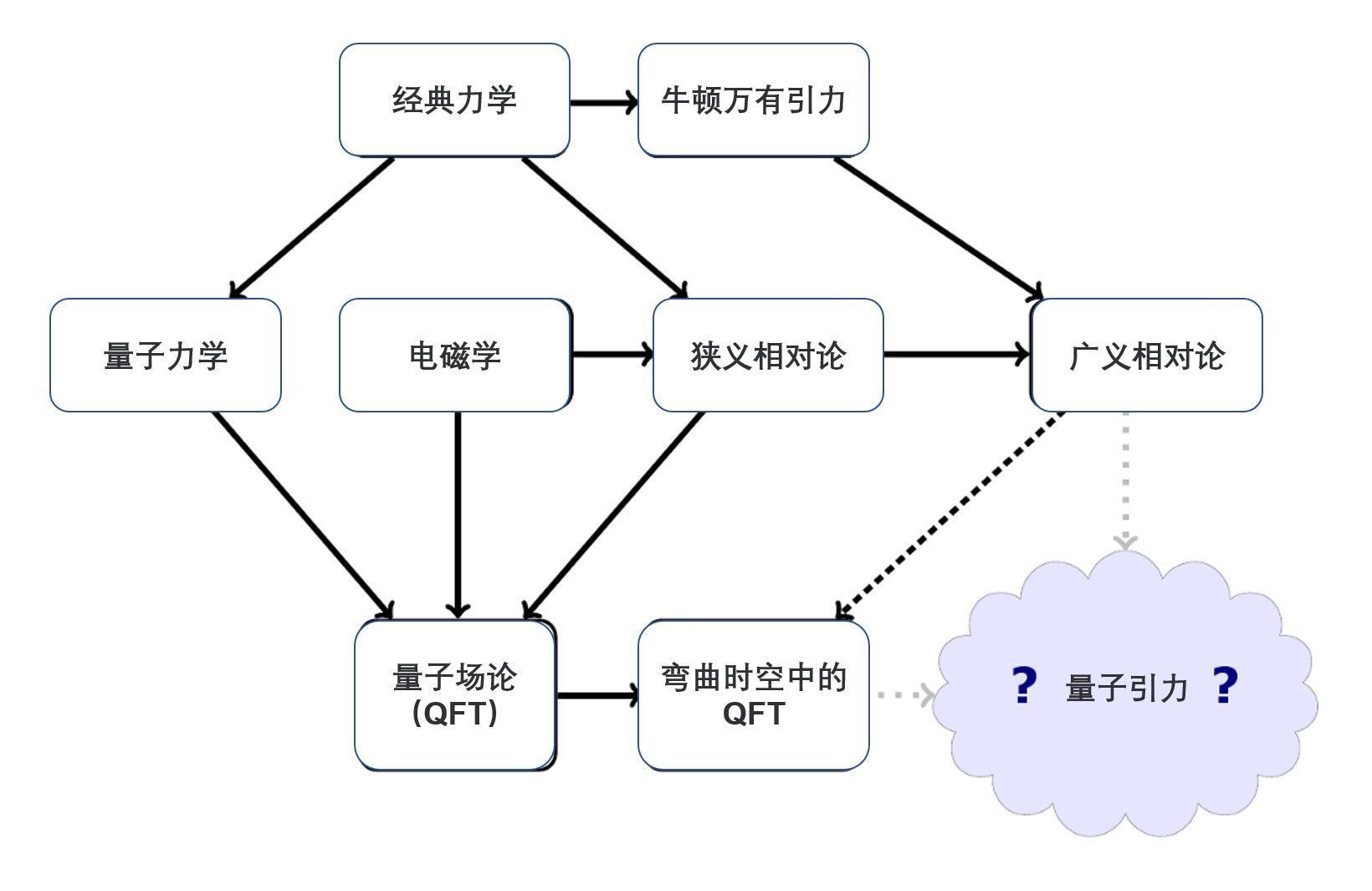
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图

  • 图1：这张图显示了量子引力在物理理论中的位置。
其中一个要素就是费曼的路径积分公式。它将跃迁振幅表示为系统从某个初始状态到某个最终状态的所有可能时空路径的加权和。在量子引力的背景下，路径积分的平均值不是在时空中的路径上，而是在时空的几何上（然而，正如 威腾所指出的，这种描述在微观层面上可能是无效的）。
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
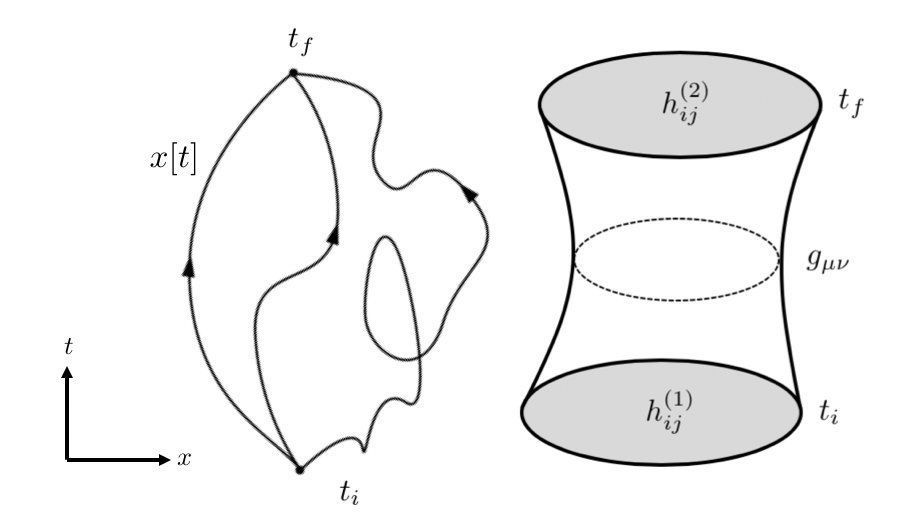
  • 图2：左边显示了对量子力学求和。右边是量子引力中相应的和，其中时空g类似于路径x[t]。时空g连接两个三维空间h。
要在四维时空中建立一维量子引力和量子场论（QFT）的对应关系，我们首先需要了解这两个成分中的每一项。让我们从量子场论开始。这里所遵循的方法论通常被称为QFT的世界线视角。
标量场理论与克莱恩-戈登方程量子场是经典场的延伸，如电磁场和爱因斯坦的引力场，到量子框架。
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 图3：这幅图显示了地球磁场与太阳太阳风的关系。
《量子场理论概论》的作者Zee对量子场论的定义如下：
量子场论是对生命短暂本性的回应。
这个定义来自以下观察：结合狭义相对论和量子力学意味着粒子“可以生也可以死”。
让我们来理解其中的原因。能量-时间不确定性原理指出，人们不能确定只存在于短暂时间内的量子态的能量。这在数学上可以表示为：
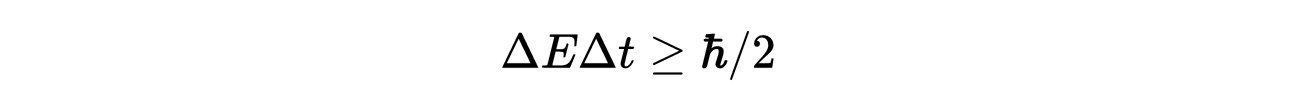
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 式1：时间-能量不确定性关系。
事实上，真空能量波动剧烈。如下图所示，允许（粒子-反粒子）虚粒子对的产生。
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
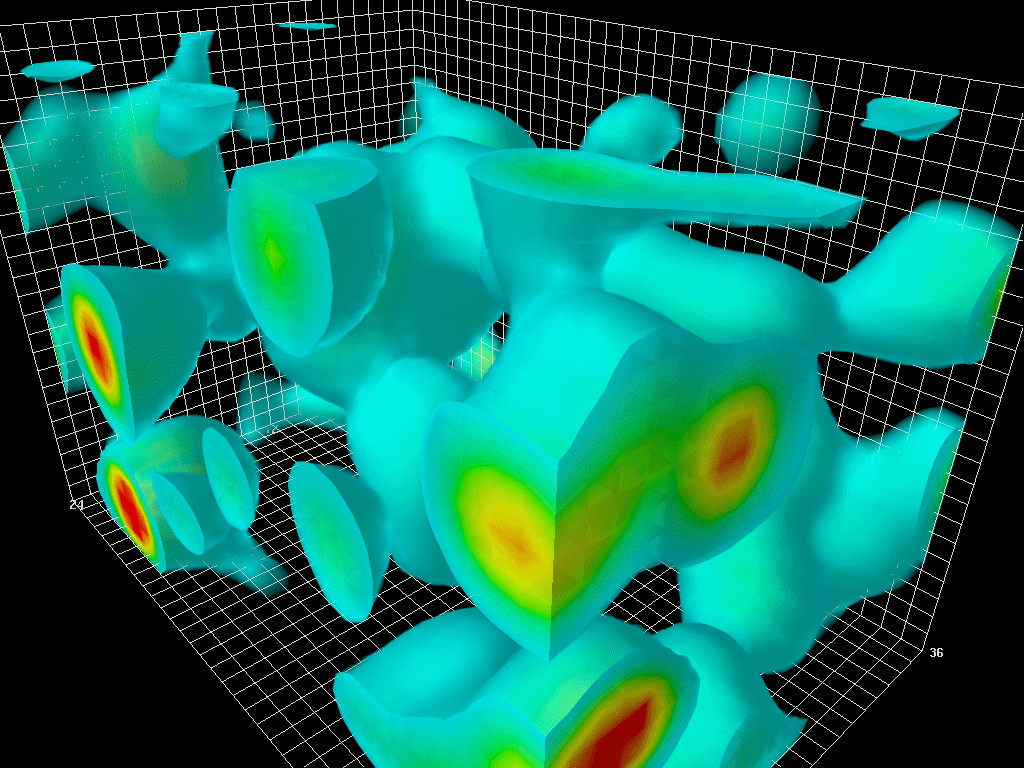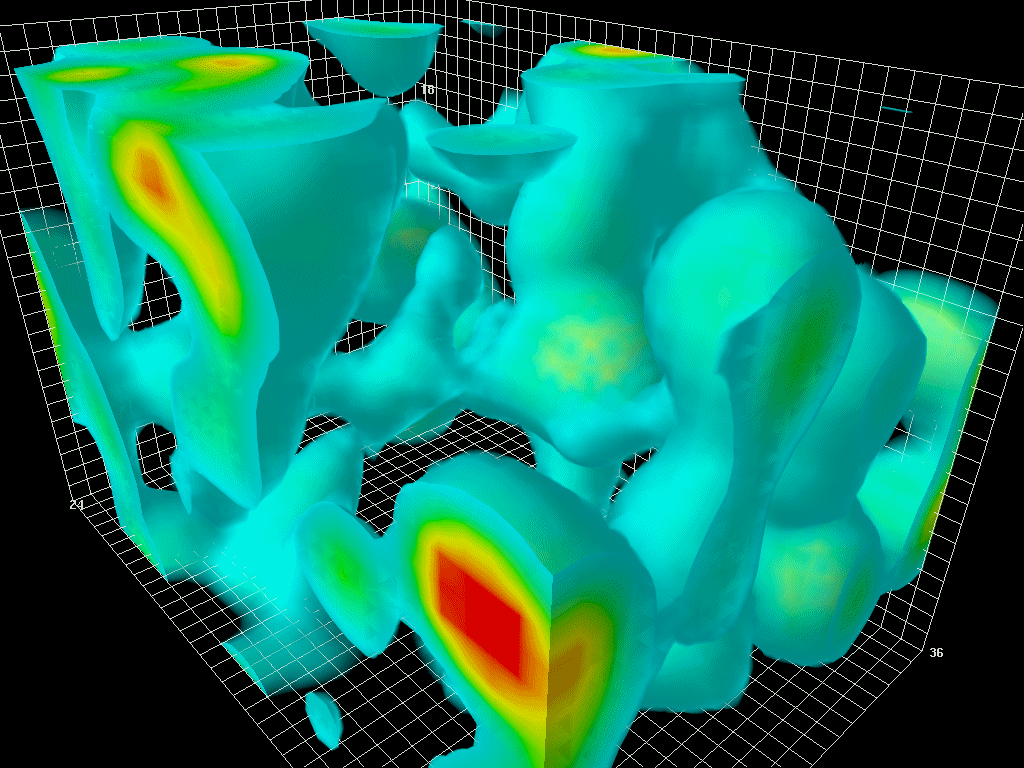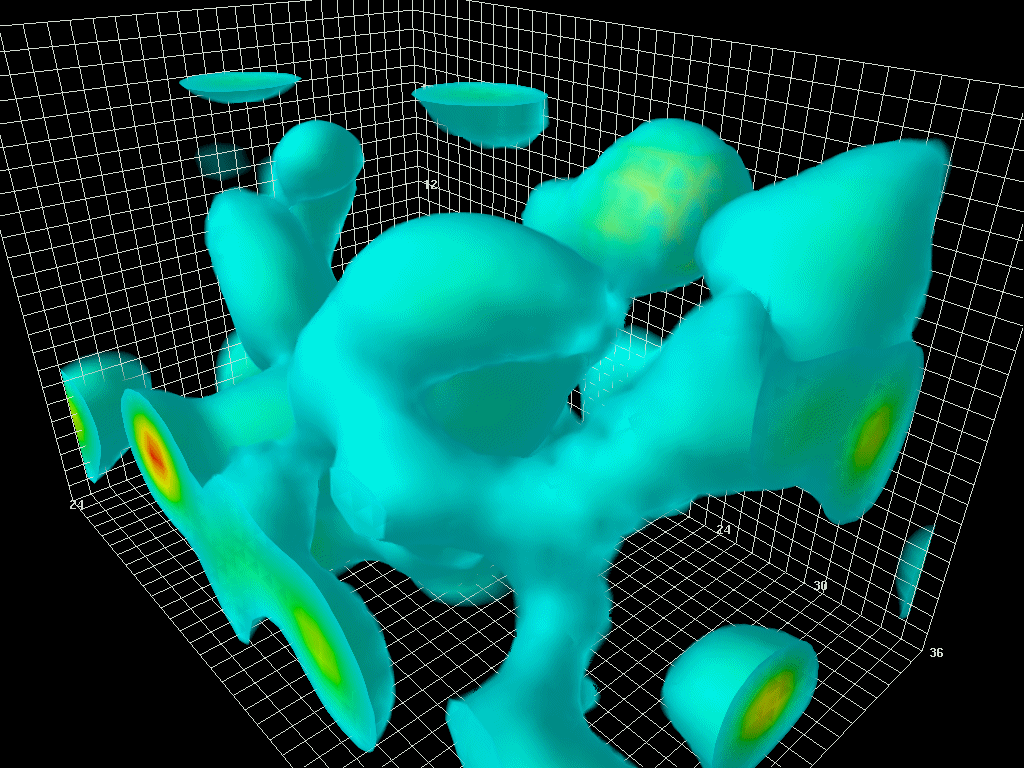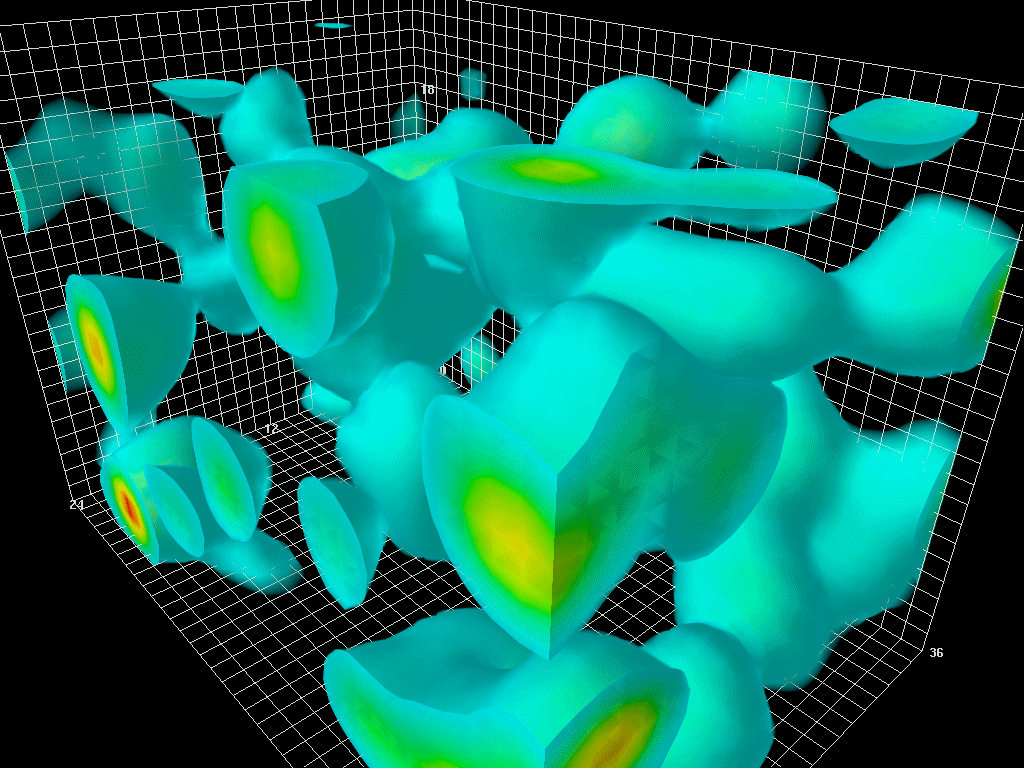
  • 图4：真空波动，根据能量-时间不确定性原理，是一个空间区域内能量量的短而强烈的变化。
作为狭义相对论的结果，这可能导致能量转化为质量——新粒子可以“诞生”，现有粒子可以“消失”。问题是标准的量子力学框架不能解释这种现象，因此，需要修改。量子力学的改进版本是量子场论（QFT）。
此外，QFT使我们能够解释，为什么宇宙中有基本粒子的不可区分的“副本”——粒子仅仅是量子场的激发。
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 图5：这幅图显示了一个模拟粒子碰撞产生希格斯玻色子的过程。
简单的经典弦理论量子场相当抽象。为了给读者一些直观的感觉，我将使用N个质量m相互耦合的谐振子作为类比。只考虑垂直q_i(t)位移。
对应的作用是：
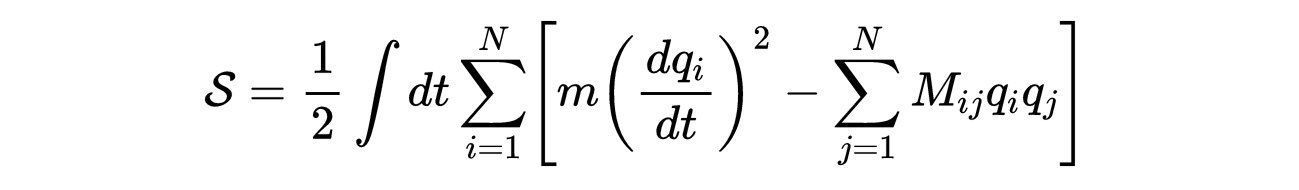
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 式2：N个谐振子的经典作用，其中M是一个对称的正定矩阵。
其中矩阵M是对称且正定的：
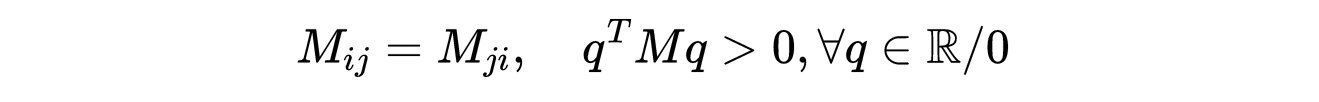
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 式3
对M进行对角化，我们得到了法向模态的作用：
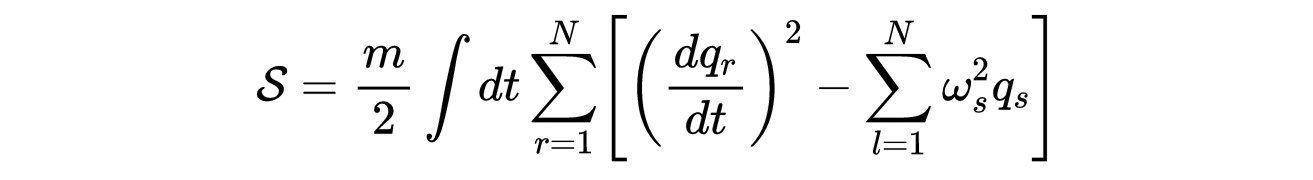
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 式4：法向模态的作用。
下一步是获取连续标量经典场?(x,t)的作用。标量场是QFT中最简单的场类型。将其中的φ (x,t)解释为每个点x上的无限个振荡器集是一种有用的方法。注意，当我们取连续极限时，振子的索引i变成了空间坐标x。连续极限中的作用变成：
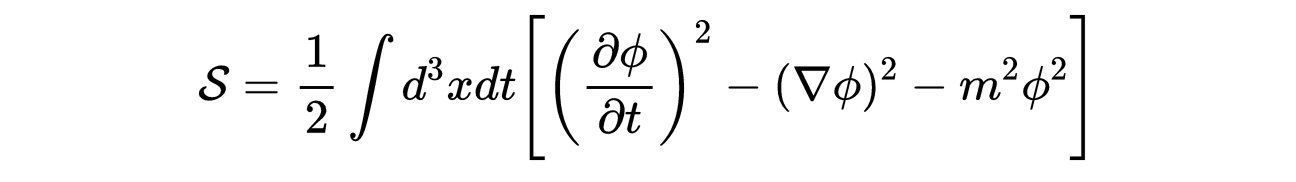
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 式5：自由质量标量场的作用。
根据量子力学的路径积分公式，系统在I和F两态之间发生跃迁的概率为：
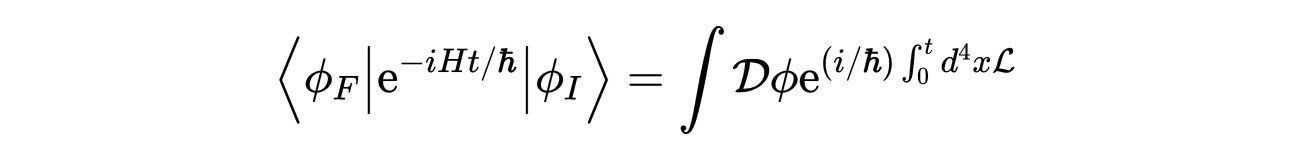
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 式6：量子力学路径积分公式中的跃迁振幅。
式中拉格朗日密度为：
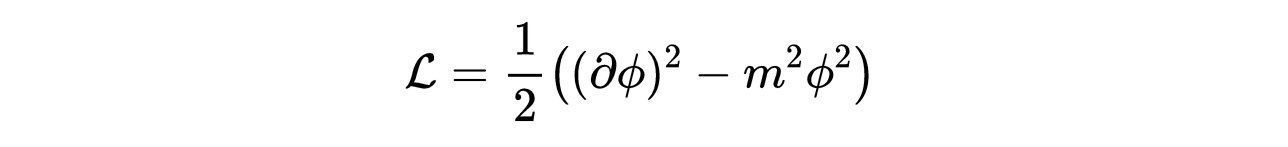
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
  • 式7：质量标量场的拉格朗日密度。
这里：
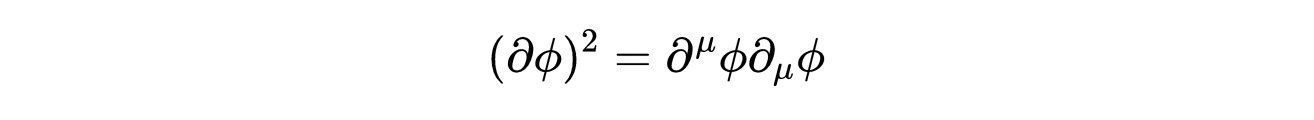
一维量子引力—解释4维时空中的自由粒子，揭示生命短暂的本质
文章插图
生成泛函或配分函数是式6的一种具体情况，是量子场论中的一个关键对象，它是从真空状态转回自身的跃迁振幅，其表达式为：

推荐阅读


上一篇：黑洞和中子星，两个“大佬”的激情碰撞，可能揭开宇宙膨胀的秘密

下一篇：太阳系之大就很难想象 最近的星际旅行也要150000年