
本文图片
本文图片
Jon Fox for Quanta Magazine
以下为朗读小姐姐全文音频
作者 | Stephen Ornes
翻译 | 茹小茹
审校 | 酷炫脑主创小注
美工 | 雪今金
朗读 | 胡恩
编辑 | 湘蓉
为了解决更加多元复杂的问题 , 科研人员开创了一个人工智能系统 , 这远比诸多繁琐的数学公式更加有用 。
七十多年前 , 人工智能领域的一群顶尖科学家引入了神经网络的概念 , 这是大脑工作原理探索中的革命性进步 。 人脑的数十亿个神经元连接成神经网络 , 对感觉信息进行处理 , 并介导经验性学习过程 。 人造神经网络也可以通过层层结构对大量数据进行筛选处理 , 学习运算规则 , 进而建立可行的识别预测模式 。
到目前为止 , 神经网络被看作是人工智能的万灵丹 。 它具有各种模式识别技术挑战的完成潜力 , 能够完成极其自然的语言翻译并对手机相册中重复出现的面孔进行识别和分类等 。 由神经网络驱动的电脑程序甚至已经在围棋和国际象棋比赛中击败了世界冠军 。
然而 , 神经网络往往不擅于解决繁复的代数问题 , 比如微积分或常微分方程 , 其主要原因在于数学学科本身的精确性质 。 神经网络仅仅擅长概率运算和模式识别 , 比如怎样翻译西班牙语最通顺 , 或者某张特定面孔长什么样子 。
去年年末 , 这种情况发生了变化 , 巴黎人工智能研究小组的两位计算机科学家纪尧姆·兰普尔和弗朗索瓦·沙顿 , 首次提出了用神经网络模式解决代数问题的途径 。 这种方法并不涉及数值得运算和估计 。 相反 , 他们利用了神经网络的优势 , 将数学问题转化为了我们已经解决的熟悉问题: 自然语言翻译 。
本文图片
本文图片
弗朗索瓦·沙顿(左)和吉劳姆·兰普尔 , Facebook在巴黎的人工智能研究小组的计算机科学家 , 想出了一种方法 , 把符号数学翻译成神经网络可以理解的形式
研究人工智能在数学应用的沙顿说:“我们都主修数学和统计学 , 所以数字是我们的基本语言 。 ”
兰普尔和沙顿设计的程序可以求解复杂的积分和微分方程 , 这要一定程度上归因于数学软件包中明确的内置运算规则 。
该新程序利用了神经网络的一个明显优势:深度学习 。 因此 , 斯坦福大学的心理学家杰伊 · 麦克利兰称“规则内外无区别 。 ”他正在尝试利用神经网络模拟人类的数学学习模式 。 实际上 , 运算程序从未在复杂的积分运算上出错 。 理论上讲 , 这种计算机可以自行推导出一些非同寻常的“规则” , 并帮助一些棘手的问题攻克难关 , 比如新定理的发现或理解神经网络的自身性质 。
当然 , 以上仍处于假想阶段 。 但很明显 , 这个团队已经回答了几十年前的古老问题——人工智能完成代数运算吗?答案无疑是肯定的 。 “他们的研究模式已经十分成熟了 。 算法已经建立 , 精妙绝伦的假设也已经产生 。 ”人工智能研究组织Open AI的联合创始人沃伊切赫·扎伦巴说 。
“他们成功塑造了神经网络概念 , 使得一般规则之外的问题得以解决 , 这太令人兴奋了 。 ”麦克莱兰说 。
计算机数学语言学习
计算机最擅长于处理数字 。 代数运算系统将上百种算法与预设指令编码融合在一起 , 严格遵循规则 , 执行特定操作 , 且无法兼容异常情况 。 它们针对一些学术问题提出的众多方案足以解决相关的工程和物理应用难题 。
本文图片
图源网络
神经网络则与此不同 , 通过大数据(规模越大越好)和统计学规律估算出逼近真实的近似值 , 这意味着其运行基础并非固定规则 。 在这个过程中 , 程序不断自我优化 , 从而获取众多选项中的最优解 。 自然语言翻译就是一个典例:程序并不会逐字翻译 , 而是联系上下文语境对短语进行匹配 。 Facebook的研究人员认为这进一步增强了问题解决的自由性 , 因而也是程序进行代数运算的优势 。
这种自由在一些前路未卜的领域尤其实用 , 比如集成 。 数学界流传着一句古老的谚语: “分解不过是机械行为 , 而整合是一种艺术 。 ”比如 , 我们通过一些直截了当的步骤就可以对某个函数进行求导 , 但积分求解往往需要一些其他的灵感 , 它们更贴近直觉而非机械计算 。
Facebook团队认为 , 这种“直觉”可以用模式识别进行近似 。 沙顿说:“集成是数学中与模式识别最相似的问题之一 。 ”因此 , 尽管不理解什么函数的概念和变量的意义 , 但神经网络的确发展出了一种知其然却不知其所以然的本能 。
为了使神经网络具有数学家一般的数学符号处理能力 , 沙顿和兰普将数学表达式转换为了一种更实用的形式——算法树(类似于图解句) 。 加、减、乘、除、乘方、三角函数等数学运算相当于树杈的分支点 , 参数(变量和数字)则相当于树叶 。 除了极少数例外 , 算法树能够成功对大部分长表达式进行嵌套运算 。
兰普说:“当看到一个复杂函数时 , 我们可以将其看作简单函数的复合体 , 并对解决方案有所直觉 , 我们认为 , 这个模型就是对符号中寻找解答线索的尝试 。 ”他说 , 这个过程与其实与人类计算积分(甚至是所有数学问题)的方式相似 , 即将其简化为我们曾解决过的可处理子问题 。
在提出该体系结构之后 , 研究人员使用一组基本函数生成了几个训练数据集 , 总计约2亿个算法树 。 他们将这些数据“输入”到神经网络中 , 进而令其自行探索问题的解决方案 。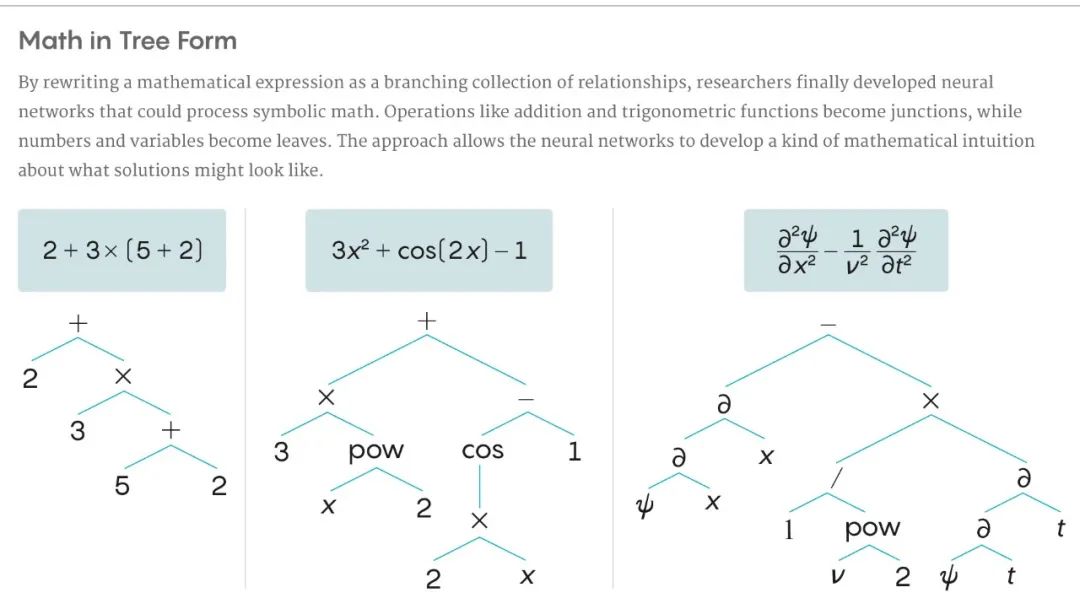
本文图片
5W信息图
训练结束后 , 就是验收成果之时 。 科学家将一个由5000个方程组成的测试集输入了计算机 , 虽然这一次没有标准答案 , 但神经网络仍以出色的成绩通过了测试: 它成功地为绝大多数问题找到了精确而全面的计算方法 , 尤擅于积分(几乎没有失误) , 但在常微分方程方面稍逊一筹 。
对于大部分题目 , 这个程序只用了不到1秒钟就找到了正确的解决方案 。 在集成问题上 , 它在速度和准确性方面优于 Mathematica 和 Matlab等软件包中的求解器 。 研究小组称 , 神经网络解决了这些生意人无从下手的问题 。
黑匣子深处
尽管结果如此 , 数学家罗杰·格蒙德森 , Mathematica的研发公司——Wolfram 的主管 , 仍对比提出了质疑 。 Facebook的研究人员将神经网络与 Mathematica 的几个函数进行了对比 , 除了积分和微分外 , Mathematica还可以搞定其余数百种运算工具 。
格蒙德森还指出 , 尽管训练数据集规模巨大 , 但这些方程只是含有单个变量的初级函数 。 他说: “这只是数学界的冰山一角” 。 对于物理学和金融学中经常使用的高级函数 , 比如误差函数或贝塞尔函数 , 神经网络并未对其进行测试 。 但Facebook 小组表示 , 只需要非常简单的修改 , 未来的神经网络就可以实现这些功能 。
加州大学圣巴巴拉分校的数学家弗雷德里克 · 吉布曾研究过用神经网络解决偏微分方程的方法 , 他不相信 Facebook 小组神经网络的绝对可靠的性 。 “我们需要确认 , 它可以在所有领域 , 而非某些特定选题上起作用 , 但显然事实并非如此 。 ”其他批评者则认为 , Facebook小组的神经网络并不能真正理解数学 , 它只是对数学题的结果进行了一种特殊形式的猜测 。
尽管如此 , 大多数人一致认为 , 新的方法总会被派上用场 。 格蒙德森和吉布相信 , 神经网络必将在下一代符号数学运算领域占有一席之地 。 “那将是一个浩瀚的领域 , 而神经网络只是众多工具中的一个 。 ”格蒙森说 。
除了解决具体的数学运算问题 , Facebook 小组的工作更是算法树原理和可行性的有力证明 。 剑桥大学数学家安德斯 · 汉森说: “如果某种技术能够让数学家解决从前无法下手的问题 , 那么他们一定会对此足够重视 。 ” 。
神经网络另一个可能的应用方向是自动定理生成器 。 数学家们开始越来越多地研究如何利用人工智能生成新的定理和证明 , 尽管“目前的技术水平还没有取得很大进展 , 但我们正在努力 。 ”兰普尔说 。
本文图片
图源网络
沙顿描述了该算法推动人工智能定理发现的两种途径 。 首先 , 它可以充当数学家的助手 , 通过识别已知定理中的固定模式帮助解决现有问题 。 其次 , 该机器可以自动生成一系列可能被证明成立的结果 , 而它们往往是数学家所忽略的 。 他说:“我们相信 , 既然集成已经实现 , 证明的成功应当也指日可待 。 ”
定理证明能力足以造出一个杀手级应用 , 这甚至超出 Facebook 团队自身的预计范围 。 推翻定理的常见方法是举出一个反例来证明它不成立 , 而有朝一日这种神经网络也可能会适合于这项任务 。
神经网络最令人不安的一点仍悬而未决: 没有人真正了解它是如何工作的 。 训练数据从一端输入 , 预测数据从另一端输出 , 但在这两者之间发生了什么 , 神经网络何以成为如此优秀的预言家 , 仍然是一个未解之谜 。
另一方面 , 数学好像也没那么神秘 。 查顿说:“只要将特定的数学问题作为测试 , 追踪计算机运算成功和失败的原因 , 我们就可以摸清神经网络的工作原理 。 ”
本文图片
本文图片
【数学|神经网络的数学天分】酷炫脑长期征集脑科学、心理学类文章 , 欢迎投稿
投稿请发邮箱:2829023503@qq.com
点这里 , 让朋友知道你热爱脑科学
推荐阅读
- 星链|石豪:在太空,马斯克和美国当局是如何作恶的
- 快报|“他,是能成就导师的学生”
- 区块|面向2030:影响数据存储产业的十大应用(下):新兴应用
- 年轻人|人生缺少的不是运气,而是少了这些高质量订阅号
- 生活|气笑了,这APP的年度报告是在嘲讽我吧
- bug|这款小工具让你的Win10用上“Win11亚克力半透明菜单”
- 苏宁|小门店里的暖心事,三位创业者的雪域坚守
- 历史|科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 空间|(科技)科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 生活|数字文旅的精彩生活






