哥德巴赫猜想|用跑得最慢的电脑程序，理解最高深的哥德巴赫猜想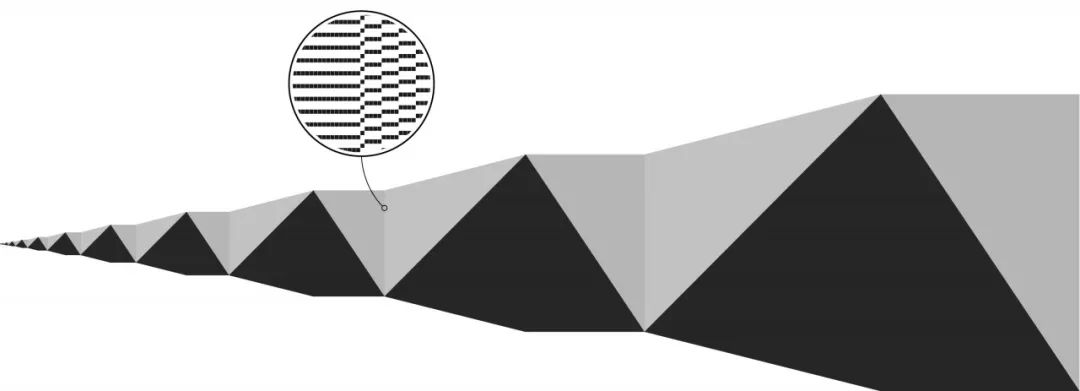_图灵机|停机问题|河狸家|停机

【哥德巴赫猜想|用跑得最慢的电脑程序，理解最高深的哥德巴赫猜想】

本文图片

五条规则的图灵机可视化。每列像素代表一步计算，步骤从左到右。黑色代表1 。最右边表示图灵机的停机。（图片来源：Peter Krumins/Quanta Magazine）
“忙碌的河狸”这个问题的目的是为了找到运行时间最长的电脑程序。对它的研究与哥德巴赫猜想、黎曼猜想等一系列数学难题建立了惊人而又深刻的联系。
撰文 | John Pavlus
翻译 | 张和持
编辑 | 吴非
程序员总想让代码跑的更快。可在1962年，匈牙利数学家蒂博尔·拉多（Tibor Radó）却提出了截然相反的问题：要怎么才能让一个简单的电脑程序在终止之前跑的尽可能久？拉多将这样跑得尽可能低效但仍有效的程序称为“忙碌的河狸” 。
自从《科学美国人》于1984年刊载这则问题之后，众多程序员和业余数学爱好者们纷纷开始寻找“忙碌的河狸” 。不过最近几年，由于与一些高大上的概念与数学未解的难题建立起联系， “忙碌的河狸”已经变成了非常严肃的数学问题，
得克萨斯大学的理论计算机科学家斯科特·亚伦森近日发表了一篇关于“忙碌河狸学”的调查，他说：“在数学上，娱乐和真正重要的问题，其边界非常模糊。 ”
最近一项研究表明，这些得跑到猴年马月的程序，或许能澄清一些数学命题，甚至告诉我们哪些内容是可知的。据研究者们称，忙碌的河狸能帮助我们判断一个数学问题的难易程度，比如哥德巴赫猜想和黎曼猜想。它能让人一目了然地看到数理逻辑到哪里就该走不下去了。逻辑学家库尔特·哥德尔（Kurt G?del）在大半个世纪之前就证明了，有一些命题既不能证明也不能证伪，也就是所谓的“不可知” 。不过现在，忙碌的河狸能为我们指出，这个“不可知”究竟位于什么地方，就如同一张古老的地图指引旅者走向世界的边缘。
无法计算的问题
“忙碌的河狸”这个问题，归根结底是关于图灵机——这是阿兰·图灵（Alan Turing）于1936年提出的一种理想化模型，其中有一条被分为正方形小块的长度无限的纸带，用笔在上面写或者擦去记号，这些操作需要满足一套给定的规则，比方说：
规则1. 如果正方形中含有0 ，则擦掉改成1；然后向右一格，使用规则2；
规则2. 如果正方形中含有1 ，那就不改，然后向左一格使用规则3；
……
每一项规则都像冒险棋一样。有些规则甚至可以让你跳回到之前的规则。在这些规则中，最终有一条“停机”的指令。图灵证明，如果时间充足，规则得当的话，图灵机就能做任何计算。
图灵称，为了真正计算出一个结果，图灵机最终必须得停机——不能卡死或者陷入循环。判别是否能停机的问题称为停机问题。他在1936年证明了世界上并不存在解决停机问题的万金油算法。
而“忙碌河狸”提出了以下问题：给定有限条规则，那么图灵机在停机之前最多能走多少步？

本文图片

蒂博尔·拉多（图片来源：俄亥俄州立大学档案）
比方说，我们只用一条规则，又要保证图灵机停机，那么这条规则肯定就必须包含停机指令。我们把停机问题的最长步数称为忙碌河狸数，那么BB(1) = 1 ，因为最多走一步就得停机。
自变量稍有增加，需要考虑的图灵机数量就会爆炸性增长。如果允许有两条规则，就有6561种图灵机，而它们中，只有一只“忙碌的河狸” ，它最长可以走6步。其他大多数图灵机都不停机，这些不停机的肯定不是“忙碌的河狸” ，不过对于一般的情况，要怎么才能区别出它们？毕竟前面图灵已经证明，不管图灵机跑了1000步还是100万步，都不能咬定图灵机不会停下来。
这样就使得寻找忙碌河狸的任务异常艰巨。规则的条数随便一改，我们就得从头开始找最长步数的图灵机，没有捷径。即是说，一般的“忙碌的河狸” 问题是“不可计算的“ 。
要证明 BB(2) = 6 和 BB(3) = 107 就已经非常复杂了，拉多的学生 Shen Lin 做出了这个成果，并于1965年获得了博士学位。拉多认为，BB(4) 的问题是“彻底的绝望“ ，不过还是有人在1983年解决了这个问题。除此之外，研究人员对于5条规则的情况，已经找到了一种图灵机，它在运行47 176 870步之后停机，也就是说， BB(5) 起码比这个数字要大。而 BB(6) 最小也得有7.4 × 1036534 。亚伦森说：“除非能找到新观点新思路，否则这个问题根本不可能得到解决。 ”
不可知的阈值
威廉·加斯塔克（William Gasarch）是马里兰大学学院市分校的计算机科学家，他关心的不是如何解决忙碌河狸数问题，相反他对“一般的不可计算问题”非常感兴趣。他和其他数学家正以此为基础，来估计数学上一些未解之谜的困难程度，或是看看这些问题究竟是否是可知的。
比方说哥德巴赫猜想，说的是对于任何大于2的偶数，总能分解为两个质数的和。要是这个问题能得到解决，那么数论这一学科将迎来史诗般的一刻，数学家对质数分布的了解也会更加深入。 2015年，一位网名为Code Golf Addict的Github用户发布了一台27条规则的图灵机代码。这台图灵机非常特别，它当且仅当哥德巴赫猜想不成立时，才会停机。其实很简单，它一开始工作，就会从4开始，挨着检查哥德巴赫猜想（当然也是靠遍历）。如果找到了所需的两个质数，就往上继续，以此往复。如果发现了不能表示为质数和的偶数，就会停机。
这种暴力的方法是不可能解决哥德巴赫猜想的，因为如果不停机，我们永远也不会知道猜想是不是正确的。不过， “忙碌河狸”问题为我们提供了一些思路。假如我们能计算出 BB(27)，那我们最多也只需运行 BB(27) 这么多步，再往上如果还没停机的话，就说明哥德巴赫猜想成立。毕竟 BB(27) 就是27规则停机问题的最大步数了。如果在此之前就停机，自然说明猜想不成立。
困难在于， BB(27) 是如此大的一个数，写下来都很难，要运行那么多次去检验哥德巴赫猜想，这在我们的宇宙中是远不可能的。虽然如此，那个巨大的数字仍然是一个具体的数，亚伦森称，这代表着我们对于数论领域“现有知识的陈述” 。
2016年，亚伦森同尤里·马季亚谢维奇（Yuri Matiyasevich）、斯特凡·奥里尔（Stefan O’Rear）一同做了一项类似的工作。他们设计了一台744条规则的图灵机，当且仅当黎曼猜想不成立时停机。黎曼猜想同样与质数的分布有关，是七大千禧问题之一，奖金高达一百万美元。亚伦森的这台图灵机只要运行 BB(744) 步，就能解决黎曼猜想。当然这里也是同样暴力的算法，挨着遍历直到反例出现。
BB(744) 比 BB(24) 又大了很多很多。不过亚伦森说道，要是深入研究一些简单的问题，比如 BB(5)， “就有可能从中发现一些本身就很有趣的数论问题。 ”例如，数学家帕斯卡尔·米歇尔（Pascal Michel）在1993年证明，目前保持着5规则步数记录的那个图灵机，其规则与考拉兹猜想中函数行为极其相似，而后者是数学中又一个著名的未解之谜。
亚伦森说道：“这么多问题可以归结为‘图灵机是否停机？’ ，那如果我们能知道所有的‘忙碌河狸数’ ，就能解决所有问题。 ”
最近，亚伦森又在使用一种基于“忙碌河狸”的方法去测量整个数学系统的“不可知阈值” 。哥德尔1931年证明了他那著名的不完备定理：对任意的公理集合，要么公理不相容（也就是会产生矛盾），要么不完备（存在不可证明的真命题）。而现代数学赖以生存的ZF集合公理也毫不例外地存在哥德尔界限。而亚伦森想要用“忙碌河狸”去估计它的边界具体在哪里。
2016年，他和他的研究生亚当·叶迪迪亚（Adam Yedidia）鼓捣出了一台7910条规则的图灵机，当且仅当ZF集合理论不相容时停机。这就是说 BB(7910) 次计算就能得到ZF集合理论的相容性。而这些公理本身在计算 BB(7910) 的时候是用不到的，就像我们算2 + 2 = 4的时候用不到集合公理时一样。
奥里尔紧接着提出了一个更简单的748条规则的图灵机，同样用来检测ZF公理。这样就把不可知的阈值降低了。奥尔良州立大学名誉教授，数理逻辑学家哈维·弗里德曼（Harvey Friedman）说：“这有些戏剧性，规则数变得没那么夸张了。 ”弗里德曼认为，这些数字还能进一步降低：“我觉得最终答案应该在50左右。 ”而亚伦森认为，真正的阈值应该接近BB(20)。
无论大小，不可知的阈值的确是存在的。亚伦森说道：“自从哥德尔以来，我们的世界就一直是如此（不可知）；而‘忙碌河狸’函数得以让这一切更加清晰明了。 ”
本文由微信公众号“环球科学”（ID：huanqiukexue）授权转载

编辑：观山不易

哥德巴赫猜想|用跑得最慢的电脑程序，理解最高深的哥德巴赫猜想

推荐阅读

2021年6月23日出生的男孩子五行属什么生辰八字取名

乔洋个人资料曝光这么有才华为何却要当主播做网红

什么的沙滩

五年级歇后语

女性更年期应该注意哪些？达到美容养颜很简单

2023江苏医惠保1号有等待期吗江苏医保什么时候截止

痛经喝红糖水真的管用吗？痛经喝红糖水能缓解吗？

芒果可以和牛奶一起榨汁吗

烟台二中有初中吗烟台二中是高中还是初中

龙利鱼为什么要去皮龙利鱼一定要去皮吗

驼背怎么改善呢

三丝鱿鱼球的做法（家常菜）

跨年夜最后一天祝福

白酒抽检酒精度不合格怎么处罚

蕨麻怎么煮才会烂呢

国家公祭日的宣传口号

红枣主要有哪些种类？红枣搭配哪些食物营养效果最好？

火腿小孩可以吃吗会性早熟吗

柑橘卷叶病解决方案

美瞳靠谱分享和选择