其中 ω = 2π/T 是角频率 , α_0/2 是直接分量 ,
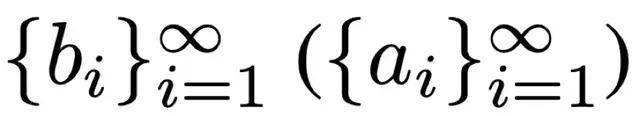
文章图片
是正弦(余弦)分量的系数 。 具体来说 , 当周期信号呈方波时 , 有:

文章图片
并推导出方波 s(t) 的 FS
【函数|NeurIPS 2021 | 华为诺亚Oral论文:基于频域的二值神经网络训练方法】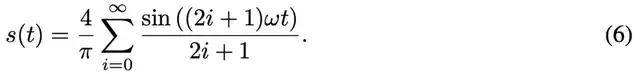
文章图片
注意到当信号被限制在单个周期内时 , 符号函数与方波等同:

文章图片
因此 , 符号函数也可以被分解为正弦(余弦)函数的组合 , 并且其导数如下:
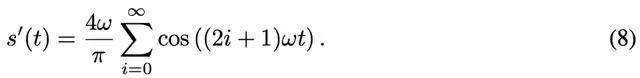
文章图片
然后 , 该研究提出使用上述等式 (8) 替换 STE 中的导数 , 以在反向传播期间更好地逼近符号函数 。
当将信号从空间域转换到频域 , 使用无限项时 , FS 分解是符号函数的无损表征 , 因此等式 (6) 可以重写为:
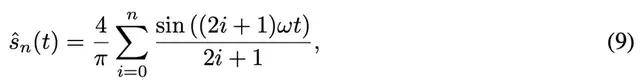
文章图片
其中 , n 是 FS 的项数 , 相应的导数是:
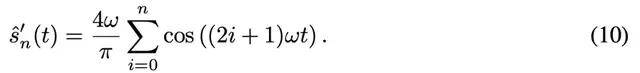
文章图片
然后该研究进一步证明了随着 n 的增加 , 估计值
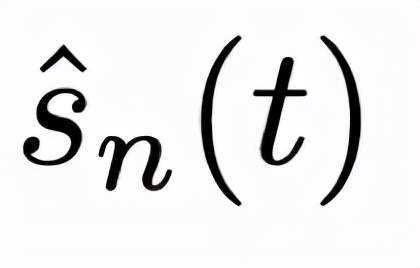
文章图片
和 s(t)之间的均方误差会逐渐减小 , 并在 n → ∞ 时收敛到 0 。
为了进一步补偿细微的逼近误差 , 该研究在训练阶段添加了一个噪声适应模块来细化梯度 。
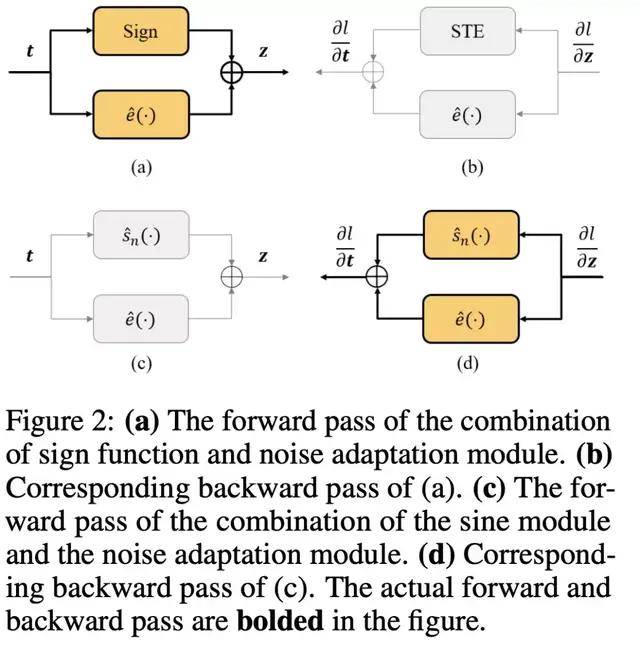
文章图片
实验及结果
为了展示 FDA-BNN 优越的性能 , 该研究在 CIFAR-10 数据集上进行了评估实验 , 实验结果如下表所示 。
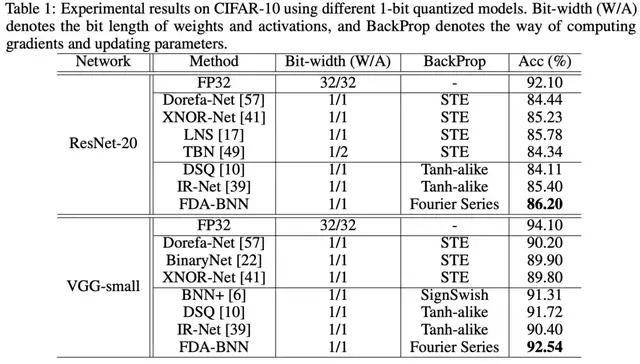
文章图片
消融实验
为了验证所提方法中每个组件的有效性、噪声适应模块和超参数的影响 , 该研究进行了一系列的消融实验 。
首先 , 该研究使用 ResNet-20 架构在 CIFAR-10 上实验验证正弦模块和噪声适应模块的效果 , 结果如下表所示 。

文章图片
推荐阅读
- Google|谷歌暂缓2021年12月更新推送 调查Pixel 6遇到的掉线断连问题
- 精度|将建模速率提升10倍,消费级3D扫描仪Magic Swift在2021高交会大显“身手”
- 四平|智慧城市“奥斯卡”揭晓!祝贺柯桥客户荣获2021世界智慧城市治理大奖
- 系列|2021中国航天发射圆满收官!年发射55次居世界第一
- 项目|常德市二中2021青少年科技创新大赛再获佳绩
- 选型|数据架构选型必读:2021上半年数据库产品技术解析
- 殊荣|蝉联殊荣!数梦工场荣获DAMA2021数据治理三项大奖
- 公司|外媒:2021,人类太空事业的重大年份
- 语境|B站2021个人年度报告发布:你共计看了多少个视频
- 最新消息|IT系统出错 英国银行给7.5万人多发11亿工资







