机器之心发布
机器之心编辑部
常规符号函数的梯度几乎处处为零 , 不能用于反向传播 。 为此 , 来自华为诺亚方舟实验室等机构的研究者提出一种在频域中估计原始符号函数梯度的新方法 。二值神经网络(BNN)将原始全精度权重和激活用符号函数表征成 1-bit 。 但是由于常规符号函数的梯度几乎处处为零 , 不能用于反向传播 , 因此一些研究已经提出尝试使用近似梯度来减轻优化难度 。 然而 , 这些近似破坏了实际梯度的主要方向 。
基于此 , 在一篇 NeurIPS 2021 论文中 , 来自华为诺亚方舟实验室等机构的研究者提出使用傅里叶级数的组合来估计频域中符号函数的梯度以训练 BNN , 即频域逼近 (FDA) 。 所提方法不影响占整体能量大部分的原始符号函数的低频信息 , 并且将高频系数使用噪声拟合模块 (noise adaptation module) 进行估计以避免大量的计算开销 。

文章图片
论文地址:https://arxiv.org/pdf/2103.00841.pdf
在几个基准数据集和神经架构上的实验表明 , 使用该方法学习的二值网络实现了 SOTA 准确率 。
数日前 , 在机器之心 2021 NeurIPS MeetUp China 上 , 论文一作许奕星为参会者解读了该论文 。
方法
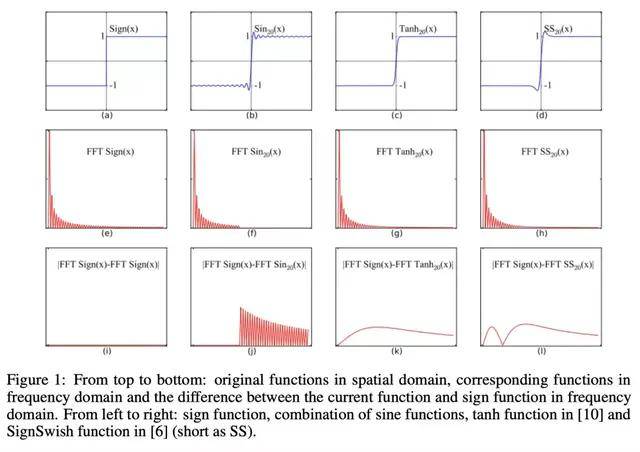
该研究提出的 FDA 方法 , 通过利用傅里叶级数 (FS) 来估计频域中的原始符号函数 , FS 估计是使用无穷项时符号函数的无损表征 。 在实际应用中 , 能量相对较低的高频系数会被忽略 , 以避免巨大的计算开销 , 并将符号函数表征为固定数量的不同周期正弦函数的组合 。 与现有的逼近方法相比 , 该研究所提出的频域逼近方法不影响原始符号函数的低频域信息 , 即占用符号函数能量最多的部分 。 因此 , 原始符号函数相应梯度的主要方向能够被更准确地保持 。
文章图片
在论文中 , 该研究对所提方法做了详细的理论表述 。
论文中用 f(·)和 f’(·)来表示原始函数及其对应的梯度函数 。 由于符号函数的梯度是一个无法反向传播的脉冲函数 , 需要应用进化算法(evolutionary algorithm)等零阶算法来达到最优解 , 但这是非常低效的 。 因此该研究提出找到一个代理函数 , 通过一阶优化算法(如 SGD)依靠实验求解 , 而理论上具有与符号函数相同的最优解 。
已有研究证明 , 任何周期为 T 的周期信号都可以分解为傅里叶级数的组合:
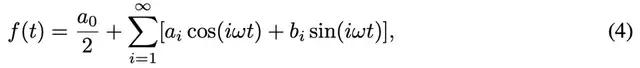
文章图片
推荐阅读
- Google|谷歌暂缓2021年12月更新推送 调查Pixel 6遇到的掉线断连问题
- 精度|将建模速率提升10倍,消费级3D扫描仪Magic Swift在2021高交会大显“身手”
- 四平|智慧城市“奥斯卡”揭晓!祝贺柯桥客户荣获2021世界智慧城市治理大奖
- 系列|2021中国航天发射圆满收官!年发射55次居世界第一
- 项目|常德市二中2021青少年科技创新大赛再获佳绩
- 选型|数据架构选型必读:2021上半年数据库产品技术解析
- 殊荣|蝉联殊荣!数梦工场荣获DAMA2021数据治理三项大奖
- 公司|外媒:2021,人类太空事业的重大年份
- 语境|B站2021个人年度报告发布:你共计看了多少个视频
- 最新消息|IT系统出错 英国银行给7.5万人多发11亿工资







