团队|高维等角线并非无限：MIT华人团队用谱图理论解决持续70年的难题_等角线|数学|理论|研究|高维

机器之心报道
编辑：杜伟、陈萍

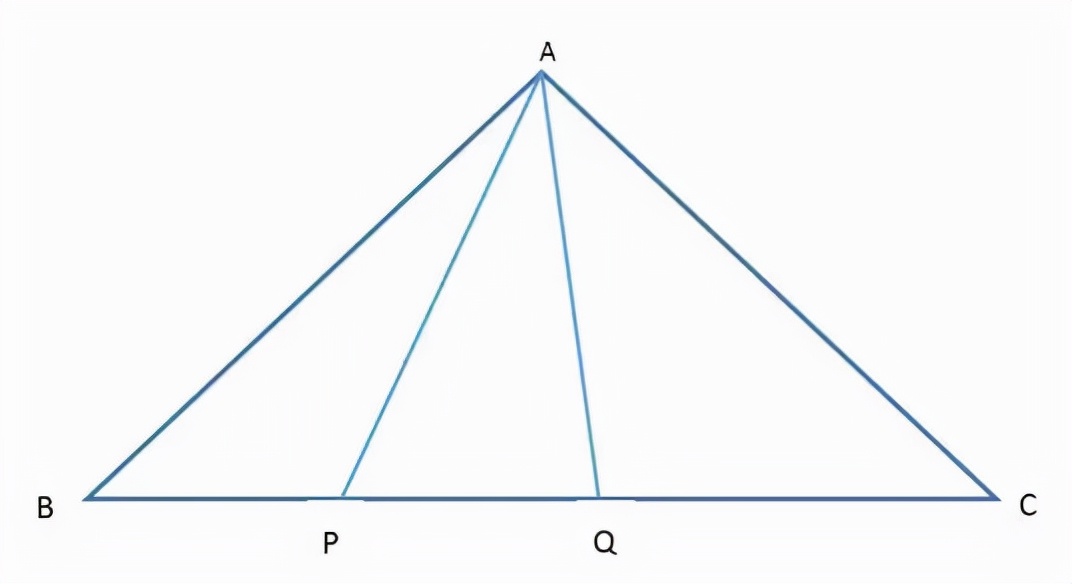
本想着或许可以取得一些不错的进展，没想到取得了意料之外的收获。

等角线（Equiangular Lane）是一个数学用语，通常在数学上这样表示：在△ABC 中，在线段 BC 上取 P、Q ，使得∠BAP=∠CAQ ，则称 AP、AQ 为△ABC 中的等角线。

文章图片

更简单的说，等角线是空间中通过一个点的线，其对角都是相等的。想象一下二维正六边形的三条对角线，三维正二十面体的六个对顶点的连接线，参见下图：

文章图片

然而，数学家们并不局限于三维。有研究者认为在更高维度也存在等角线，并且在高维度上，等角线的可能性几乎是无限的。据了解，这是一个困惑了数学家们至少 70 年的问题。
来自 MIT 的研究者认为在高维空间中等角线并不是无限的。他们突破性的研究决定了可以放置的线的最大可能数量，以便这些线以相同的给定角度成对分开。论文将发表在 2022 年 1 月的《数学年鉴》上。

文章图片

论文地址：https://arxiv.org/pdf/1907.12466.pdf
论文作者包括 MIT 数学系助理教授赵宇飞（Yufei Zhao），以及本科生 Yuan Yao 和 Shengtong Zhang、博士生 Jonathan Tidor 和博士后 Zilin Jiang 。

文章图片

中间为赵宇飞。图源：Sandi Miller/MIT Department of Mathematics
赵宇飞于 2017 年 7 月加入 MIT 数学系，担任助理教授。 2010 年赵宇飞获得 MIT 数学和计算机科学双学士学位， 2011 年获得剑桥大学数学硕士学位， 2015 年获得 MIT 博士学位。他的主要研究领域是组合数学（Combinatorics），他对组合数学中的极值、概率和加法问题以及与数学和理论计算机科学其他领域的联系感兴趣。此外他还一直在开发连接图论和加法组合数学的工具。
等角线的数学可以用图论编码。这篇论文为一个被称为谱图理论（spectral graph theory）的数学领域提供了新的见解，并且为研究网络提供了有力的数学工具。其中谱图理论带来了计算机科学中的重要算法，如谷歌搜索引擎 PageRank 算法。
这种对等角线的新理解为编码和通信领域带来了巨大的意义。等角线是「球形编码」的示例，它是信息理论中的重要工具，允许不同方面在一个嘈杂的通信渠道上相互发送信息，如 NASA 与其火星探测器之间发送的信息。