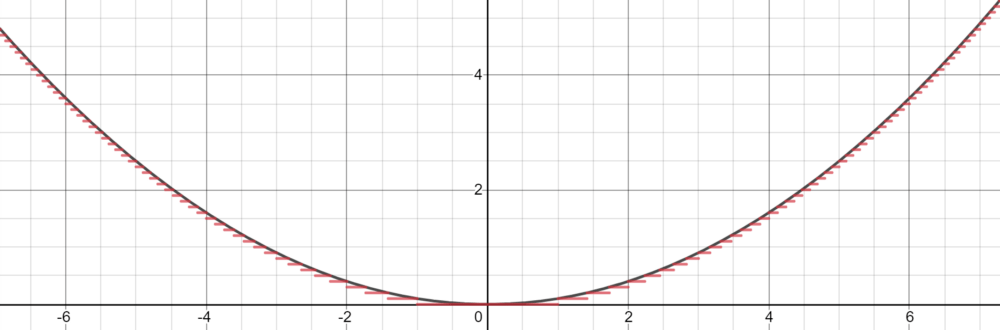
然而 , Cybenko 对这个分段函数描述更为具体 , 因为它可以是恒定 , 本质上通过 step 来拟合函数 。 有了足够多的恒定域 (step) , 我们就可以在给定的范围内合理地估计函数 。
文章图片
基于这种近似 , 我们可以将神经元当做 step 来构建网络 。 利用权值和偏差作为「门」来确定哪个输入下降 , 哪个神经元应该被激活 , 一个有足够数量神经元的神经网络可以简单地将一个函数划分为几个恒定区域来估计 。
对于落在神经元下降部分的输入信号 , 通过将权重放大到较大的值 , 最终的值将接近 1(当使用 sigmoid 函数计算时) 。 如果它不属于这个部分 , 将权重移向负无穷将产生接近于 0 的最终结果 。 使用 sigmoid 函数作为某种处理器来确定神经元的存在程度 , 只要有大量的神经元 , 任何函数都可以近乎完美地近似 。 在多维空间中 , Cybenko 推广了这一思想 , 每个神经元在多维函数中控制空间的超立方体 。
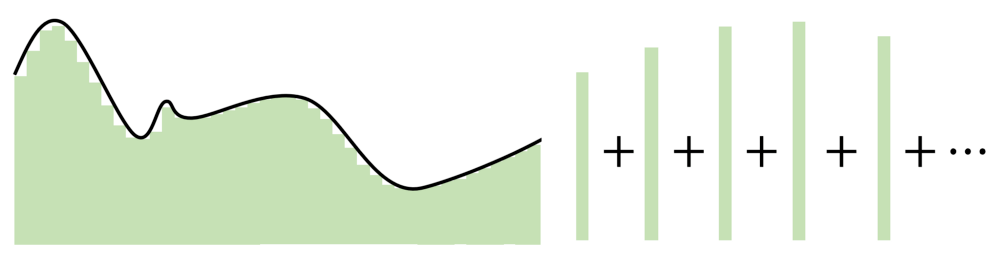
通用近似定理的关键在于 , 它不是在输入和输出之间建立复杂的数学关系 , 而是使用简单的线性操作将复杂的函数分割成许多小的、不那么复杂的部分 , 每个部分由一个神经元处理 。
文章图片
自 Cybenko 的初始证明以后 , 学界已经形成了许多新的改进 , 例如针对不同的激活函数(例如 ReLU) , 或者具有不同的架构(循环网络、卷积等)测试通用近似定理 。
不管怎样 , 所有这些探索都围绕着一个想法——神经网络在神经元数量中找到优势 。 每个神经元监视特征空间的一个模式或区域 , 其大小由网络中神经元的数量决定 。 神经元越少 , 每个神经元需要监视的空间就越多 , 因此近似能力就会下降 。 但是 , 随着神经元增多 , 无论激活函数是什么 , 任何函数都可以用许多小片段拼接在一起 。
泛化和外推
有人可能指出 , 通用近似定理虽然简单 , 但有点过于简单(至少在概念上) 。 神经网络可以分辨数字、生成音乐等 , 并且通常表现得很智能 , 但实际上只是一个复杂的逼近器 。
神经网络旨在对给定的数据点 , 能够建模出复杂的数学函数 。 神经网络是个很好的逼近器 , 但是 , 如果输入超出了训练范围 , 它们就失去了作用 。 这类似于有限泰勒级数近似 , 在一定范围内可以拟合正弦波 , 但超出范围就失效了 。

文章图片
外推 , 或者说在给定的训练范围之外做出合理预测的能力 , 这并不是神经网络设计的目的 。 从通用近似定理 , 我们了解到神经网络并不是真正的智能 , 而是隐藏在多维度伪装下的估计器 , 在二维或三维中看起来很普通 。
推荐阅读
- 星链|石豪:在太空,马斯克和美国当局是如何作恶的
- 建设|这一次,我们用SASE为教育信息化建设保驾护航
- 生活|气笑了,这APP的年度报告是在嘲讽我吧
- 历史|科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 空间|(科技)科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 精度|将建模速率提升10倍,消费级3D扫描仪Magic Swift在2021高交会大显“身手”
- 最新消息|世界单体容量最大漂浮式光伏电站在德州并网发电
- 公司|科思科技:正在加速推进智能无线电基带处理芯片的研发
- 测试|图森未来完成全球首次无人驾驶重卡在公开道路的全无人化测试
- Monarch|消息称微软Win11 2022重大更新将在明年夏天到来







