易坊好文馆

  1. 首页 > 玩科技 >

火箭燃料|其实童年的你离造出火箭只有亿点点距离( 三 )

火箭燃料


02
公式：齐奥尔科夫斯基
剩下的事情会需要一点点微积分 。 我们知道加速度是速度的变化率 ， 那么对时间积分 ， 也就得到了速度的变化量：
其中t0 与tf分别是加速初始时间与结束时间 ， m0 与mf分别是初始质量与末质量 。 这就是大名鼎鼎的齐奥尔科夫斯基公式 。 事实上 ， 他是那样有名 ， 以至于好多时候 ， Δv 成了度量燃料量的标准：不管带了几吨燃料 ， 我只关心我有多少Δv 。 做飞行规划 ， 也更愿意算一步步变轨需要多少Δv 。 事实上火箭的Δv决定了它能飞多远 ， 飞到哪里 ， 是火箭设计中至关重要的量.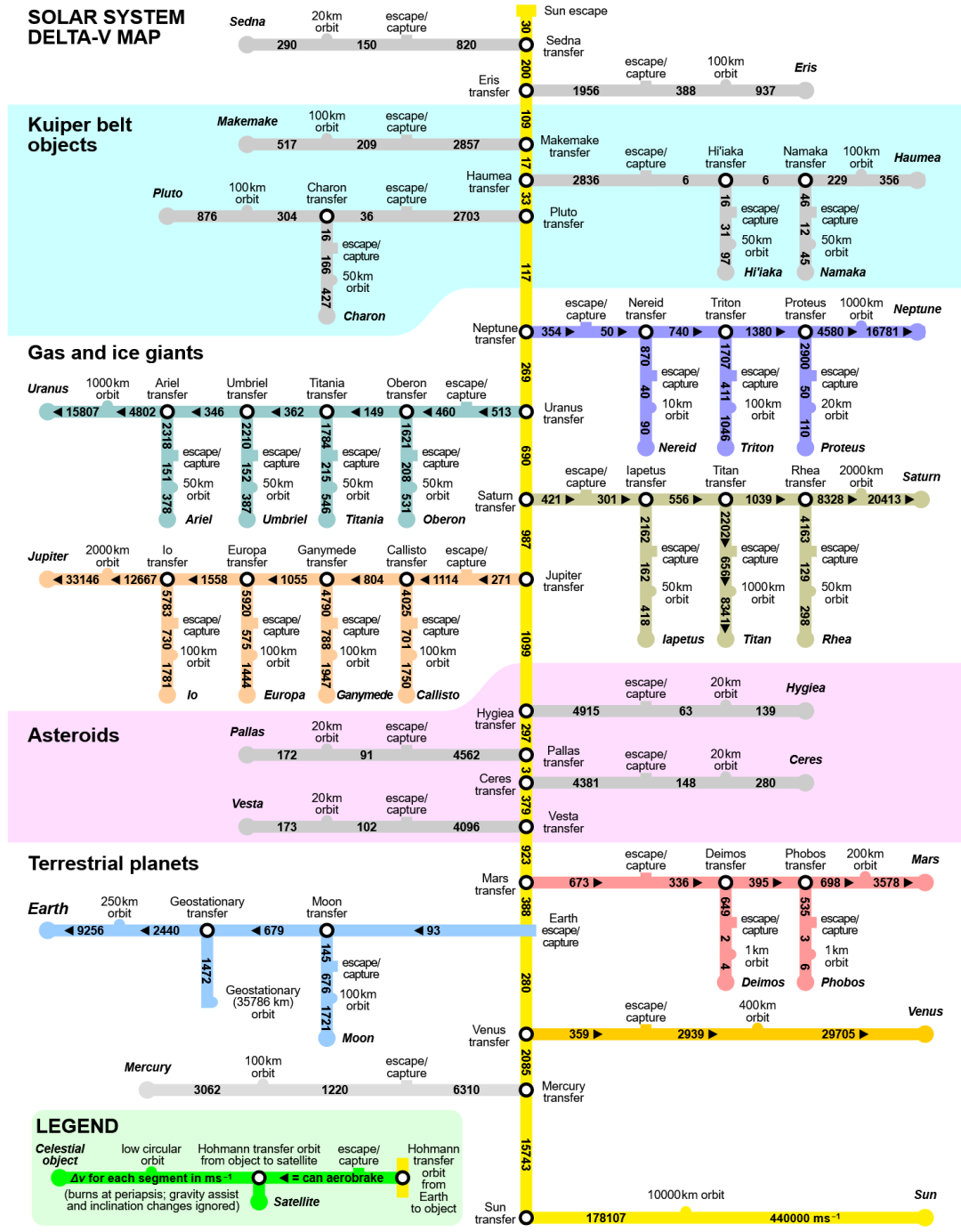

火箭燃料|其实童年的你离造出火箭只有亿点点距离
本文图片

太阳系的Δv地图 。 去不同的地方需要不同的Δv ， 这就像去不同的车站需要的车票价位不同 。 右下角是太阳 ， 从下往上离太阳越来越远 。 来源：wiki
齐奥尔科夫斯基公式告诉我们 ， 无论你飞行时发动机的工作过程是什么样的（对应于不同的R(t)）——比如说可能一直最大油门 ， 或者也许一直都小推力加速 ， 甚至可能干脆让发动机大部分时间关掉——你的可用的Δv都是一样的 ， 它正比于喷口速度ve（或者比冲Isp） ， 也正比于初末质量比（m0/mf）的对数 。 既然初末质量之差就是你用掉的燃料 ， 便可知道火箭飞行需要的燃料要占到总重中非常可观的一部分 。 立在发射场上偌大的火箭 ， 其实大部分都是待消耗的燃料（以及一些没用的死重） ， 真正运输的货物质量 ， 可能不到总质量的2% 。 你想要更多的Δv ， 当然是要带更多的燃料；但是Δv 随燃料量大致是对数增长：多带的燃料固然可以提供加速 ， 但随之而来初始质量的增加 ， 导致同样推力下加速度变小 ， 于是多出来这部分燃料提供的Δv就会变少 ， 加速效果自然会打折扣 。 （只有最后一滴油是最管用的 ， 但是……

推荐阅读


上一篇：最新消息|董明珠与雷军造车殊途：格力先向银隆储能业务下手

下一篇：宇宙起源|如果大爆炸不是宇宙的起点，那会如何？