X = 8 + 15K (K是整数)
这样我们就把寻找的整数解缩小了 , 接着再加入第三个条件 , 找到分别满足X=8+15K和除以7余2的数:
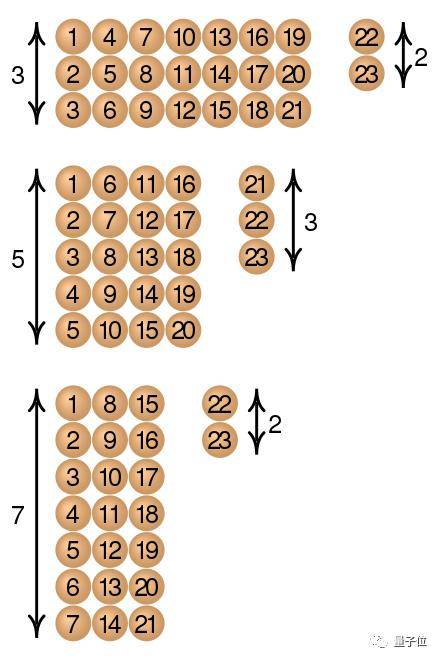
8、23、38、53、68、83、98、113、128……
2、9、16、23、30、37、44、51……
满足条件的第一个数是23 , 第二个数是128 。 后面的每个解与前一个之差都应该是3、5、7的最小公倍数105 。
文章图片
这样寻找解的过程显然太繁琐 。 后来 , 明朝数学家程大位把求解方法编成了一首诗:
三人同行七十稀 , 五树梅花廿一枝 。
七子团圆正半月 , 除百零五便得知 。
意思是:
将除以3得到的余数乘以70 , 将除以5得到的余数乘以21 , 将除以7得到的余数乘以15 , 全部加起来后再减去105或者105的整数倍 , 得到的数就是答案 。
70 × 2 + 21 × 3 + 15 × 2 = 233 - 2 × 105 = 23
其他的解只能和23相差105的整数倍 , 韩信应该是估计出军队大致人数 , 取了105×10+23=1073这个解 。
以上70、21、15几组数到底是怎么来的 , 有兴趣的读者可以进一步阅读“中国剩余定理”的通解 , 在此不再赘述 。

文章图片
这道“韩信点兵”问题不仅仅能用于点兵 , 甚至在天文历法上也有重要应用 。
假设有一颗彗星4年出现一次 , 我们在1991年看到了它、另一颗彗星10年看到一次 , 我们在1997年看到了它 。 我们下一次在同一年看到它们是什么时候?
X ≡ 1991 (mod 4)
X ≡ 1997 (mod 10)
经过计算 , 它们上一次相会是在2007年 , 而且每隔20年重逢一次 , 所以下一次应该是2027年 。
时至今日 , 中国剩余定理已经成为了很多计算机加密算法的基础 , 它的应用范围已经超乎你的想象 。
影响当今计算机算法
外媒Quantamagazine在一篇名为《古代战争计策是如何影响当代数学》的文章中也提到:中国剩余定理对现代数学、计算机算法、天文学等领域都有很大的启发意义 。

文章图片
比如非常有名的RSA加密算法 , 就应用了中国剩余定理 。
我们知道在数论中 , 想要求解出两个大素数比较简单 , 但是想要对它们的乘积进行因式分解就很困难了 。
而RSA加密算法就是把这个乘积作为了自己的加密密钥 。
从1977年诞生以来 , RSA加密算法已经成为了应用最广泛的公钥算法之一 。
此外 , 在快速傅里叶变换(FFT)中也应用了中国剩余定理 , 它可以大大减少计算离散傅里叶变换时所需的乘法次数 。
推荐阅读
- 设计|虚拟世界里的仓颉,竟是我自己?
- the|美国新冠病例激增:老牌香薰蜡烛频遭差评 真相竟是嗅觉失灵
- 警告!|炒币神器现形 竟是庞氏骗局
- 化石|罕见,全球最完整恐龙胚胎亮相福州!成年体竟是是一只“偷蛋”的贼?
- 虚拟|伪概念?真未来?元宇宙究竟是什么?
- 古代|研究揭示东亚家猪遗传历史:黄河流域是独立的家猪驯化中心
- Intel|英特尔Z690主板溢价剖析:LGA-17xx CPU插槽成本竟是LGA-12xx四倍
- AirPods|换个角度看苹果 AirPods,每一代究竟是如何变化的
- 黄彩芝|神秘、新奇的?重点实验室究竟是做啥的?今天为你揭秘
- 库克|究竟是苹果吃相难看,还是另有实情,国产安卓机道出真相








