收敛|NeurIPS 2020 | Double Q-learning的有限时长分析_函数|NeurIPS|问题|Hassel

作者：俄亥俄州立大学五年级博士生熊华清
NeurIPS 2020 文章专题
第·4·期
本文将分享俄亥俄州立大学发表于 NeurIPS 2020的工作：《Double Q-learning的有限时长分析》。
这项工作从理论角度探索了在深度强化学习中有着广泛应用的double Q-learning算法，并首次给出了在有限状态-行为空间（finite state-action space）下该算法的有限时长分析（收敛的时间复杂度）。
通过进一步比较double Q-learning与已有工作中Q-learning的收敛速率，本文还得出了double Q-learning更适合用于高精度任务的结论。通过刻画double Q-learning算法收敛的时间复杂度，本文旨在帮助加深对该算法的理解，并为进一步理解深度强化学习做铺垫。

文章图片

https://arxiv.org/pdf/2009.14257.pdf
一、研究背景
虽然在引言中我们已介绍本文首次给出了double Q-learning (以下用DQL代替) 的收敛速率分析，但这并不意味着该算法是强化学习芸芸算法中的“新贵”或是“无名小卒” 。事实上， DQL是一个已有十年历史，并在深度强化学习中有着极广泛应用的算法。
首先来简单看一下DQL为什么会被提出。从算法的名字，我们很自然会联想到强化学习中最基础最重要的算法之一——Q-learning算法。的确， DQL的提出正与之息息相关。虽然Q-learning已被理论证明可以找到最优策略 (policy)，但在实际应用中，由于采样过程以及回报函数估计中存在的随机性和误差， Q-learning中的最大值函数往往会造成过估计 (overestimation) 问题 (这一点将在算法回顾部分重点分析)，进而可能导致只能学习到次优策略，而DQL就是通过引入双估计器 (double Q estimators) 的办法 (Q-learning采用单估计器) 来有效控制这种过估计问题。
DQL虽然设计思路清晰，应用简洁方便，但却也并非一炮而红。与历史上许多其他模型或算法 (如神经网络) 一样， DQL虽然好用，但也需要一个舞台，一个契机让它进入人们视野，发挥自身价值。在这个契机来临之前， DQL也只能在浩瀚的论文库中默默等待。
2015年底2016年初，由谷歌Deepmind研发的围棋机器人AlphaGo横空出世，击败了李世石九段后，随着AlphaGo一起成为热门话题的，是深度强化学习技术。而AlphaGo中的核心算法—— 深度Q网络 (DQN)，也于2016年初登上了Nature期刊，自此也成为了学界炙手可热的研究课题。除了DQN在Atari游戏和AlphaGo中的大放异彩，还有一个重要契机，便是DQL的原作者Hasselt ，此时正在Deepmind工作。
于是很自然地， Hasselt和David Silver等人也将DQL应用到了DQN中，并重新刷新了几乎所有Atari游戏的最好成绩，也是从这篇论文开始， DQL几乎就成了和DQN如影随形的存在，在实际应用中非常广泛，效果也非常好。
那么问题来了，既然DQL历史也不算短，知名度也不低，为什么之前一直没有收敛速率的理论工作出现呢？除了研究强化学习理论的课题组不多的无奈事实外，还有一个重要因素，那就是与Q-learning相比， DQL的理论分析中有其独特的难点存在。为了理解这些难点，我们首先需要理解算法设计及其思想，特别是理解DQL与Q-learning的差异。
二、算法回顾
接下来我们首先回顾一下Q-learning的算法及其问题，进而理解DQL的设计理念。
Q-learning和DQL都是为了学习得到最优Q函数——Q* ，众所周知， Q*是Bellman方程的唯一不动点 (fixed point) ：

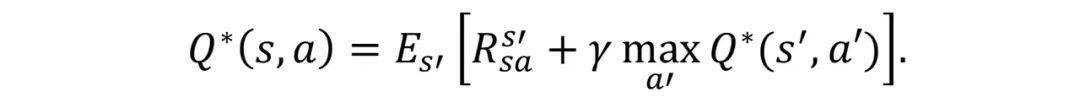
文章图片

在上面公式中， s ， a ， R分别代表状态 (state)，行为 (action)，回报函数 (reward)， s’则表示任务中从 (s,a) 出发得到的下一状态。自然地，我们就可以用解方程不动点的方法得到Q-learning的基本迭代规则：

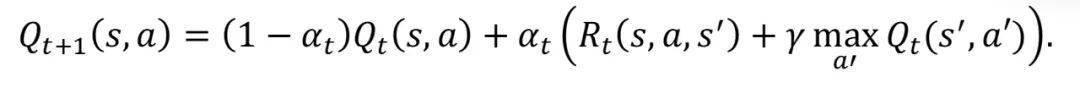
文章图片

在这里，由于期望在实际中不可得知 (因为s’的分布未知)，因此我们通过采样s’来估计回报函数以及每一步中的最优行为a’ 。
在理解Q-learning是一个解方程不动点的算法后，我们来看一下这个算法有什么问题。首先，它的算法设计是清晰简洁的，理论上也被证明了可以收敛到Q* 。但在实际应用中，算法中的最大值函数会带来问题，这就是过估计 (overestimation)。
要理解过估计，首先要意识到Q-learning的最大值函数，事实上是在估计一个求完最大值后的平均值，而Bellman方程中的最大值函数，则是取期望值中的最大值。
举例来说，如果将一些独立同分布的随机变量表示为

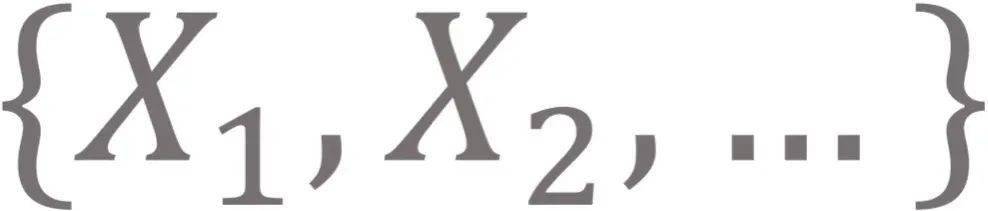
文章图片

，我们希望得到

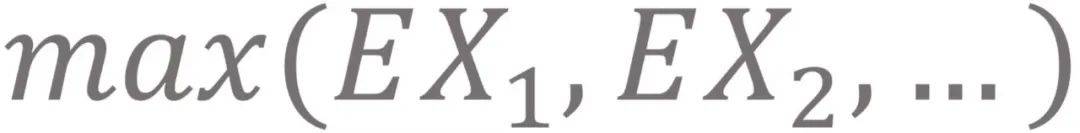
文章图片

，而Q-learning中估计的则是

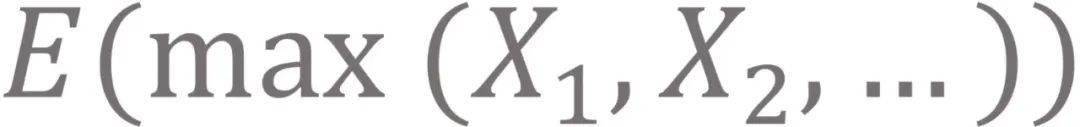
文章图片

。显然，

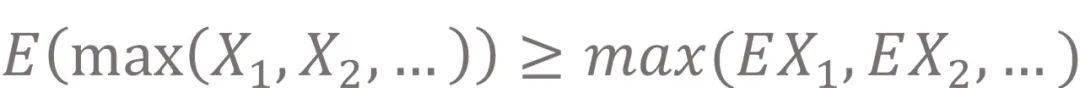
文章图片

。因此，在实际应用中， Q-learning往往会引入正向偏差，也就是过估计。这种过估计，在回报函数估计存在随机误差，或在算法执行过程中存在其他估计误差时，便尤为明显。
上面我们已经分析， Q-learning的过估计问题主要是因为在每一步都采用了最大估计值，那么，由此想到的一个很自然的解决方案，就是避免在每一步都用这么激进的迭代， DQL正是基于此诞生的。下面是DQL的核心迭代步骤：

文章图片

可以看出， DQL每一步还是用了贪心策略，但它引入了两个Q估计器(Q estimators) ，从一个Q估计器中取出最优行为后，却用了另一个Q估计器来得到该行为的Q估计值。比如说，如果当前A估计器被选中更新，并用A估计器得到了最优行为a* ，虽然a*在A估计器中对应最大估计值，但它在B估计器中很可能并非对应最大估计值。
还有一点，那就是每一步A估计器和B估计器被随机选中的概率是一样，所以可以认为这两个估计器是对称迭代的。综合以上两点，可以预计DQL在迭代过程中避免了每一次都用最大估计值，也因此可以改善过估计问题。
三、结果及分析
本文首次对DQL算法进行了有限时长分析(或非渐进分析)。目前针对DQL仅有的渐进收敛 (asymptotic convergence) 分析并不能刻画出算法的收敛速率，因而能提供的理解也很有限。有限时长分析关注的恰恰就是收敛速率问题，只有刻画出了收敛速率，我们才能对算法的设计有更多的理解，才能对不同算法进行比较。这种收敛速率的刻画，可以想见也比渐进分析难度更大。
接下来，我们主要介绍一下基于理论结果的引申讨论。由于DQL是改进Q-learning算法而来的，将两者的理论结果进行比较，也自然是理解DQL的重要途径。
通过比较DQL和Q-learning在相同条件下收敛到最优解邻域的时间复杂度，我们发现在高精度任务下， DQL与Q-learning收敛速度相当，而在低精度任务下， DQL收敛速率则要慢于Q-learning 。因此，本文也指出DQL更适合应用于高精度的任务。
这个结果并不意外，从算法设计中，可以看出Q-learning每一步都用最大值函数实现了贪心策略，这是一种更激进的迭代方法。与之相对的， DQL每一步则有意避开了这种激进的迭代，转而用一种相对“消极”的贪心策略，在贪心策略本质没有改变的情况下，收敛速度放慢也在意料之中。
四、未来工作展望
有关Q-learning ，前后有近三十年不间断的理论研究，相较于此，有关DQL的理论理解仍处于起步阶段，因此也有着更多的潜在问题，比如DQL在状态-行为空间很大甚至无穷时的收敛性问题。
在状态-行为空间极大时， Q估计器不再能由表格函数表示，此时往往需要用一些参数函数 (如神经网络) 来估计Q函数并迭代。可以看出这种设定更接近如今在DQN中广泛使用的DQL ，因此该设定下的收敛性分析也自然非常重要。然而，这种设定下的分析难度也将进一步变大，有待未来更多的探究。
//
作者介绍：
【收敛|NeurIPS 2020 | Double Q-learning的有限时长分析】熊华清，俄亥俄州立大学五年级博士生 (联合导师：俄亥俄州立大学梁颖斌教授，南方科技大学张巍教授)，此前于2016年7月从浙江大学控制科学与工程学院获得学士学位。他目前的研究方向包括强化学习算法，加速算法的收敛性分析，以及非凸优化理论等。

收敛|NeurIPS 2020 | Double Q-learning的有限时长分析

推荐阅读

昆士兰大学的入学要求

注意！不要吃没有成熟的柿子（水果食疗）

卤煮火烧的火烧是什么

林峰收复鬼画是哪一集

古代传统流传的象驮宝瓶吉祥图案有什么寓意？

北青网娱乐综合钟镇涛迎68岁生日获好友刘嘉玲晒合照送祝福

阳痿早泄对男性有什么危害？阳痿早泄对男人的危害有哪些？

药方槐花散治疗什么呢？槐花散功能主治

有关追时尚的名言，有关穿衣打扮的名言或警句0到20句怎么写

地震的前兆是什么地震的前兆是什么现象

凉拌海带丝怎么会有拉丝呢

东莞凤岗镇预防接种疫苗预约方式东莞市凤岗镇防疫站

皮相好骨像差是啥样的体验?

洛阳杜康怎样？

肌肤美白的九大方法

大气层中的臭氧层的作用是吸收？

狗玩具买回来要洗吗

钉钉企业怎么注册

大连新闻网我市查获高速快艇休渔期非法捕捞案

洗脸水中加4种料抗衰老蜜蜂润肤