作者:清华大学五年级博士生 林子钏
NeurlPS 2020 文章专题
第·5·期
本文将分享 清华大学联合斯坦福大学发表于NeurIPS 2020的工作: 《基于模型的对抗元强化学习》 。
元强化学习可以从大量的训练任务中学习并快速地适应于新任务 。 但目前的元强化学习对任务分布偏移非常敏感——当测试任务的分布与训练任务的分布不一致时 , 元强化学习的性能会剧烈下降 。
为了解决这个问题 , 本文提出基于模型的对抗元强化学习 , 通过梯度优化的方式寻找对抗任务 , 并在对抗任务上优化模型 。 该算法在几个连续控制基准测试集上的评估 , 证明了其对任务偏移的鲁棒性 , 在训练和测试的样本效率上均优于当前最先进的元强化学习算法 。

文章图片
https://papers.nips.cc/paper/2020/file/73634c1dcbe056c1f7dcf5969da406c8-Paper.pdf
开源代码链接:
https://github.com/LinZichuan/AdMRL
一、背景
近几年来 , 元强化学习越来越受到关注 。 与普通的强化学习任务不同 , 元强化学习希望通过在训练任务上学习共享的知识结构 , 使算法能够在测试任务上进行快速地泛化 。
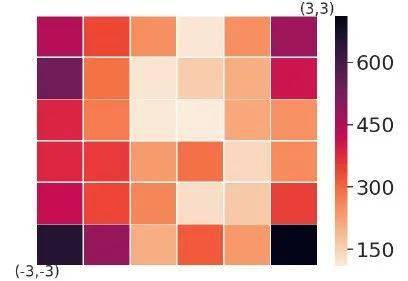
然而 , 现有的元强化学习算法还面临着诸多挑战 , 其中一个挑战就是对任务分布偏移的敏感性 。 在现有的框架下 , 大部分算法会假设训练任务和测试任务是来自同一个分布 。 因此 , 当测试任务的分布发生偏移时 , 算法的性能就会剧烈下降 。 如图1所示 , 我们将当前最先进的元强化学习算法PEARL在Ant2D-velocity任务上进行了测试 , 实验结果证明 , 当测试任务发生偏移 (从中间的格子逐渐偏移向四周) 时 , 算法的泛化性能剧烈下降 。
文章图片
图1 :PEARL算法在Ant2D-velocity任务上的泛化性能 。 颜色表示泛化能力与最优解之间的差距 。 浅颜色代表泛化性能好 , 深颜色代表泛化性能差 。
二、方法
1. 动机
既然传统的元强化学习对手动设定的任务分布比较敏感 , 那我们何不抛弃任务分布 , 让算法本身去寻找自己需要学习的任务呢?沿着这一思路 , 我们进一步思考:我们需要的是一个对任务分布偏移具有鲁棒性的模型 , 因此 , 我们关心的是模型在最坏情况下的泛化性能 。 如果模型在最坏情况下的泛化性能能够得到保证 , 那么对任务分布的偏移就有比较强的鲁棒性 。
2. 对抗元强化学习
为了优化模型在最坏情况下的泛化性能 , 我们首先形式化对抗元强化学习框架 。 考虑一族参数化的MDP任务 , 这些任务共享相同的状态空间、动作空间、转移概率 , 不同的任务对应不同的参数化奖励函数 。 与之前的元强化学习算法 (MAML, PEARL) 共享策略 (policy) 不同 , 我们在不同任务之间共享环境模型 (model)。 我们用 θ表示策略参数 , 用ψ表示任务参数 , 用?表示模型参数 , 用
【模型|NeurIPS 2020 | 基于模型的对抗元强化学习】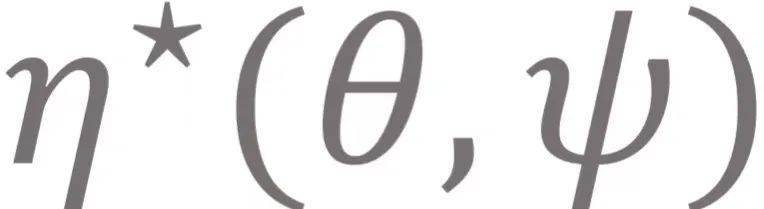
文章图片
和
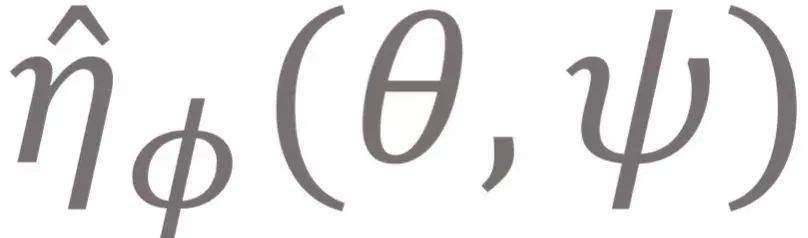
文章图片
表示给定任务ψ策略θ在真实环境 (environment)中以及虚拟环境 (model)中的性能 。
给定任务ψ , 我们可以与model交互学习出一个策略
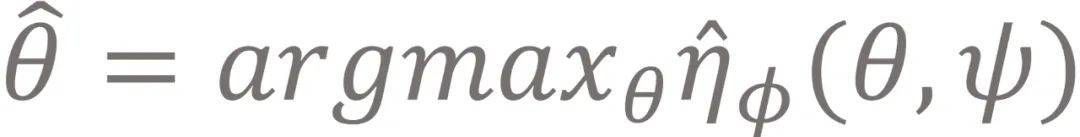
文章图片
。 该策略与最优策略之间的性能差距 , 我们称为次优差距 (sub-optimality gap) , 定义为
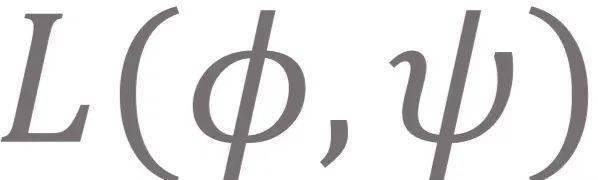
文章图片
。 回顾之前所讨论的 , 我们的目标是为了优化最坏情况下的模型泛化性能 , 换句话说 , 我们希望最小化模型在最坏情况下的次优差距 。 因此 , 我们把该目标形式化为minimax的优化目标如下:
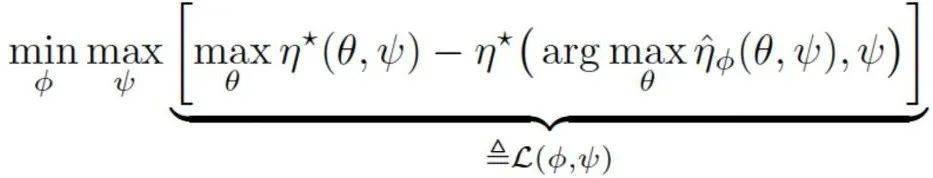
文章图片
在 max这一步中 , 我们调整任务参数最大化次优差距 , 希望找到一个对当前模型来说最困难的任务;在 min这一步中 , 我们训练模型 , 缩小在当前任务上的次优差距 。 通过不断的交替迭代 , 在每一步训练中 , 任务可以通过自身的参数调整 , 为模型的优化带来更大的信息量 。
为了优化上述的minimax目标函数 , 我们需要交替地进行min和max的优化 。 给定某个任务ψ时 , 模型的优化可通过MBRL (model-based reinforcement learning) 求解 。 反之 , 为了优化任务ψ , 我们需要参数ψ对进行求导 , 导数如下:
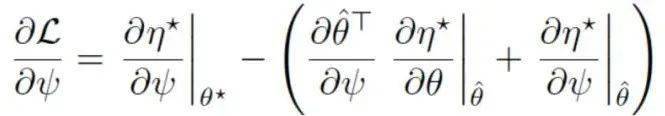
文章图片
为了更高效地求解该梯度 , 我们利用隐函数定理推导出了一个梯度形式 , 并用共轭梯度下降法做了高效率的实现 。 感兴趣的读者可以前往论文链接看推导过程和具体的实现细节 。
3. AdMRL算法
基于对抗元强化学习框架 , 我们实现了AdMRL算法 , 如下方图2所示 。 在每一轮迭代中 , 我们首先用模型训练出策略 (line 3-4), 接着用SLBO算法 (一种MBRL算法) 与真实环境交互迭代优化策略和模型 (line 5-7), 最后我们更新任务参数以增大次优差距 (line 8-12), 供下一轮迭代使用 。

文章图片
图2: AdMRL算法
三、实验结果
1. 性能比较
我们在标准的基准测试集上进行了实验 , 与MAML , PEARL及其变种进行了性能对比 。 在训练阶段 , AdMRL只用了MAML的1%(PEARL的20%)的训练数据 , 尽管如此 , 我们的算法在所有环境上均超过了基线方法 。

文章图片
图3: AdMRL与MAML , PEARL及multi-task policy在测试阶段的性能比较
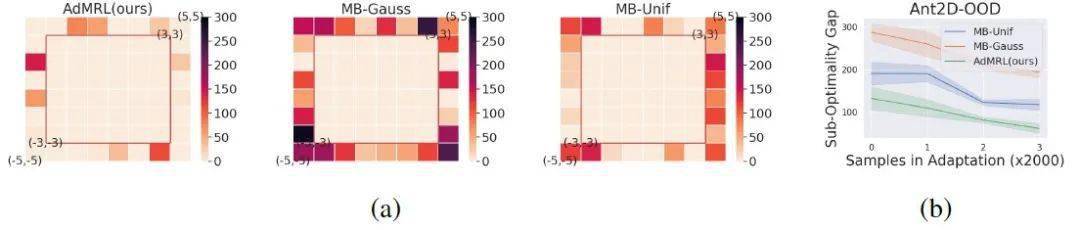
2. 最坏情况下的次优差距的对比
我们与基于模型的方法 (MB-Gauss, MB-Unif) 进行了对比 。 MB-Gauss、MB-Unif分别从高斯分布和均匀分布采样任务来进行模型学习 。 可以看到如图4 (a) 所示 , AdMRL算法在所有的任务上表现得更均匀一些 , 而MB-Gauss和MB-Unif则会过拟合到中间的简单任务上 , 这表明我们的算法对任务的分布偏移更为鲁棒 。 图4 (b) 显示随着adaptation过程的进行 , AdMRL算法能够更快地缩小在测试任务上的次优差距 。
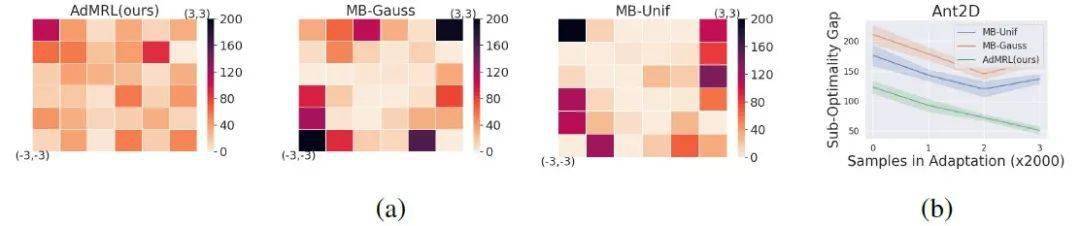
文章图片
图4: 与MB-Gauss和MB-Unif的次优差距对比
3. 可视化
我们在Ant3D环境中将算法优化过程中的任务参数进行了可视化 , 如图5所示.我们发现 , AdMRL算法可以很快地找到较难的任务 , 而随机采样任务的方法(MB-Gauss和MB-Unif)则游离在参数空间中 , 无法准确定位到困难的任务 。
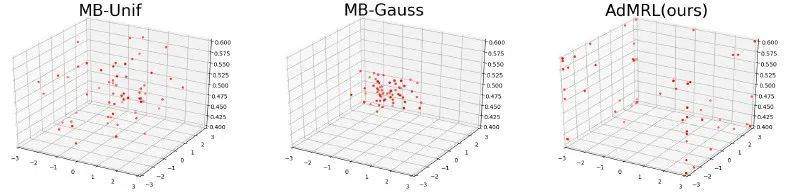
文章图片
图5: 任务参数可视化
4. 分布外 (out-of-distribution) 任务的泛化性能
我们也测试了AdMRL在分布外任务的泛化性能 。 图6展示了与MB-Gauss和MB-Unif的性能对比 , 结果表明 , AdMRL对分布外任务也具有更好的鲁棒性 。
文章图片
图6:AdMRL对分布外任务也具有更好的鲁棒性
//
作者介绍:
林子钏 , 清华大学五年级博士生 。 他目前的研究兴趣是深度强化学习中的样本效率、鲁棒性、可解释性 , 以及深度强化学习在任务型导向对话系统上的应用 。
更多信息请访问个人主页:
http://linzichuan.github.io
推荐阅读
- 模型|2022前展望大模型的未来,周志华、唐杰、杨红霞这些大咖怎么看?
- 平板|小新 Pad Pro 2020 平板开启 OTA7 ZUI 13 灰度推送
- 国际|特奖得主任队长,清华夺冠NeurIPS 2021国际深度元学习挑战赛
- 模型|经逆向工程,Transformer「翻译」成数学框架 | 25位学者撰文
- 化纤|JXK STUDIO 虎年肥猫 1/6仿真动物模型手办可爱摆件
- 模型|达摩院2022十大科技趋势发布:人工智能将催生科研新范式
- 模型|李彦宏:中国迎来AI黄金十年,集度汽车机器人明年亮相,智能交通10年内解决拥堵
- 国际|2020年我国产出卓越科技论文46万余篇
- 模型|神经辐射场去掉「神经」,训练速度提升100多倍,3D效果质量不减
- 排名|2020年我国国际顶尖期刊论文数量排名世界第二 上升2位










