生命的哪些特征是由物理学定律决定的 , 又有哪些特征只是由掷色子般的偶然事件决定的呢?在提及生命及其演化时 , 这仍然是最突出且最有趣的谜题之一 。 英国爱丁堡大学天体生物学家Charles Cockell为本科生定下的一个小课题“研究瓢虫身上的物理定律”进一步让我们相信:地球生物看似极为丰富多样 , 但背后都遵循着适用于所有物质的简单原则 。
本文经授权摘选自《生命的实验室》(中信出版社)第四章“瓢虫与物理学” , 有删节 , 标题为编辑所加 。 点击“返朴”公众号文末“原文链接”可购买此书 。 前往“返朴”公众号 , 点击“在看”并发表您的感想至留言区 , 截至2021年2月27日中午12点 , 我们会选出两条留言 , 每人赠书一本 。
撰文 | Charles Cockell
翻译 | 张文韬、叶宣伽、张雪
我们院系向本科生开设了一门名为“小组合作项目”的课程 。 在这门课上 , 我们鼓励学生们找到他们感兴趣的研究课题 , 并用一个学期的时间来深入探究 , 希望他们从中学到一些新的东西 。
把研究对象从生命群体转向某个单一生命体 , 探究哪些科学定理和方程默默支撑着生命的运转 , 我觉得这是一个好的研究课题 。 2016年冬天 , 我为我指导的研究小组定了一个小目标 , 用几个月的时间研究瓢虫身上的物理定律 。 具体来讲 , 他们需要认真观察瓢虫的每个身体部分和它们生活的各个方面——它们保护翅膀的背壳有多硬?瓢虫是怎样呼吸的?它们如何在草丛间飞翔 , 又如何在叶片上爬动?然后 , 我会让他们写下塑造瓢虫身体结构的物理定律和方程 , 并解释这些方程是如何与瓢虫的生活习性息息相关的 。 概括地讲 , 我希望我的研究小组去探究如何用物理定律和方程式去解释一只瓢虫的一切 。 这并不是一个简单的工作 , 早在我给学生们布置这个任务的时候 , 我就知道这个课题涵盖的知识面极其广阔 , 我随手就能列出一堆其中必然涉及的相关物理知识 , 比如空气动力学、扩散、移动 , 或是热惯量 , 等等 。 果不其然 , 这个课题带给学生们一段独特的体验 , 帮助他们从多方面理解了生命中的物理学 。
让我们从瓢虫的腿开始说起 。 虽然看上去很简单 , 但在这微小的肢体中暗含着无数奇妙的物理知识 。 瓢虫的每条腿上都有3个关节 (人只有两个) , 这让它们的腿可以扭成许多有趣的形状 。 由于活动的自由度很大 , 所以在关于“怎么放腿”这个问题上 , 瓢虫可以在更大的范围内做出选择 。 瓢虫的脑袋里就像有一台电脑 , 它不停地工作 , 结合风速、 接触物表面的平滑度、叶片的大小等所有需要考虑的细节 , 决定如何移动或是摆放这6条异常灵活的腿 。
对于瓢虫来说 , 迈出的每一步都得保证自己抓住表面 (比如抓住游客竖直的手的时候), 不然它就会掉下去 。 与蜘蛛、蜥蜴或其他种类的甲虫一样 , 瓢虫的足底有一层由细毛组成的软垫 , 这层细毛被称作刚毛 , 能够帮助瓢虫或其他生物附着在物体表面 。 瓢虫必须确保刚毛与自己选择的落脚点紧密接触 , 为此 , 它们会从足底分泌出一层非常薄的液体 。 在昆虫的微小尺度上 , 这层液体的黏度和毛细作用可以产生巨大的黏附力 。 与此同时 , 这层液体还能填充瓢虫足底与不平整表面之间的细小空隙 , 使瓢虫像是站在真正的平地上一般 。 这层液体不能太厚 , 只有薄层液体才能提供足够的摩擦力以克服地心引力 , 防止瓢虫从竖直的物体表面滑落 。
结合上述所有关于瓢虫足部和足底分泌黏液特性的新知识 , 我们甚至可以写出一个方程式来定量描述某只瓢虫足部能够产生的总黏附力 。 有了这个方程式 , 我们就可以一窥瓢虫是如何征服各种千奇百怪的地形的 。 我们写出的方程式如下: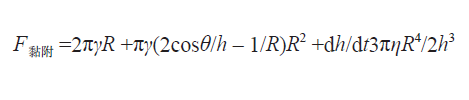
在这个方程式中 , F黏附表示黏附力的大小 , γ 是昆虫足底液体的表面张力 , R 是足底的半径 (为简化计算 , 将足底视作理想情况下的简单圆形) , η 是液体的黏度 , h 是液体的厚度(从昆虫足底至物体表面的距离) , t 是接触的时间 。 等式右边的 3 项从左到右分别代表表面张力、拉普拉斯压力以及黏性力的大小 。
但如果瓢虫想在多变的不规则地形上自由行动 , 还会面临另一个问题 。 对于昆虫来说 , 想要支撑躯干不至于倒下 , 腿必须很坚硬 , 但同时它们也希望腿部能有一些柔韧性 , 这样在一些不规则的物体表面 , 瓢虫才能够更加灵活地移动 。 瓢虫腿部含有的节肢弹性蛋白就是为了达到这个目的 。 节肢弹性蛋白是一种有弹性的生物多聚体 , 这种蛋白能为跳蚤等昆虫提供跳跃所需的弹力 , 也能帮助其他昆虫完成肢体的柔性扭曲 。 节肢弹性蛋白的浓度会随着腿部高度的升高而降低 , 越靠近地面 (靠近肢体末端) 的部分浓度越高 , 保证为跳跃或移动提供弹性;而越远离地面 (靠近躯干) 的部分浓度越低 , 保证腿部足够坚硬以支撑躯干 。 靠近躯干的部分还含有较多的几丁质 , 几丁质是一种坚硬的含氮多糖物质 , 是昆虫其他部分的外骨骼的组成部分 。 几丁质能够增加材料的杨氏模量 , 这种物理量被用来衡量材料的刚性程度 。 在这个例子里 , 我们可以看出 , 为了获得适应各种地形的行动力 , 昆虫的身体结构和物理组成变得更加适应生活环境 。
帮助昆虫黏附在表面的力固然重要 , 但是昆虫也必须能够把腿抬起来——不然 , 瓢虫在落地以后就只能死死地粘在一个位置上 , 徒劳无功地扯动自己的六腿与黏附力做斗争 。 另一个简单的物理公式能够表示出挣脱黏附力所需的能量(W):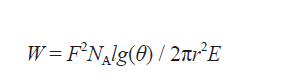
在上述公式里 , NA 是足底的刚毛密度 , l 是刚毛的长度 , E 是刚毛的杨氏模量 , r 是刚毛的半径 。 g(θ) 描述了刚毛与接触物表面的夹角 ,可以通过g(θ) = sinθ[4/3(l/r)2cos2θ + sin2θ]这个公式算出 。
故事到现在还没有结束:昆虫要想附着在物体表面 , 虽然刚毛是必需的 , 但是也不能太多——面积一定的情况下 , 如果刚毛的数量太多 , 它们的排列就会过于紧密 , 不同的刚毛就会卡在一起 。 所以不同的刚毛之间必须保持一定的距离 , 让彼此的相互作用力不至于过大 , 同时在满足上述条件的情况下 , 分布得越密越好 。 下面的方程给出了理论上刚毛能够达到的最大密度: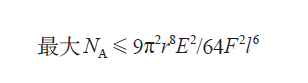
F 是单根刚毛的黏附力 。
在真实情况下 , 昆虫还演化出了许多小花招来增加刚毛的排列密度 。 比如只让刚毛的一侧带有黏性 , 这样就能够大大减少相邻刚毛粘在一起的概率 。 许多昆虫的脚上还长有突刺和结节 , 帮助不同的刚毛彼此分离 。
在演化的过程中 , 昆虫必须要学会这样的技能:既能保证自己牢牢抓住地面 , 又能在想要移动的时候迅速把腿抬起来 。 而昆虫脚上的刚毛恰好是为实现上述生物学功能而产生的 。 不得不说 , 这是一个非常精巧的范例 , 展现了可用方程式表达的简单物理学原则如何精细调整了生命形式 。
其实对于所有的昆虫而言 , 它们的支持器官都必须在“抓紧地面” 与“离开地面”之间取得平衡 , 而只要昆虫具有这样的生理需求 , 它们所需克服的物理障碍就是类似的 。 而对于同样的物理问题 , 所能求得的最优解的数量是有限的 , 所以就算不同的昆虫之间没有相近的亲缘关系 , 各自独立演化 , 最后也会演化出功能相似的生理结构 。 这种现象叫作趋同演化:物理学原理限制了生物学结构的可选择范围 , 所有昆虫都存在某些趋同关系 , 无论它们的结构各自分开来看多么复杂且令人目不暇接 , 从功能上都能被还原到简单的原理 。
像你我这样的人 , 可能一时之间还无法深入理解小型昆虫在墙面这样的竖直表面 , 甚至叶片反面或天花板那样的倒立表面上行走的奇妙之处 。 并不是只要在足底分泌一层薄薄的黏液 , 我们也能够在竖直的墙面上行走了 。 在这个问题上 , 我们必须考虑作用力的尺度 。 以人类的尺度而言 , 重力起到了主导作用 , 在我们迈出竖直攀爬的第一步之前 , 地心引力就会无情地把我们拉回地面 。 可是瓢虫的质量仅仅是我们的25 000分之一 , 在这个尺度上 , 占主导地位的就是像表面张力、毛细作用力、 范德华力这样的分子作用力了 。 正是利用一些影响分子作用力的小技巧 , 瓢虫才得以黏附在墙壁上 。 当然这并不是说瓢虫不会受到重力的影响 , 当它们从墙上或树叶上掉下来的时候 , 它们也会像我们一样落到地面 , 只是速度慢了一些 , 受到的伤害也更小 。 在地球上 , 一切物体都会受到重力的作用 , 只是以大多数昆虫的个头而言 , 分子作用力发挥着主导作用 , 而不是重力 。
然而 , 有得必有失 。 尽管瓢虫可以仅凭借一层薄薄的液体就附着在墙面上 , 但为它带来这些好处的分子作用力和作用定律也同时为它带来了一些不利之处 。 当我们或其他大型动物需要清洁身体的时候 , 我们可以淋浴、泡澡 , 或者直接跳进距离最近的水塘就行 。 在我们结束清洗的时候 , 由于重力的作用 , 大部分水珠都会直接从身上滑落 , 只有一些薄薄的水层或几滴水珠还挂在身上 。 狗会甩动自己的身体把水珠甩走 , 人类会用毛巾把水擦干 。 就算两个办法都不可行 , 只要等待一段时间 , 这些水也能自然蒸发掉 。
在这个问题上 , 瓢虫则需要更小心 , 就算是一小滴水也会死死地粘住它们 。 这滴水所产生的表面张力对它来说太大了 , 即使瓢虫的腿就它们的体积而言已经极为强壮 , 也无法将这团水从自己的身上推开 。 一些体积更小的昆虫 (比如蚂蚁) 甚至完全有可能被一滴水困住 。 水滴表面的水分子之间的吸引力形成了一个由表面张力构成的“水牢” , 将蚂蚁困在水滴的内部无法挣脱 。 由于类似的原因 , 许多昆虫 (尤其是小型昆虫) 会选择通过“干洗”的方式清洁自身 。 它们用自己坚硬的腿刮去身上的灰尘和脏东西 , 避免落入可怕的水之陷阱 。
在现实生活中 , 有许多非常明显的事情 , 我们有时会觉得它们是理所当然的 , 也不会对它们产生过多的兴趣 , 比如苍蝇和瓢虫可以停在竖直的表面 , 而人类却不行 。 不过这个现象却反映出 , 我们和瓢虫生活在两个尺度不同的世界 。 毋庸置疑的是 , 瓢虫的世界和我们的世界共用一套物理法则 , 只不过在不同的尺度范围内 , 占主导地位的是不同的作用力 。 这同一套物理法则解释了生物功能与形态方面的众多现象 。 在我们分析瓢虫腿部的设计、小型昆虫洗澡的方式 , 或者人类与瞪羚运动极限的时候 , 没有任何一个细节是可以忽略的 。 然而 , 光是探索演化中的偶然历史事件 , 无法帮助我们理解演化的极限与可能性 。 如果让演化重来一次 , 生命的模样可能会与现在完全不同 , 那些我们所注重的细节就会失去意义;但是无论如何 , 生命肯定还是遵循着基本的物理学定律 。 所以 , 若是从基础物理学原理的角度去看待和研究生物现象 , 我相信我们能够获得更多根本性的收获 。
……
在这一章里 , 针对这只小小的瓢虫 , 我们进行了一次有趣的探索 。 在这个过程中 , 我们能够体会到物理学与演化之间存在着一种不容忽视的深刻联系 。 在几个月的调研之后 , 我课上的瓢虫物理研究小组上交 一份报告 , 尽管在这份报告里他们只讨论了少数几个物理定律 , 报告的长度就已经超过了 40 页 。 我们甚至没来得及详细探查瓢虫的触须 , 这上面密集排列着各种感受器 , 能够感知化学物质、周围的物理环境 , 在飞翔时体察风速 , 甚至某些昆虫的触须还能识别声音 。 针对这每一种能力 , 我们都能列出一系列方程式 , 并进行深入的分析 。 我们也没来得及讨论瓢虫的进食 , 观察它们的颚咀嚼的力学原理 , 弄清它们如何剪断叶片、碾碎食物 。 进食过程一定包含着数不尽的物理学定理及作用力的参与 , 共同保证了瓢虫的正常生活 。 说到食物的消化和吸收 , 又有一片新的领域能让我们开拓:扩散、渗透 , 以及摩擦力 , 这些和其他作用力一起决定了昆虫对于能量和营养物质的吸收效率 , 而这对于它们的成长和繁殖是不可或缺的 。 还有昆虫的血液——血淋巴 , 它在微小的血管中循环 , 为细胞输送营养物质、清除代谢废物 。
还有许多问题可以探索:昆虫的肌肉背后蕴含着什么样的物理学原理?它们如何储存能量?它们的外壳蕴含着怎样的细节?瓢虫的繁殖又与物理学有什么样的关联?从卵到幼虫再到成虫 , 这些瓢虫发育的各个时期呢?如果想要完全弄清楚这些问题 , 我想可能还需要三年甚至更多的时间 。 上面这些问题不属于本书的讨论范围 , 但是本章中简要探索的几个方面已经足以支持我们的结论了 。
我们看到 , 瓢虫是一种极其复杂的生物 。 虽然它的质量仅仅只是太阳质量的 1033 分之一 , 但这小小的身躯里利用的物理学定律比解释恒星的结构和演化所需的物理学定律还要多 。
这些物理学定律彼此间并不是独立的 , 而是互相影响的 。 在演化的过程中 , 自然选择作用于每一个生物 , 没能成功利用这些定律尽可能促进繁殖的个体将会被自然淘汰 。
以瓢虫的背壳为例 , 它们微米级别厚度的翅膀必须使其安然度过一生中无数次的碰撞 , 任何一次意外都有可能撕裂和破坏它们 。 所以瓢虫需要坚硬的厚壳 , 帮助它们应对户外生活的撞击和种种意外情况 。 不过 , 若是背壳过厚 , 负重过高 , 将会影响瓢虫的飞行 , 让它们在遇到捕食者时不能灵活迅速地逃离危险 。 面对这样的难题 , 瓢虫选择了几丁质这样一种材料 , 这种材料的杨氏模量决定了它的刚性 , 适用于涉及空气动力学中的方程的计算 。 但是同时 , 瓢虫的背壳还需要考虑热量因素 。 几丁质在吸收热量之后强度会发生变化 , 这就直接将瓢虫体温的方程式与材料应对碰撞的有效程度联系到了一起 。
我们可以想象 , 有这样一张大纸上写满了好几百个与瓢虫相关的物理公式 , 上面还画满了箭头 , 标示着不同方程的项或者解之间的相互关系 。 在这样一个网络中充满着大量的反馈机制 , 一个方程出现改变 , 和它相关的其他方程也会随之改变 , 就像往水中丢下一个石子 , 周围泛起涟漪 , 层层扩大 。 这就是生命 。 突变会改变一些方程的解、引入新的方程 , 或去掉一些已有的方程 , 虽然只改了几处 , 但由于这些方程之间彼此缠结 , 将会造成整体的改变 。 自然选择作用于整个互相缠结的系统 ,迫使其适应环境 , 那些能够帮助瓢虫繁育的图纸将会保留下来 , 那些不能的将会被淘汰 。
我们可以把所有关于瓢虫的物理定律都输入计算机 , 然后模拟合成一只瓢虫 。 当然我们在本书中进行的探讨还太过粗略 , 比如除了宏观上的物理学定律 , 我们可能还要深究基因层面的变化 , 考虑基因发生的突变和错误 。 在更高层面上 , 我们甚至能够合成一群瓢虫 , 模拟它们聚集成群以度过寒冬的模式 。 我们试图将一个完整的多细胞生物还原为一些可以用方程式来表示的物理学定律的集合 , 这种尝试不仅有科研上的用途 , 还能帮助我们深刻地理解塑造生命形式的多种多样的作用力和可能性 。 通过对这种规律的不断探索和理解 , 我们甚至能够拥有一定的预测能力 , 而这种能力 (总结规律并进行推测、假设) 是科学的本质特性之一 。
我们可以将生命简化成一组方程 , 这种方法有效地将遗传学和物理学联系在了一起 。 以瓢虫的体温为例 , 决定其体温的热量方程中的参数都可以看作是由基因调控的 , 有可能是一个基因、一组基因起作用 , 或者是许多基因共同调控的结果 。 昆虫背壳表面损失的太阳辐射热量取决于背壳反射的能量 , 背壳反射的能量多少取决于背壳的光亮程度 , 而背壳的光亮程度则是基因和发育信号通路的产物 , 基因和发育信号通路决定了瓢虫背壳的表面物理性质 。 如果背壳的表面是粗糙的 , 还会有一些热辐射发生散射 , 这个性质同样也受到调控背壳的基因的影响 。 昆虫自身损失的热量又取决于背壳的厚度 , 这也是控制发育过程的基因调控的 。 后面的推理同上 。
在处理这些参数时 , 我们要注意不能将这些方程具体化 , 因为它们的存在不同于物理实体 , 它们只是描述了不同变量之间的关系 。 然而 , 方程定义了帮助生物活到繁殖年龄的某种特性 (如热平衡) , 我们可以把它看作将有机体的多种物理特性结合在一起的方式 。 在这种情况下 , 组成这个方程的各个项的特征 , 可以被归为某一个或某几个特定的基因 , 或是它们产物之间的互相作用 。
通过把方程中的每一项和其具体对应的基因或生物学通路联系在一起 (举一个简单的例子 , 我们可以把热量平衡公式中有关背壳厚度的项替换为决定瓢虫背壳厚度的基因) , 我们甚至可以用某一基因的活性来表示方程中的某一变量 。 用这种方法 , 我们真正地将宏观世界中的物理关系或性质 , 与微观世界中导致该种宏观现象的基因组或生物学通路整合在了一起 。
为了确定环境如何影响了生命体为特定方程式选择的解 , 我们还需要探究不同环境对生物遗传学通路的影响 。 这样 , 我们就可以把整个进程整合起来看 , 一方面是宏观的物理学定律自上而下地发挥作用 , 另一方面是基因自下而上地决定了每一种结构的形态 。 本质上来说 , 方程是一种有用的手段 , 它可以告诉我们一个生物的哪些特性能够被当成一个小整体去看待 , 方程中不同的项可以共同决定某一种帮助生物到达繁殖年龄的性质 。 许多基因会参与多个生物进程 , 同时发育过程也非常复杂 , 将遗传学和物理学联系在一起将会是一项极富挑战性的工程 , 毕竟并不能简单地将单个基因与单个表型特征相对应 。 然而 , 不管我们怎么看待演化物理学或物理遗传学 , 它们确实为我们提供了一种有用的思考方式 , 将生物学中的演化、适应概念与定量的、受物理学限制的项结合在了一起 。
【瓢虫|瓢虫为什么不敢用水洗澡?丨展卷】通过这章中简单探讨的例子 , 我们得以一窥趋同演化 (亲缘关系很远的生物拥有类似的结构) 产生的普遍缘由:相似性取决于共同的物理定律 。 无论是黏性的、长着刚毛的足 , 翅膀的形状 , 还是背壳的颜色和厚度 , 瓢虫身上的各种结构告诉我们 , 形成这些结构的简洁公式和数学关系其实也适用于所有昆虫 。 这些方程式形成的网络会不断地出现改变和改进 , 翅膀变得更大就会改变背壳或腿部的尺寸 。 甲虫背壳的颜色将会影响热量的调控 , 甚至改变昆虫过冬的习性 。 基于捕食者、食物、 栖息地 , 昆虫被迫不断发生细小的调整 , 也正因此 , 自然界才产生了丰富多彩的昆虫世界 。 然而在这些所有的细节之中 , 起到根本作用的还是那些决定性的方程式 , 这些方程式的存在从某种意义上来说限制了演化的种类和道路 , 它们美丽而丰富 , 且在生命现象中起到了主导性作用 。
推荐阅读
- IT|为什么感染飙升但死亡人数有限?研究显示T细胞可防止奥密克戎引发重症
- 德尔塔|为什么感染飙升但死亡人数有限?研究显示T细胞可防止奥密克戎引发重症
- 生活|2022,你为什么需要一块华为 WATCH GT3?
- 记忆|为什么现在的年度听歌报告,越来越好哭了?
- 符合中国|为什么要注册中文域名?中文域名很好?
- 周建明|周建明:我们为什么要强调基础科学研究?
- 智电|你的纯电MPV,为什么需要一个专业户来操刀?
- 安全|为什么我们现在不再需要杀毒软件了?
- 标准|5G很美丽,也要解好题:为什么今天必须关注5G-Advanced?
- 技术|【冬奥问“冀”】为什么说观众在观赏冬奥会时也能感受到高科技?






