易坊好文馆

  1. 首页 > 生活百科 >

通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明( 二 )


文章插图

  • 图8：虽然宇宙尺度因子a（t）增加了（宇宙的大小增加了），但移动的距离却没有
相应的里奇张量则为：
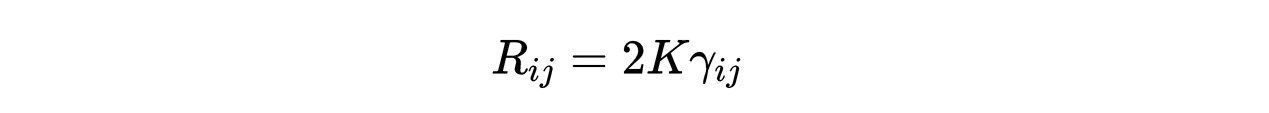
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程4：里奇张量对应于方程3。
我们的宇宙模型是极大对称的。极大对称意味着球对称。从卡罗尔对史瓦西黑洞的讨论中可知：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程5：球对称空间度量可以写成这种形式。
其中r为径向坐标：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程6：二维球上的度规
为了继续，我们将需要引入张量的概念。让我们来考虑一些例子：
零阶张量是一个标量，一个由单个元素（如实数）描述的量。温度是一个标量，因为在某一点它是一个单独的数字。
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 图9：蛋白质片段的热振动幅度随温度升高而增大。
向量是一个一阶张量：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 图10：一个向量的例子
为了理解高阶张量，我们跟随狄拉克，首先建立一个特殊的二阶张量：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程7：一个二阶逆变张量的例子。
【通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明】这是一种特殊的张量。在新的坐标系下，x→x’张量T变换为：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程8：方程7中的张量在坐标变换后的变化。
加上几个类似于T的张量，我们得到一个一般张量：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程9：一般二阶张量的一个例子。
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 图11：二阶张量的图解
正如狄拉克所指出的：
关于一般张量的重要事情是，在坐标的变换下，它的分量的变换方式与T相同。
因为有两个上标，这个张量叫做逆变张量。协变张量有两个下标和类似于方程8的变换，但是在分母中有素数坐标（如果流形上的每个点都与一个张量相关，我们就有一个张量场）。张量是写广义相对论方程所必需的，因为如果一个张量方程在一个坐标系中成立，那么它在所有坐标系中都成立。
由于广义相对论遵循一般协方差原则，根据该原则，物理定律的形式不应因我们如何标记时空点而改变，张量的使用是至关重要的。
找到度规让我们回到方程5。下一步是找到与这个度规对应的函数β（r）。为此，我们需要爱因斯坦场方程（EFE），由：
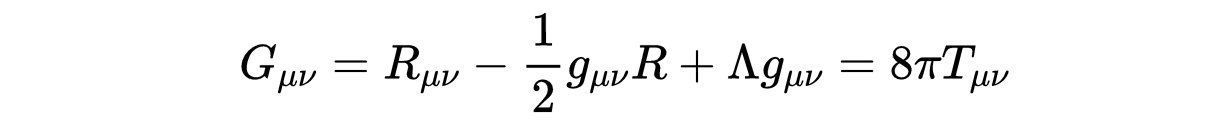
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程10：爱因斯坦场方程。
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 图12：根据爱因斯坦场方程，质量之间的引力效应是它们时空扭曲的结果
这里：
  • 二阶张量R被称为里奇张量，它衡量时空的几何性质（局部）与通常空间（欧几里得）有多少不同。
  • 张量g是度规张量
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程11：出现在爱因斯坦场方程中的度规张量g。
在最简单的情况下，平坦的闵可夫斯基空间，度规张量g为：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程12：平坦闵可夫斯基时空的度规张量。
  1. 标量R是标量曲率R（R的迹）。
  2. λ（宇宙常数）等于真空能量（与暗能量有关）。
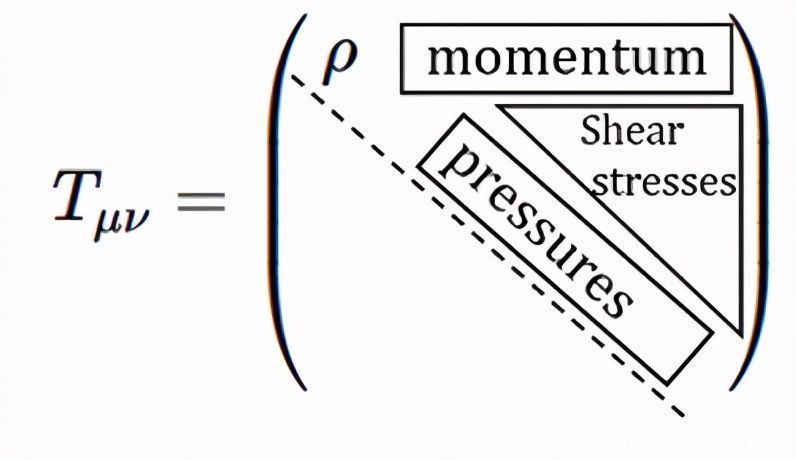
  3. 右边的二阶对称张量T是能量-动量张量，其形式是：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程13：应力-动量张量T的分量。
其中ρ是能量密度。
回到方程5，我们计算张量R的分量，经过一些代数运算，我们得到了以下关于dσ2的表达式：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程14：新的球对称空间度规。
参数k决定空间曲面的曲率，通常归一化为：
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明
文章插图
  • 方程15：参数k决定空间表面的曲率。
通过数学揭秘宇宙的起源，宇宙大爆炸的数学证明

推荐阅读


上一篇：地球如何才能不“碳”气！

下一篇：月球背面地下藏着什么玉兔二号探测结果来了