编码为什么时间被编码在空间几何中？通过理论计算证明( 三 ) 证明|拉格朗日|空间几何|方程

方程18：作用积分。

在ADM语言中，它变成：

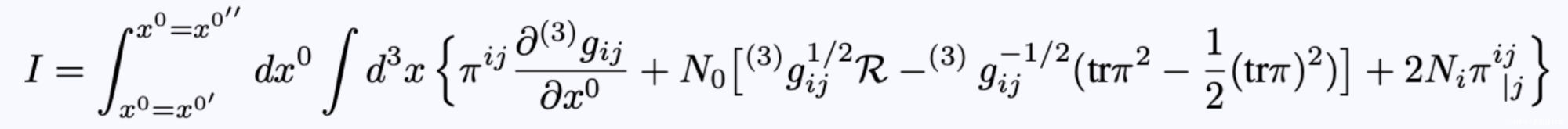
文章插图

方程19：用ADM形式表示的作用积分。

π是几何动力场动量共轭到几何动力场坐标3g，定义为：

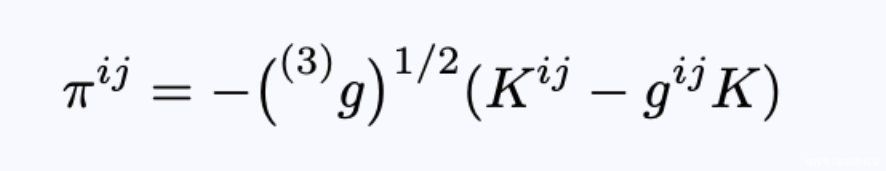
文章插图

方程20：ADM场动量π。

竖条表示三面内的协变导数。
步骤4
现在假设这三个几何图形几乎是相同的。然后,我们有：

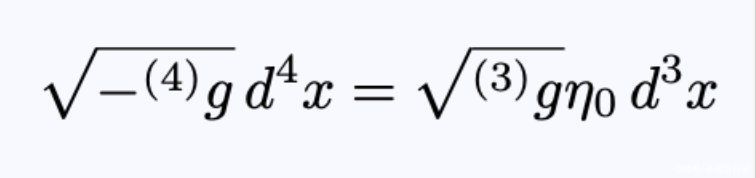
文章插图

方程21：三个几何形状几乎相同时的体积元。

用以下三度规在垂直于曲面方向上的非归一化时间导数来代替外在曲率：

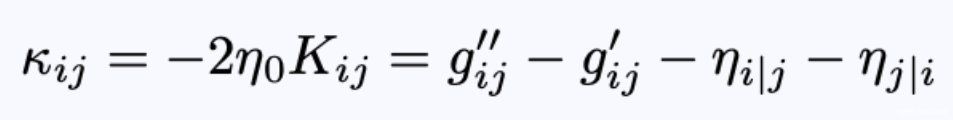
文章插图

方程22：三度规在垂直于曲面方向上的非归一化时间导数。

使用方程21，作用变成：

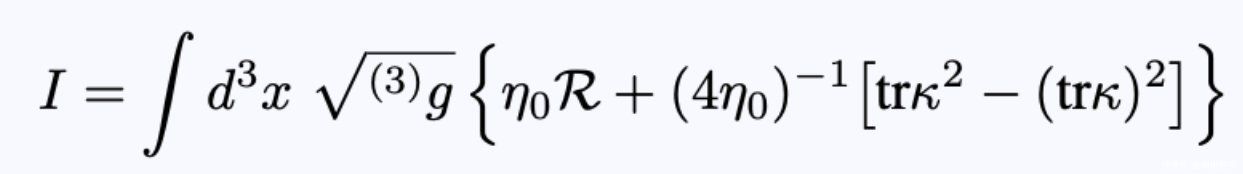
文章插图

方程23：三个几何图形几乎相同时的作用。

步骤5
现在求关于η?的极值，得到：

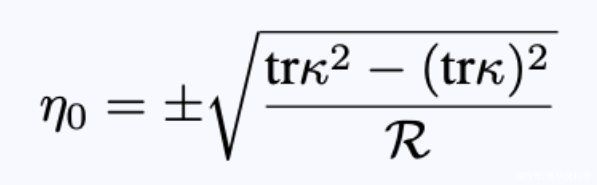
文章插图

方程24：两个三面之间的固有时分离。

这是两个三面之间的固有时间间隔。
步骤6
注意，η依赖于k, k依赖于位移向量η?(x1, x2, x3)，为了得到η?(x1, x2, x3)，把方程22带入到方程23，结果是：

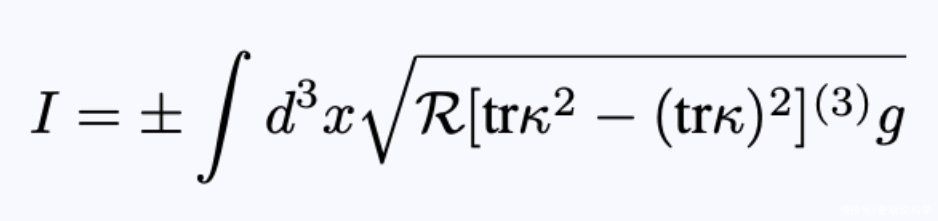
文章插图

方程25：只改变位移矢量分量的运动。

η?被舍弃。然后改变动作I只与分量有关。
步骤7
下一步是求解步骤6中η?的方程，并将其代入方程22和方程24。因此，根据两个三面的固有几何，找到时间间隔η?。
步骤8
【 编码|为什么时间被编码在空间几何中？通过理论计算证明】外部曲率K由式22得到。可以证明，使用爱因斯坦场方程与初始的三度规和外在曲率K一起确定表面嵌入的时空的度规。因此，BSW展示了如何找到两个表面之间的时间间隔，以及它们在给定的两个三维几何图形中的时空位置。