编码 为什么时间被编码在空间几何中?通过理论计算证明

文章插图
在爱因斯坦广义相对论(他的引力理论)的原始公式中,基本场是度规张量g,这个理论在时空中是协变的。协方差由“物理定律在任意坐标变换下的形式的不变性”组成。这个想法是,由于坐标只是人造的标签,物理定律不应该取决于它们选择的方式。
在广义相对论中,这种运动(一个系统动力学的一个属性,从这个属性可以导出它的运动方程)被称为爱因斯坦-希尔伯特运动: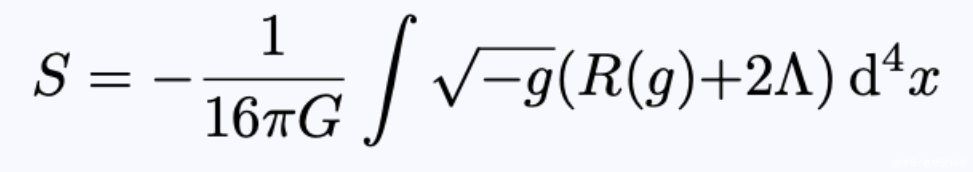
文章插图
- 方程1:爱因斯坦-希尔伯特作用

文章插图
- 爱因斯坦和希尔伯特。
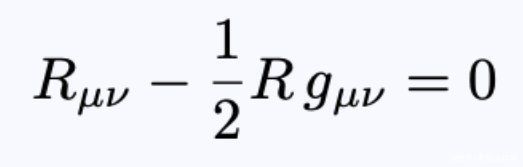
文章插图
- 方程2:无物质条件下的爱因斯坦场方程。
用粒子力学作类比可能有助于阐明这些观点。在拉格朗日力学中,我们给出一个拉格朗日L,我们构造一个作用泛函S,通过对S求极值得到运动方程:
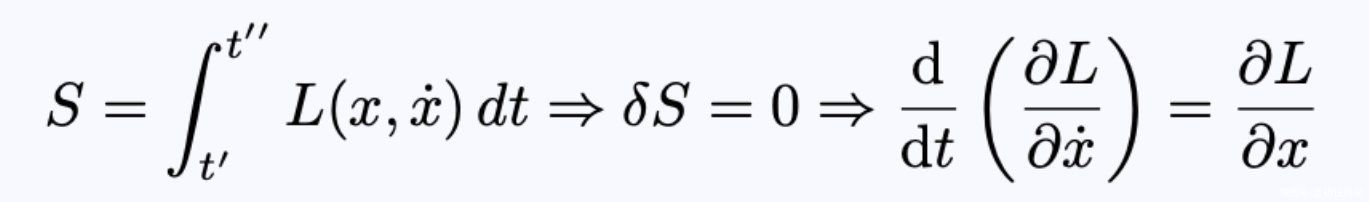
文章插图
- 方程3:给定一个拉格朗日L,对作用函数S求极值,得到运动方程。

文章插图
- 图1:质点选择使运动达到极值的路径。
发生这种情况的原因如下。将方程3中的拉格朗日方法推广到广义相对论,我们将得到:
- 具有内在几何结构的初始三维表面(下面方程4的第一项)。
- 第二个三维曲面也具有相关的内在几何(方程4的第二项)。
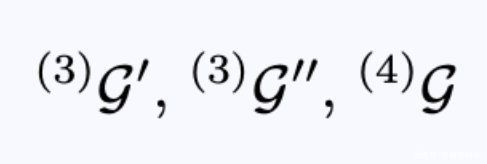
文章插图
- 方程4:上述两个三维曲面的本征几何和四维时空的几何。
- 找出两个三维表面之间的时间间隔。
- 找出这些表面在时空中的位置。
在进一步讨论之前,对所谓的广义相对论ADM形式主义有一个概念是至关重要的。这将是下一节的主题。
ADM形式主义的鸟瞰图在ADM形式主义中,广义相对论被表述为一个动力学理论,以其作者Ricard Arnowitt, Stanley Deser和Charles Misner命名。

文章插图
- 图2:Richard Arnowitt, Stanley Deser和Charles Misner。
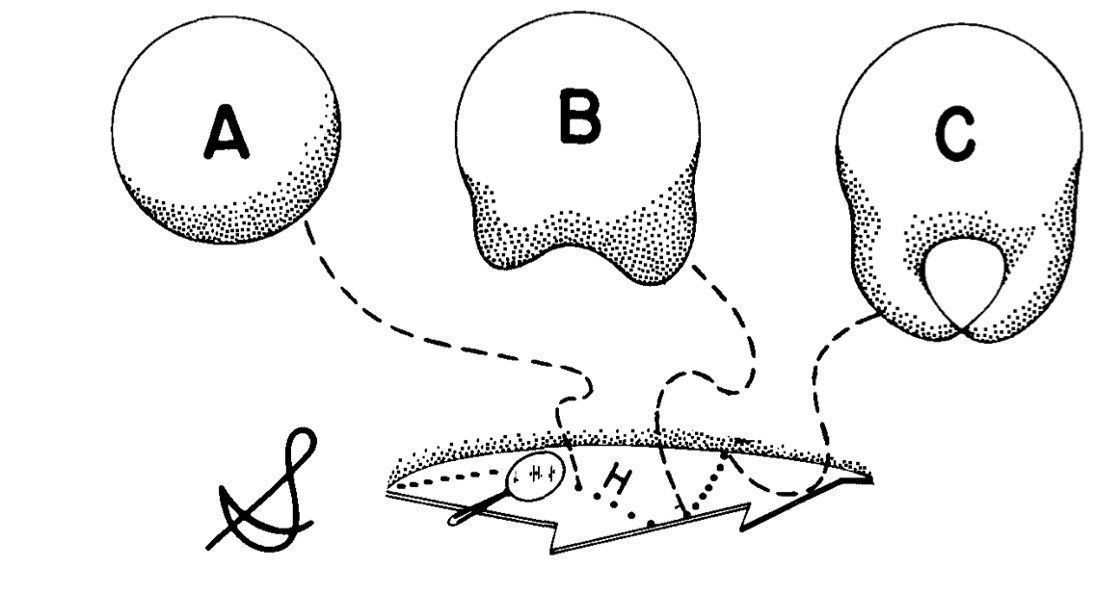
文章插图
- 图3:几何动力学的超空间。
ADM结构如下图所示:
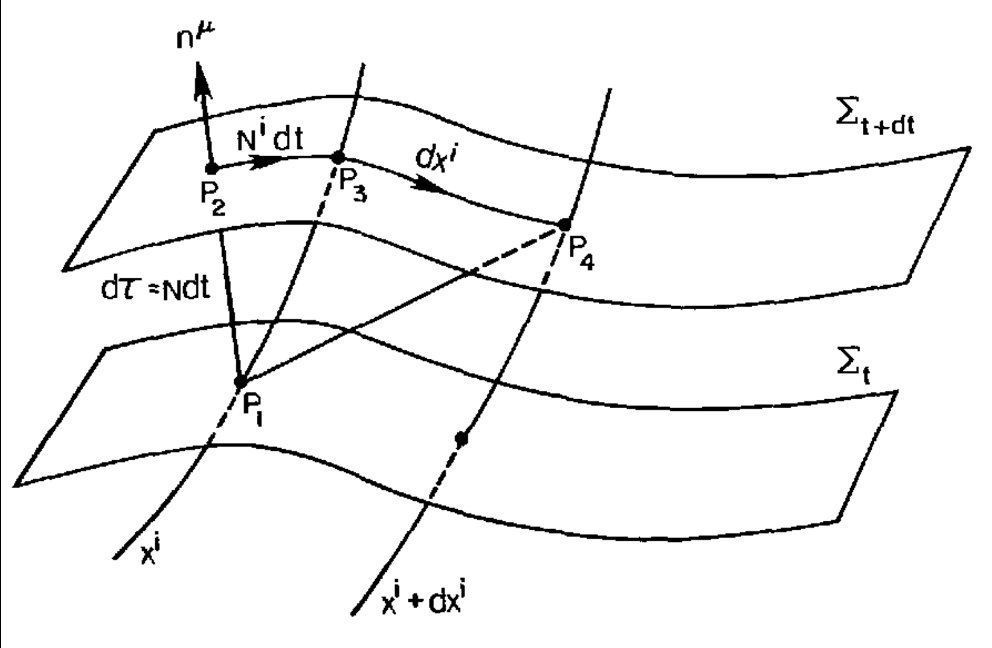
文章插图
- 图4:ADM结构。嵌入四维时空中的两个三维表面(三几何图形)。
使用图2,我们可以用移位和延时来重写ds2:
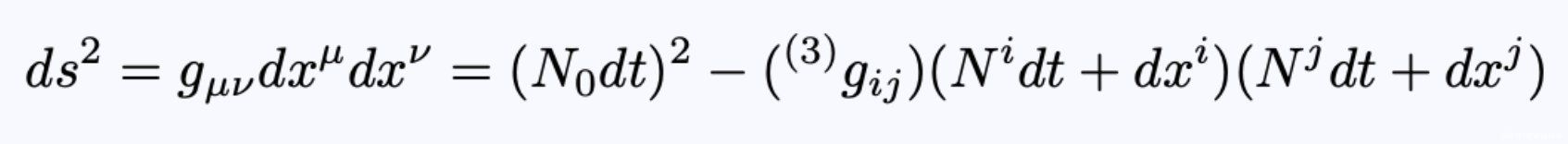
文章插图
- 方程5:P?与P?之间的距离。
推荐阅读
- 初入职场的我们 《初入职场的我们》郑茹心为什么会离开?
- 观众们 《中餐厅5》录制时间曝光,新阵容备受关注,龚俊周也有望合体
- 米兰时装周 王俊凯为什么能被受邀参加米兰时装周的呢?
- 飞行嘉宾 黄渤为什么中途退出《哈哈哈哈哈》?原因很现实
- 信用卡 为什么银行的人,追着你办信用卡?办卡送礼物,到底有什么秘密?
- 生猪价格 生猪价格正在下跌和上涨。为什么上升这么难?终于找到原因了
- 太空港 哈勃望远镜“继承者”又鸽了!发射时间或延期至年底
- 张哲瀚 被问为什么和龚俊总黏在一起张哲瀚的回答,堪称教科书
- 电子商务 亚马逊调整“休息时间任务”政策 批评者此前称该政策限制上厕所时间
- 警告 霍金生前为什么警告人类,要抓紧离开居住的地球他发现什么







