光速|听说一切物体在时空中的速度都是光速c？_相对论|维空间|科技|物理

相信很多人都听过这样一句逼格很高的话：在相对论里，一切物体在时空中的速度都是光速c 。
有些人还会把“在时空中”这个定语给省略掉，就留下一句“一切物体都以光速运行” ，留下读者在那里一脸懵逼。

本文图片

这个事情呢，说简单也简单，说麻烦也麻烦。但小编决定好好跟大家说道说道，让你享受知识带来的乐趣
当然，这个问题对我们深入理解狭义相对论，从牛顿力学的时空观转向相对论的时空观也大有好处。
你们觉得这个问题反常，是因为我们平常理解的速度都是建立在“空间”的概念上的。
什么是速度？速度就是位移除以时间。在单位时间内，我在3维空间里移动了多少，速度就是多少，这是我们的常规理解。
在这种理解下，每个物体的速度当然是可变的，可大可小，可快可慢。而且，我们还知道，在相对论里，任何有质量的物体，它的速度都不会超过光速。
所以，在这种语境下，我们就会觉得“一切物体的速度都是光速”非常反常，甚至非常扯淡了。即便他说了是在相对论里，你也搞不懂为什么相对论里会这样说。
要理解这句话，关键就在那个定语“在时空“里。当我们在说”一切物体的速度都是光速c“时，我们说的这个速度是指在时空中的速度，而不是我们一贯理解的在空间中的速度。
“空间”和“时空” ，一字之差，意思却天差地别。这一字之差，也是牛顿力学和相对论力学之间的关键差别。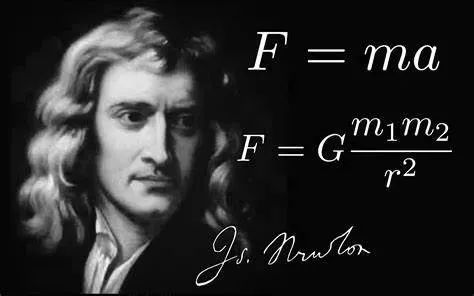

本文图片

狭义相对论的背景是4维闵氏时空，它最基本的东西是事件。一个事件包含3个空间坐标和1个时间坐标，时间和空间在相对论这里地位平等了。
我们之前理解的速度，都是定义在3维空间里的速度。一个物体从3维空间中的一个点（具有3个空间坐标）移动到另一个点，我们用这个位移除以时间得到的速度。
那么，到了相对论，最基本的东西是4维时空，而不再是3维空间。如果我们想要仿照上面的方法，在4维时空里定义速度，我们要怎么定义呢？
类似的，我们当然也希望，从4维时空的一个点移动到另一个点的“时空位移”除以某种时间，得到4维时空中的速度，对不对？
因此，要搞定4维时空里的速度，我们就需要先搞定4维时空中的“位移”和“时间” ，我们来分别看一看。
4维时空中的位移（以后就简称4维位移吧）好办，就是仿照3维空间里的坐标系，我们在3维空间坐标系里再加一个时间轴，组成了一个4维的坐标系，这样画的图就是时空图。
这样， 4维坐标系里的每一个点就有4个坐标，例如事件点p1（x1,y1,z1,t1)时空图里的每一个点就代表一个事件。同样，如果还有一个事件点p2(x2,y2,z2,t2) ，那么，我们把事件点p1从时空图里移动到事件点p2的位置移动定义为4维位移，这就非常合理了吧。
也就是说， 3维空间里的位移，就是我们从3维空间的一个点移动到另一个点（比如从家移动到学校）。那么， 4维时空里的位移，就是我们从4维时空的一个事件点移动到另一个事件点。
因为事件是有4个坐标的（3个空间坐标， 1个时间坐标），因此，如果我一直坐在家里没动。那么，从3维空间来看，我的坐标点没有变化（因为x,y,z都没变），但是，从4维时空来看，我7点在家这个事件点跟我8点在家这个事件点就是两个不同的时空点了。
7点在家的时候，你的时空点可能是（0,0,0,7）， 8点在家的时候就是（0,0,0,8）了。你的空间坐标没变，但是时间坐标变了，因此在4维时空图里，这依然是两个不同的点，因此它们之间依然有位移。懂了么？
也就是说，即便我一直呆在家里没动，从3维空间的角度来看，我确实没动（因为空间坐标没变），因此速度为0 。但是，从4维时空的角度来看，即便我一直坐在家里，我依然在运动（因为虽然空间坐标没变，但是时间坐标在变），因此速度不为0 。
这个4维时空下的速度，就是我们标题里说的4维速度，就是那个“一切物体都以光速运动”的速度。
相信看到这里，你应该有点感觉了。
【光速|听说一切物体在时空中的速度都是光速c？】如果你能理解我即便呆在家里没动，我依然有4维速度，那问题就解决了一半。因为剩下来的工作，无非就是证明这个速度就是光速c ，而且对所有物体都成立。
到了这里，我请大家闭上眼睛，想象自己在4维时空里遨游。想象你自己的每一个瞬间，每一个动作，都在4维时空里穿梭，你不仅在空间中穿梭，也在时间中穿梭，你时空里飞舞。

本文图片

因为时间长河永远向前奔涌，时间永远在向前流动。因此，即便你一动也不动，呆在那里傻坐着，你也被时间长河裹挟着飞速移动。
逝者如斯夫，不舍昼夜。
如果你不想在时间长河里傻坐着，你也想运动运动，学习刘翔、博尔特飞奔一波，开飞船去宇宙深处活动一下。于是，你的空间坐标就发生了改变，你就有了空间上的速度。
那么，空间上的这个速度会给你带来什么改变呢？
有一个但凡接触过相对论都知道的结论：钟慢效应。
也就是说，当你在空间上有了速度的时候，你的时间开始变慢，而且速度越快，时间减慢得越快。说得更通俗一点就是，当你在空间上有速度的时候，你在时间上的速度就会相应减慢，你在空间上的速度越快，你在时间里的速度就越慢。
就好像你骑着一匹赤兔马在时空里飞奔，由于赤兔马的最大耐力和速度是有限的。因此，当你向空间方向飞奔时，你在时间方向上的速度就慢了下来；当你朝时间方向上飞奔的时候，你在空间上的速度自然就慢了下来。
当你在空间里的速度达到最小，也就是静止不动时，赤兔马所有的体力都在时间方向上冲刺，这时候时间流逝得是最快的。当你空间里的速度接近最大（光速c) ，你在时间里的流逝几近停滞，这就是钟慢效应的极致。
而赤兔马在时空中的速度，就是光速c ，你可以按比例把它分配到时间和空间中，但是它们的“总和”保持不变。简单来说，这就是狭义相对论。
如果你以后习惯了在4维时空中思考问题，而不再一直死守3维空间，那你会觉得狭义相对论的一切东西都非常的简单自然。
相反，如果你一直试图死守在3维空间理解4维的相对论，那么，这就好像你试图通过盯着2维墙壁上的影子，来理解外面的3维世界一样。不是不可以，但是会非常非常的困难，属于纯粹给自己找不痛快。
因此，我们接下来要开始尝试在4维时空里重新理解相对论，理解相对论力学。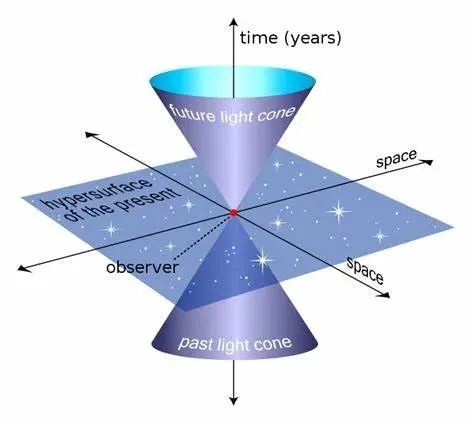

本文图片

我们要在4维时空里重新定义4维位移（两个时空点之间的位置变化），重新定义4维速度、4维加速度、4维力、4维动量……
站在这样的角度，我们才能用最自然的角度来欣赏相对论力学。在这样的角度里，我们标题说的“所有物体在时空里的速度（也就是4维速度）都是光速c”就会变得理所当然。
因为你只要把4维速度的形式写出来了，你就会发现任何4维速度的模的平方都是c2 ，所以就有标题的结论就不足为奇了。
最后，我再补充说明一点。
我在上面定义4维速度时，跟大家说了4维位移（4维时空图里两个事件点的位置移动），这个好理解。但是我一直没有说对应的时间是怎么定义的。
毕竟，速度速度嘛，位移除以时间才叫速度。
我们在牛顿力学，在3维空间里定义速度都比较简单，因为牛顿力学里有绝对时间，我们直接用3维空间点的位置移动（3维位移）除以绝对时间（就是我们过去理解的时间）就可以得到速度。
但是，相对论里时间是相对的，并没有绝对时间了。那么，我们在4维时空里，要用4维位移去除以哪个时间呢？因为时间是相对的，那么，除以哪个参考系的时间似乎都不太合适。
比如，我7点从家里出发， 8点到学校，你要用这两个事件点组成的4维位移除以哪个时间呢？家里的时间？学校的时间？路上的时间？
显然都不合适！
但是，有一个时间是比较特殊的，对我而言是唯一的，那就是：我自己随身携带的时钟指示的时间。
我从家里出门时往兜里放一块表，这块表一直跟我保持相对静止，它指示的时间自然与众不同。这种跟物体一直保持相对静止的时钟指示的时间，叫固有时。
我们的4维速度，就是用4维位移除以这个固有时。而在时空图里，这个固有时又刚好代表了世界线的长度，这就非常有意思了。
最后，一句话回答为什么说一切物体在时空中的速度都是光速c？
答：因为一切物体的4维速度的模的平方刚好等于光速c的平方。
来源：长尾科技

编辑：jita

光速|听说一切物体在时空中的速度都是光速c？

推荐阅读

山河令女主是谁周也的个人简介

地砖不喜欢怎么改装

龙盛2号西瓜有何特点

对于学生来说，补课到底有没有用？

冒险王2魔星任务位置冒险王2介绍

好用的睫毛夹排行榜睫毛夹什么牌子的好用

吉野家的日式小火锅咋样有吃过的吗

景龙红薯粉丝是哪儿的特产吗？景龙红薯粉丝介绍

一键刷机软件有什么啊

win10声音无法找到输入设备

邯郸有什么值得去玩的地方呢

暖暖巧克力咖啡的做法（时尚饮品）

赤豆的营养价值有那些

金针菇的做法大全有哪些

以梦为马不负韶华下句

什么衬衫搭配休闲牛仔裤牛仔裤和什么衣服搭配

大承气汤加减治原发性肝癌并发肝性脑病医案、配方

隔夜普洱茶还能喝吗

微信怎么添加滴滴出行

win10摄像头灯亮却不能用电脑如何打开摄像头