易坊好文馆

  1. 首页 > 玩科技 >

正态分布|正态分布的前世今生（3）

极限 漏洞 中心 条件 高尔顿 李雅 统计学 拉普拉斯 定理 正态 正态分布 概率论 普诺夫 凯特勒

更多正态分布的介绍 ， 参见
正态分布的前世今生（1）
正态分布的前世今生（2）
>>>>
六、开疆扩土 ， 正态分布的进一步发展
19世纪初 ， 随着拉普拉斯中心极限定理的建立与高斯正态误差理论的问世 ， 正态分布开始崭露头角 ， 逐步在近代概率论和数理统计学中大放异彩 。 在概率论中 ， 由于拉普拉斯的推动 ， 中心极限定理发展成为现代概率论的一块基石 。 而在数理统计学中 ， 在高斯的大力提倡之下 ， 正态分布开始逐步畅行于天下 。
6.1 论剑中心极限定理

正态分布|正态分布的前世今生（3）
文章图片

在这个问题的处理上 ， 拉普拉斯充分展示了其深厚的数学分析功底和高超的概率计算技巧 ， 他首次引入了特征函数(也就是对概率密度函数做傅立叶变换)来处理概率分布的神妙方法 ， 而这一方法经过几代概率学家的发展 ， 在现代概率论里面占有极其重要的位置 。 基于这一分析方法 ， 拉普拉斯通过近似计算 ， 在他的1812年的名著《概率分析理论》中给出了中心极限定理的一般描述：

正态分布|正态分布的前世今生（3）
文章图片

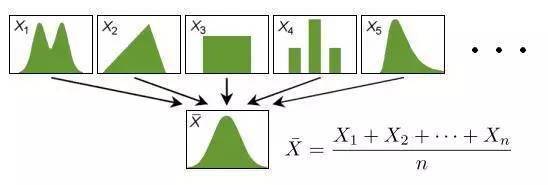
多么奇妙的性质 ， 随意的一个概率分布中生成的随机变量 ， 在序列和(或者等价的求算术平均)的操作之下 ， 表现出如此一致的行为 ， 统一的规约到正态分布 。

正态分布|正态分布的前世今生（3）
文章图片

概率学家们进一步的研究结果更加令人惊讶 ， 序列求和最终要导出正态分布的条件并不需要这么苛刻 ， 即便X1,?,Xn并不独立 ， 也不具有相同的概率分布形式 ， 很多时候他们求和的最终归宿仍然是正态分布 。 一切的纷繁芜杂都在神秘的正态曲线下被消解 ， 这不禁令人浮想联翩 。 中心极限定理恐怕是概率论中最具有宗教神秘色彩的定理 ， 如果有一位牧师拿着一本圣经向我证明上帝的存在 ， 我是丝毫不会买账；可是如果他向我展示中心极限定理并且声称那是神迹 ， 我可能会有点犹豫 ， 从而乐意倾听他的布道 。 如果我能坐着时光机穿越到一个原始部落中 ， 我也一定会带上中心极限定理 ， 并劝说部落的酋长把正态分布作为他们的图腾 。
中心极限定理虽然表述形式简洁 ， 但是严格证明它却非常困难 。 中心极限定理就像一张大蜘蛛网 ， 棣莫弗和拉普拉斯编织了它的雏形 ， 可是这张网上漏洞太多 ， 一个多世纪来 ， 数学家们就像蜘蛛一样前赴后继 ， 努力想把所有的漏洞都补上 。 在十九世纪 ， 珀松(Poission)、狄利克莱(Dirichlet)、柯西(Cauchy)、贝塞尔(Bessel)这些大蜘蛛都曾经试图对把这张网上的漏洞补上 。 从现代概率论来看角度 ， 整个十九世纪的经典概率理论并没有能输出一个一般意义下严格的证明 。 而真正把漏洞补上的是来自俄罗斯的几位蜘蛛侠：切比雪夫(Chebyshev)、马尔可夫(Markov)和李雅普诺夫(Lyapunov) 。 俄罗斯是一个具有优秀的数学传统的民族 ， 产生过几位顶尖的的数学家 ， 在现代概率论的发展中 ， 俄罗斯的圣彼得堡学派可以算是顶了半边天 。 把漏洞补上的严格方案的雏形是从切比雪夫1887年的工作开始的 ， 不过切比雪夫的证明存在一些漏洞 。 马尔可夫和李雅普诺夫都是切比雪夫的学生 ， 马尔科夫沿着老师的基于矩法的思路在蜘蛛网上辛勤编织 ， 但洞还是补得不够严实；李雅普诺夫不像马尔可夫那样深受老师的影响 ， 他沿着拉普拉斯当年提出的基于特征函数的思路 ， 于1901年给出了一个补洞的方法 ， 切比雪夫对这个方法大加赞赏 ， 李雅普诺夫的证明被认为是第一个在一般条件下的严格证明；而马尔科夫也不甘示弱 ， 在1913年基于矩法也把洞给补严实了 。

推荐阅读


上一篇：状态|贝叶斯网络

下一篇：民航|翔宇航校 | 青春、梦想、初心，飞行学员“飞”常了不起！