质数是那些只能被自身和1整除的整数,比如前七个质数是2,3,5,7,11,13,17 。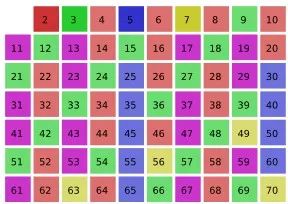
图示为埃拉托色尼筛选法 , 可以用于寻找质数 。 图源 SKopp, CC BY-SA 3.0.每一个正整数都可以借助一种特定的数学结构写成质数的乘积 , 例如 30 = 2×3×5。 质数就像是构成其他整数的基本积木 , 而这就是人们觉得它们有趣的原因 。 质数是无穷多的 , 而这一点早已被古希腊数学家熟知 , 无论你在数轴上移动多远总有一个质数在你前面 。 下面是希腊最著名的数学家欧几里得的证明 。 假设质数是有限的 。 我们可以用 p1 , p2 , p3 等来表示 , 直到最后一个质数 pn。 现在定义某个数字 P :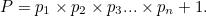
比方说如果只有5个质数:p1 = 2, p2 = 3, p3 = 5, p4 = 7, p5 = 11 , 那么存在一个数 P :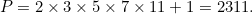
如果 P 本身是质数(就像在我们的例子中一样) , 那么很明显它不可能是我们列表中的一个质数:因为它比所有的质数都大 。 如果 P 不是质数 , 那么 , 就像其他自然数一样 , 它一定可以写成质数的乘积 。 我们选一个能被 P 整除的质数 , 用 p 表示 。 可以看出 ,p 不能是 p1 到 pn 的任何质数 , 否则就会出现余数 1 :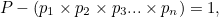
而 1 不能被任何其他的自然数整除 。 因此 , 集合 p1,p2,p3…pn 并不能包含我们假设的所有质数 。 这个矛盾意味着质数一定是无限多的 。 几千年来 , 我们一直知道有无限多个质数(参见这里的证明) , 但并没有一个简单的公式告诉我们它们都是多少 。 强大的计算机算法使我们能够找到越来越大的质数 , 但却永远不可能把它们全部写下来 。 质数定理告诉我们质数在其他整数中的分布 。 它试图回答这样一个问题:“给定一个正整数 n, 包括 n 在内的所有整数 , 有多少个是质数?”质数定理并没有精确地回答这个问题 , 而是给出了一个近似值 。 宽泛地说 , 对于比较大的整数 , 表达式: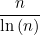
是一个很准确的质数估计 , 而且随着n的增大 , 这个估计也会变得更准确 。 其中 ln(n) 是自然对数 , 可以通过计算器得到 。 举个例子 , 让我们来看看 n=1000 的情况 。 此时所有质数可以在这个列表中查找 。 我们的估计是: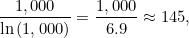
推荐阅读
- 核心|中科大陈秀雄团队成功证明凯勒几何两大核心猜想,研究登上《美国数学会杂志》
- 社会|机器的猜想与边界
- 形式|法国学者29页预印本论文「证明」黎曼猜想,这次的方向对了吗?
- IT|有史以来最强大的奥迪A8下线 剑指迈巴赫S级
- 核心|中国团队成功证明数学界两大核心猜想
- 会|悬而未决60年 我科学家证明凯勒几何两大核心猜想
- 稳定性|重磅!中科大团队成功证明了两个数学界核心猜想……
- 稳定性|中国团队成功证明两个国际数学界60多年悬而未决的猜想
- 测地|中国科大陈秀雄团队成功证明凯勒几何两大核心猜想
- 新浪科技综合|中国科大陈秀雄团队成功证明凯勒几何两大核心猜想






