马赛|拓端数据tecdat:R语言 PCA(主成分分析)，CA(对应分析)夫妻职业马赛克图可视化_职业|plot|变量|矩阵|差异|夫妻

原文链接：http://tecdat.cn/?p=22762
原文出处：拓端数据部落公众号
主成分分析法是数据挖掘中常用的一种降维算法,是Pearson在1901年提出的,再后来由hotelling在1933年加以发展提出的一种多变量的统计方法，其最主要的用途在于“降维” ，通过析取主成分显出的最大的个别差异,也可以用来削减回归分析和聚类分析中变量的数目，与因子分析类似。
所谓降维，就是把具有相关性的变量数目减少，用较少的变量来取代原先变量。如果原始变量互相正交，即没有相关性，则主成分分析没有效果。
对应分析（CA）是适用于分析由两个定性变量（或分类数据）形成的大型应变表的主成分分析的扩展。本文通过析取主成分来分析夫妻职业的个别差异。
夫妻职业数据考虑以下数据，对应于一对夫妻中的职业。我们有以下的频数表
read.table(data.csv",header=TRUE)

文章图片

传统上，对于这种数据，我们习惯于使用卡方检验，卡方距离，以及卡方贡献来查看数据的差异性
chisq.test(M)

文章图片

马赛克图 Mosaic plot常常用来展示Categorical data(分类数据)(关于不同的数据类别， mosaic plot 强大的地方在于它能够很好的展示出2个或者多个分类型变量(categorical variable)的关系. 它也可以定义为用图像的方式展示分类型数据。
当变量是类别变量时，且数目多于三个的时候，可使用马赛克图。马赛克图中，嵌套矩阵面积正比于单元格频率，其中该频率即多维列联表中的频率。颜色和阴影可表示拟合模型的残差值。
我们可以将其结果用马赛克图来形象化。
plot(tM)
丈夫在行中，妻子在列中。重要的联系是蓝色或红色，这两种颜色分别对应于 "正 "联系（比独立情况下的联合概率高）或 "负 "联系（比独立情况下的联合概率低）。

文章图片

在另一个方向
plot(M)
但结论与之前一样：对角线上有很强的蓝色数值。

文章图片

换句话说，这些夫妻在职业方面是相对相似和单一的。
主成分分析和对应分析在对应分析中，我们查看概率表，在行或列中。例如，我们可以定义行，它是概率向量

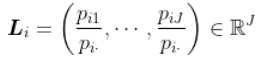
文章图片

N/apply(N,1,sum)
注意到，我们可以写出

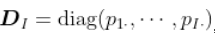
文章图片

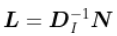
文章图片

我们的线向量的重心在这里

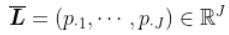
文章图片

同样，注意到 , 我们可以用矩阵的方式来写, .

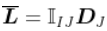
文章图片

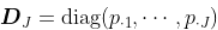
文章图片

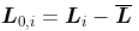
文章图片

L0=(t(L)-Lbar)
对于每一个点，我们都将（相对）频率作为权重进行关联，这相当于使用矩阵。为了测量两点之间的距离，我们将通过概率的倒数对欧氏距离进行加权，。两条线之间的距离是

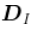
文章图片

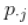
文章图片

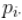
文章图片

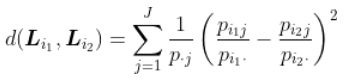
文章图片

然后我们将用这些不同的权重做主成分分析。从矩阵的角度来看

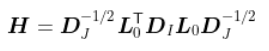
文章图片

我们注意到特征向量，我们定义了主成分

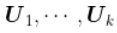
文章图片

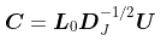
文章图片

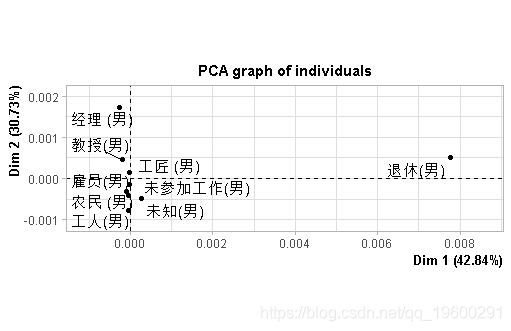
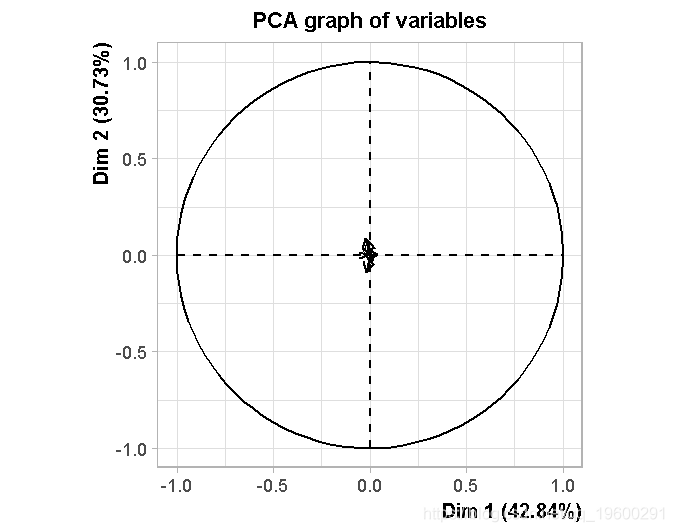
对线条的前两个成分的投影，在此给出了
PCA(L0,scal=FALSE

文章图片

文章图片

我们的想法是将对应于行的个体进行可视化。在第二步中，我们做相同的事情，在列中

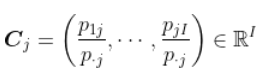
文章图片

N/apply(N,2,sum))
中心：

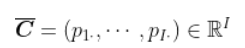
文章图片

C0=C-Cbar
主成分分析然后我们可以做一个主成分分析
PCA(matC0
看个人的可视化。

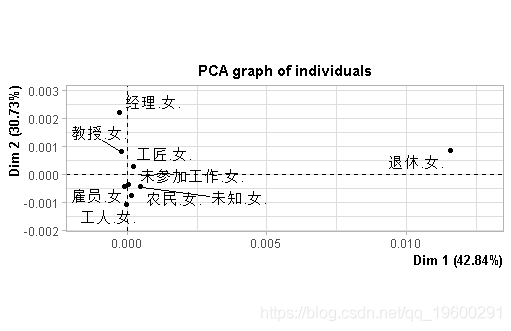
文章图片

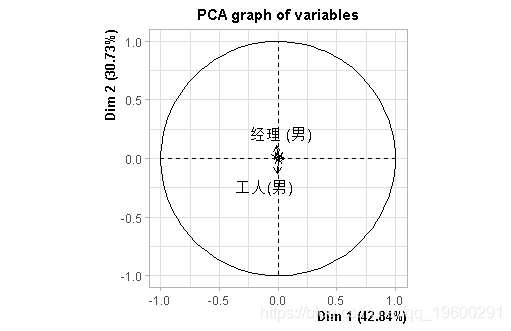
文章图片

对应分析对应分析的奇妙之处在于，我们 "可以 "在同一平面上表示个人的两个投影。

> plot(C[,1:2])

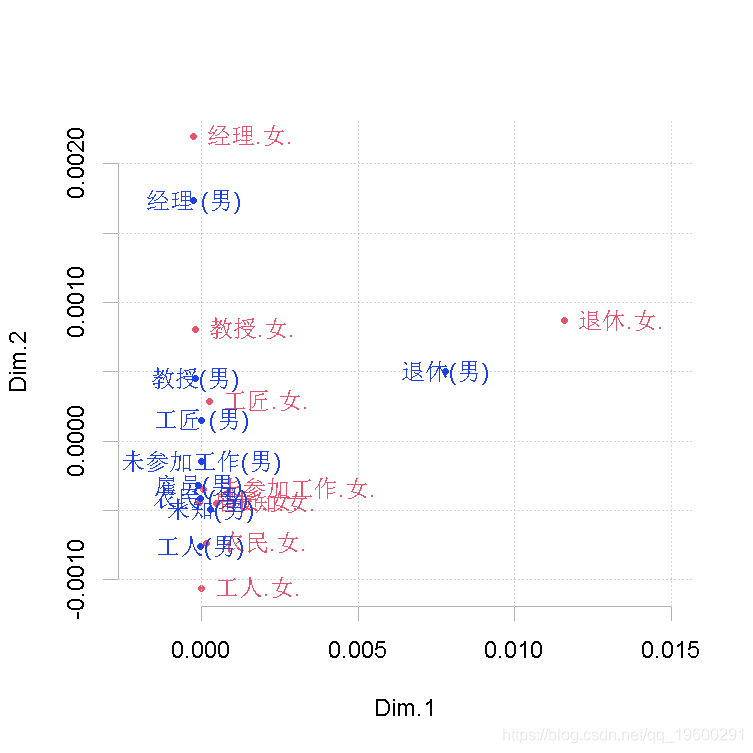
马赛|拓端数据tecdat:R语言 PCA(主成分分析)，CA(对应分析)夫妻职业马赛克图可视化

文章图片

结果如下
> afc=CA(N)

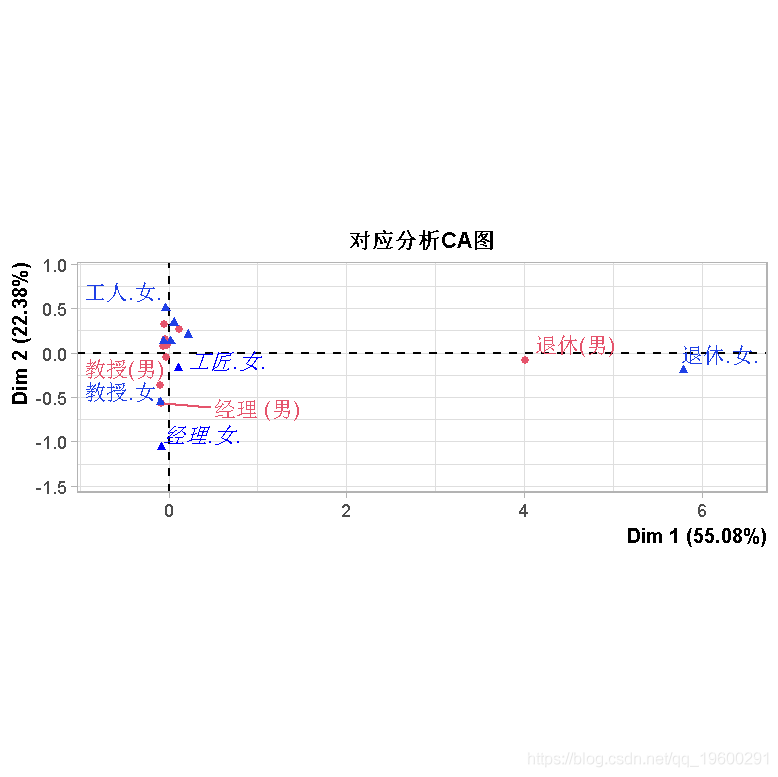
文章图片

文章图片

最受欢迎的见解
1.matlab偏最小二乘回归(PLSR)和主成分回归(PCR)
2.R语言高维数据的主成分pca、 t-SNE算法降维与可视化分析
3.主成分分析(PCA)基本原理及分析实例
4.基于R语言实现LASSO回归分析
5.使用LASSO回归预测股票收益数据分析
6.r语言中对lasso回归， ridge岭回归和elastic-net模型
7.r语言中的偏最小二乘回归pls-da数据分析
8.r语言中的偏最小二乘pls回归算法
【马赛|拓端数据tecdat:R语言 PCA(主成分分析)，CA(对应分析)夫妻职业马赛克图可视化】9.R语言线性判别分析（LDA），二次判别分析（QDA）和正则判别分析（RDA）