科普|你们说的这个实验结论，它可靠吗？_科技

本文图片

本文图片

在科学或医学领域，几乎每一个重大的新发现的背后，都藏着这样一个问题：是什么让我们确信结果足够可靠？从技术上来说，答案与统计显著性有关，但事实上，它也与判断标准在某种特定情况下是否合理有关。
在谈论统计显著性时，通常使用的是标准差，以小写希腊字母σ表示。这个术语讨论的是一个给定数据集中变化性的大小，换句话说，它反映了数据点是都聚集在一起的，还是非常分散的。
在许多情况下，实验的结果会遵循正态分布。例如，如果你把一枚硬币掷100次，然后数一数正面出现多少次，会发现平均来说答案应该是50次。但是，假设你真的进行了1000组这样的“百次掷硬币”测试，在大多数情况下，每组测试中可能会出现50次左右的正面，但不一定是正好50次。可能有差不多的组掷出了49次正面和51次正面的情况，或许还有不少组掷出了45次或55次正面的情况，但可能很少出现只有10次正面或者多达90次正面的情况。
这1000组测试结果可以构成一个你可能非常熟悉的形状——它中间最高，越往两边越来越矮，这条曲线也被称为钟形曲线。这就是正态分布。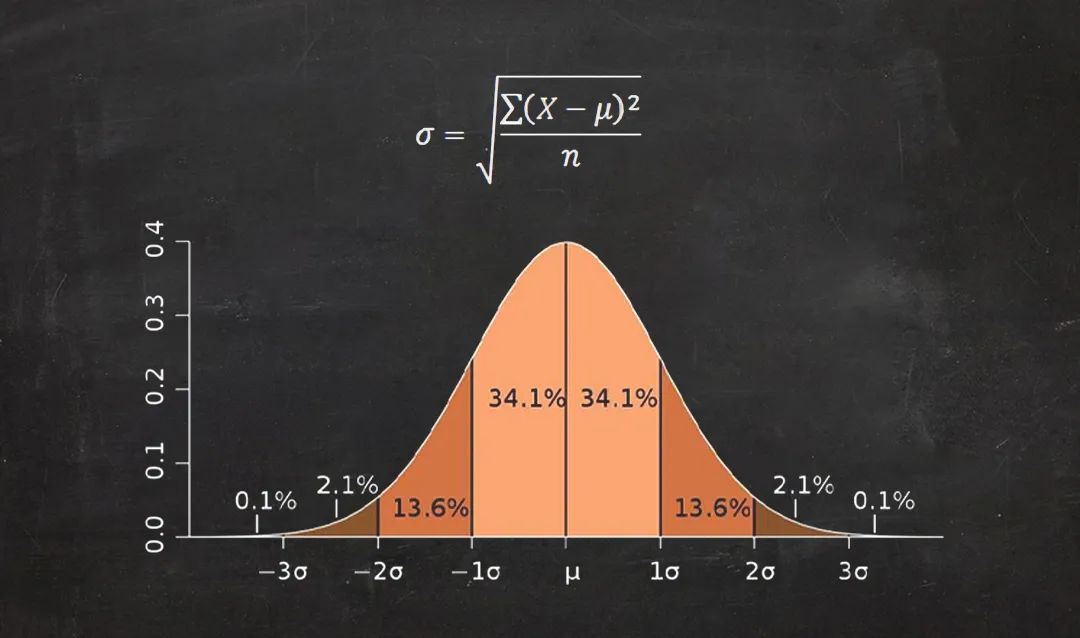

本文图片

差（deviation）是给定数据点与均值（μ）的距离。在上面的掷硬币例子中，掷出47次正面与均值50次之间的差就是3 。在计算上，标准差σ就是所有差的平方的平均数的平方根。在距离正态分布曲线的均值一个标准差（±1σ）的位置画出一片区域，就能定义一个包含约68%的数据点的范围；如果扩大至两个标准差（±2σ），则将包含约95%的数据点；如果是三个标准差（±3σ），则将范围扩大到了约99.7% 。

本文图片

什么时候某个特定的数据点（也就是研究结果）能被认为是显著的呢？标准差可以提供一种标准：如果一个数据点与被测试的模型有数个标准差之远，这就是一种有力的证据，证明这一数据点与该模型不一致。然而，要如何运用这种标准则要视情况而定。
麻省理工学院John Tsitsiklis教授说：“统计学是一门艺术，有很大的创造空间，也有很大的错误空间。 ”这门艺术的关键之一，就是决定对于给定的条件，什么样的测量方法是有意义的。
例如，如果你要对人们将计划如何在选举中投票一事进行民意调查，公认的惯例是，高于或低于均值的两个标准差（95%置信水平）是合理的。这意味着，如果你向所有人调查了一个问题并得到了一个确定的答案，然后向随机抽样的1000人询问同样的问题，那么有95%的可能，第二组的结果会落在距第一次结果2σ的范围内。
但反过来说，这也意味着有5%的情况，结果会超出2σ的范围。这样的不确定性对民调来说是可以接受的，但对于一项关键的实验结果来说，尤其是那种挑战了科学家对一个重要现象的理解的结果，情况可能又不一样。
2011年秋天，欧洲核子研究中心（CERN）的一项实验宣布，可能探测到了中微子的运动速度超过光速的现象。从技术上讲，这个实验的结果有着极高的置信水平——6σ 。在大多数情况下， 5σ已经被认为是显著性的黄金标准，那相当于这一发现是随机变化的结果的概率，只有百万分之一；而6σ则基本上在说，只有五亿分之一的概率，这一发现是随机的侥幸结果。
但是，这项实验结果意味着，一个世纪以来被广泛接受的物理学，且已经在之前的数千种不同实验中得到证实的物理学，将有可能被推翻。对这样一项具有如此颠覆性的实验来说， 6σ的结果还远远不够好。并且，要接受这一结果的一个大前提是假设研究人员已经正确地进行了分析，且没有忽略系统性的错误来源。事实证明，正如大多数物理学家所认为的，正是一些被忽视的错误来源，才导致出现了如此出乎意料的“革命性”结果。
同样在2011年， CERN还宣布了另一项可能的探测结果，被称为希格斯玻色子。这是一种理论预测的亚原子粒子，它能帮助解释粒子为什么有质量。虽然当时的探测结果只有2.3σ的置信水平看，但是这一结果符合基于当前物理学的预期，尽管在统计上的置信水平要低得多，但大多数物理学家从一开始就对它很有信心。

本文图片

在其他一些领域，情况可能更为复杂。不少人认为，统计学真正棘手的地方是社会科学和医学。例如， 2005年，一篇题为《为什么大多数发表的研究结果都是错误的》论文指出，如果能够以足够多的方式去研究大型数据集，就能很容易地找到符合统计显著性的通常标准的例子，即便它们实际上只是随机变化。如果一台计算机浏览了数百万种可能性，即使结果看似达到了5σ的显著性水平，一些满足标准的随机模式仍然可能被发现。
当这种情况发生时，研究人员不会发表那些没有通过显著性检验的结果，而是选择发表一些随机相关性，这样反而会让人觉得是收获了真实的发现。所以最终发表的其实只是侥幸。
其中一个例子是，过去十数年发表的许多论文都声称，某些行为或思维过程与磁共振成像（MRI）捕捉到的大脑图像之间存在着显著的相关性。但有的时候，这些测试发现的显著相关性，其实只是系统中自然波动的结果，也就是噪声。 2009年，一位研究人员“重复”了其中一个关于面部表情识别的实验——他扫描了一条死鱼，并发现了“显著”的结果。
Tsitsiklis说：“如果你在足够多的地方寻找，你就会得到这样一个‘死鱼’的结果。 ”相反在许多情况下，统计显著性较低的结果仍有可能“告诉你一些值得研究的事情” 。
符合公认的“显著性”定义，并不一定就意味着它就是“显著”的，这完全取决于整个故事的背景。
参考来源：
https://news.mit.edu/2012/explained-sigma-0209
来源：原理
【科普|你们说的这个实验结论，它可靠吗？】编辑：dogcraft

科普|你们说的这个实验结论，它可靠吗？

推荐阅读

流行语录

the 美媒：推特账号被封，特朗普的离任“静悄悄”

腿抽筋该怎么办孕妇腿抽筋是怎么回事

华融湘江银行信用卡额度高吗

牙齿松动了怎么办？导致牙齿松动的原因有哪些？

献血到底有啥好处和禁忌答案都在这里

孩子能喝罗汉果水吗

白鹭有哪些种类

搪瓷锅能用煤气灶吗

女生闷骚勾魂网名2字陌颜

月经期到底能喝醪糟吗

彤仕的寓意

首次发现可燃冰在哪

100句非主流发在QQ空间上的爱情说说

全自动手表是什么原理

很有哲理的网名

鹧鸪的功效有哪些哪些人吃最好

变叶木的养殖方法和注意事项

关于描述雪的优美句子关于描述雪的优美句子有哪些

征信报告是黑名单是不是不能坐高铁了??? 你知道吗