易坊好文馆

  1. 首页 > 生活百科 >

物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法( 二 )

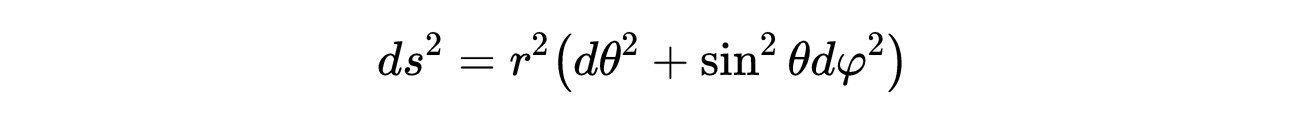
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图

  • 式9：Kruskal图中每个点的几何形状，这是一个二维球体。
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
  • 图7：Kruskal图。这四个象限是黑洞内部(II)，白洞内部(II’)和两个外部区域(I和I’)
爱因斯坦-罗森桥让我们考虑超曲面t ' =0（回想一下，Kruskal图中的每个点都是一个二维球体）。这个超曲面（如式6和式8所示）上的线元素为：
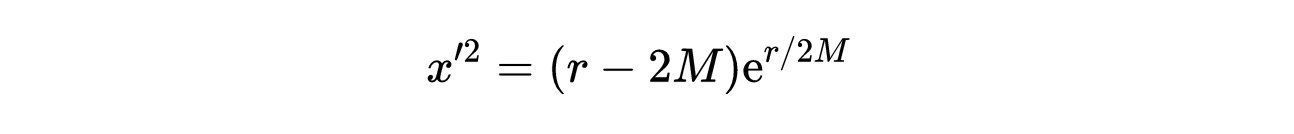
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
  • 式10：t ' =0时，式6和式8中给出的超曲面的线元素。
r的第二个方程解为：
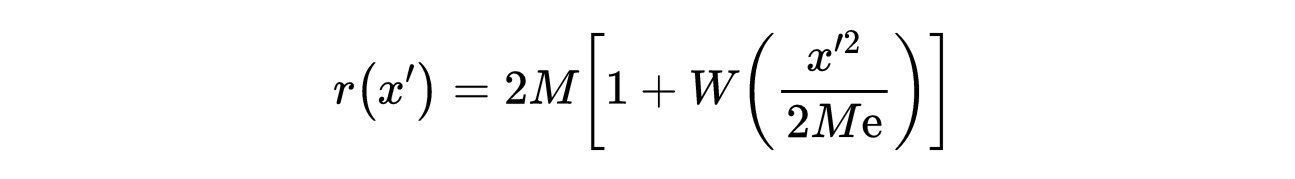
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
  • 式11：式10中第二个方程的解。
其中W是朗伯函数。当x '从正无穷到负无穷时，上述函数减小到最小半径r = 2M，出现在x ' =0处。
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
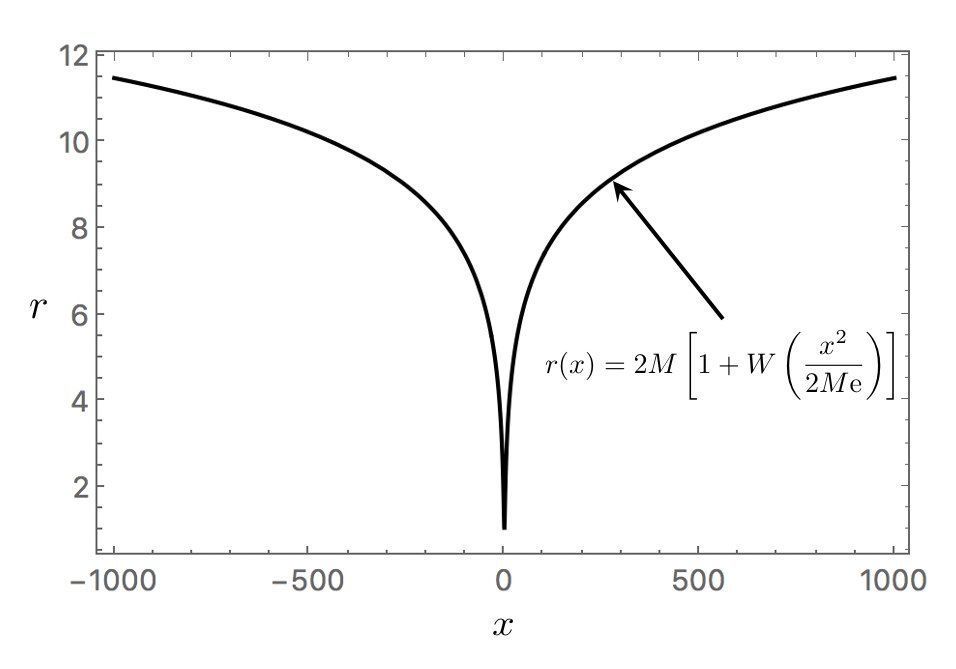
  • 图8：设2M=1时式11的曲线图。
既然图中的每个点都是二维球面，我们可以选择一个截面θ = π/2。如图5所示，这个横截面就是赤道面。这个指标简化为:
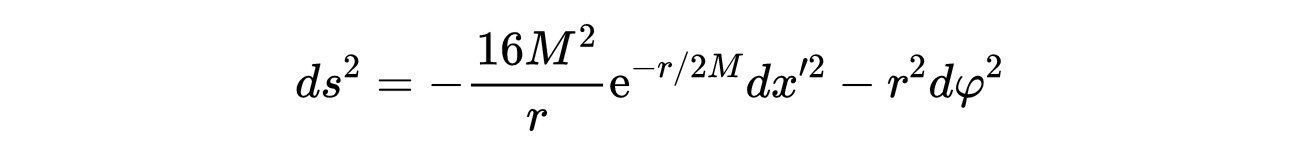
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
  • 式12：θ = π/2的式10中的度规。
我们可以通过以下方式更好地理解这个度规。考虑一个嵌入三维平面空间的线元方程12的二维曲面。它看起来如下图所示。
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
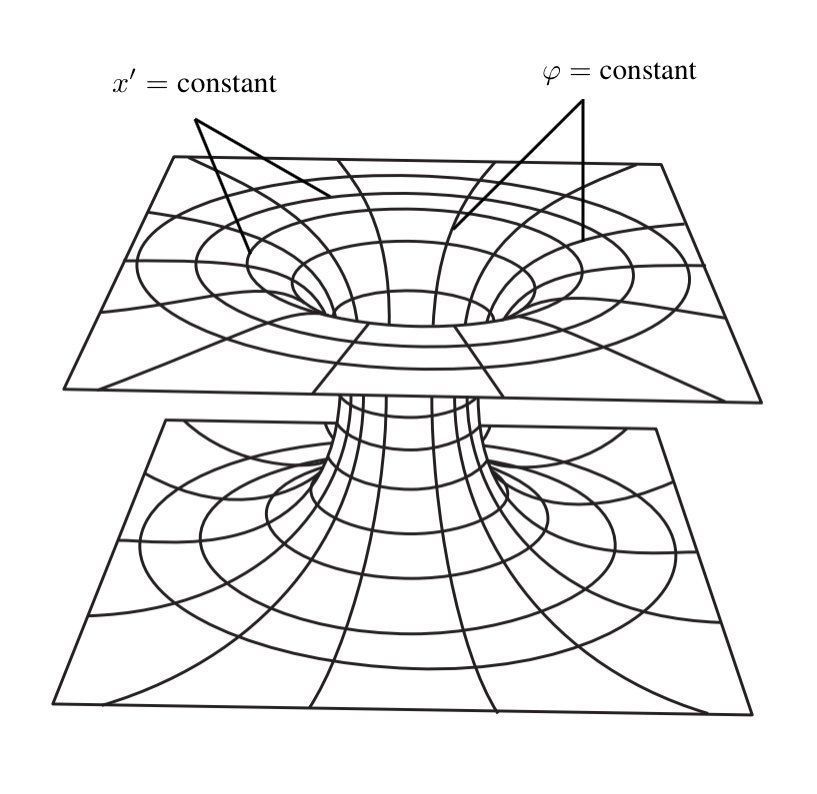
  • 图9：嵌在三维平面空间中的线元由式12给出的二维曲面。
正如前面提到的，当t ' =0保持不变并沿x '移动时，我们发现在x ' =0点对应的球面半径是最小的（r=2M）。这是连接两个宇宙的史瓦西流形的“咽喉”。这个解不限于t ' =0。随着我们改变“喉道”的半径，直到它闭合，将两个宇宙彼此隔开（图10）。这个度规描述了爱因斯坦-罗森桥或史瓦西虫洞。
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
  • 图10
与Kruskal图相对应的解被认为是一个极大扩展的解，与一个典型的黑洞的解是不同的，这是一个恒星坍塌的结果。后者的图既不包含白洞，也不包含对应于另一个宇宙的区域。这个新宇宙在最大扩展解中的真实存在仍然是一个悬而未决的问题。
广义相对论的爱因斯坦场方程是局部的。这意味着它们不能决定时空的整体几何性质。解方程10可以嵌入不同拓扑的时空中。下面图11中的例子显示了一个连接两个遥远时空区域的史瓦西虫洞。
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
  • 图11：连接两个遥远时空区域的史瓦西虫洞
不幸的是，1962年，两位美国物理学家约翰·惠勒和罗伯特·富勒证明，如果施瓦茨子虫洞将同一宇宙的两个部分连接起来，它们会迅速地将任何粒子（包括光子）夹在这两个区域之间（这种虫洞是不稳定的）。
这种不稳定性是由于两个特性造成的：
  1. 史瓦西虫洞是有时间依赖性的。虫洞的打开和关闭速度太快，旅行者无法通过。
  2. 虫洞咽喉处的潮汐力太强，会杀死旅行者。
其他类型的虫洞【 物理学|虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法】因此，爱因斯坦-罗森桥是不能被穿越的。然而，如果它们的“喉咙”能在外来物质（负质量的物质）存在时保持打开，那么稳定性是可能的。
可穿越虫洞
以下是一个可穿越虫洞应该遵循的几个条件：
  1. 虫洞度规应该是静态的（与爱因斯坦-罗森桥相反），并遵循广义相对论场方程
  2. 球对称（这将使数学处理更简单）
  3. 在连接两个渐近平坦的时空区域的解中一定有一个“喉道”
  4. 旅行者在穿过虫洞时所感受到的潮汐力必须足够小
现在让我们根据1988年美国理论物理学家基普·索恩（Kip Thorne）和迈克尔·莫里斯（Michael Morris）的一篇论文，用数学术语来研究一个可穿越的虫洞。
一个具有上述属性的虫洞的简单例子，用史瓦西坐标表示，具有以下线元素：
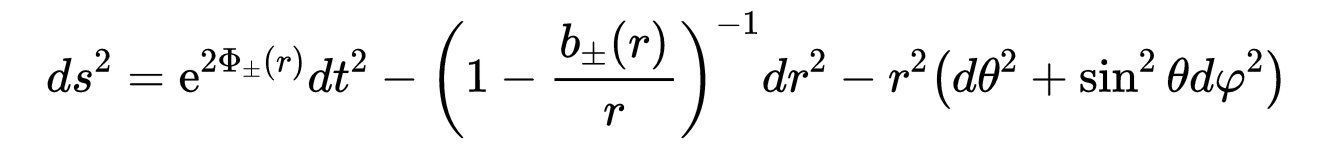
物理学 虫洞物理学——时空隧道的物理和数学特性，穿越时空的实现方法
文章插图
  • 式13
所谓的形状函数b(r)决定了虫洞的空间形状。喉道的周长由2πr给出。函数Φ称为红移函数。注意这个度规是与时间无关的。利用爱因斯坦场方程可以计算出虫洞咽道的张力。如果喉道的半径是3千米，喉道的张力等于质量最大的中子星中心的压强！

推荐阅读


上一篇：仰望天空 美图来袭！26日晚的“红月亮”你看见了吗？

下一篇：人民网 多图预警！“超级月亮+月全食”组团现身