噪声|墨子量子奖解读：引力波与量子精密测量_激光|位置|物理|涨落|墨子|引力

昨天（2020年12月10日）， “墨子量子奖”通过网络会议形式宣布。继前两届分别授予量子计算和量子通信领域之后， 2020年度“墨子量子奖”授予了量子精密测量领域。
“墨子沙龙”邀请施郁教授对获奖人的相关工作进行了解读。
作者 | 施郁（复旦大学物理学系教授）
2020年度“墨子量子奖”授予量子精密测量领域，获奖科学家是做出理论贡献的卡尔顿·凯夫斯（CarltonCaves）以及做出实验贡献的香取秀俊（Hidetoshi Katori）和叶军。评审委员会给出的信息如下[1] 。
CarltonCaves ，美国新墨西哥大学。获奖理由：凭借其在量子精密测量及量子信息理论方面的基础性工作，尤其是阐明干涉仪中的基本噪声及其在压缩状态下的抑制作用方面的工作；
Hidetoshi Katori ，日本东京大学；JunYe ，美国科罗拉多大学博尔德分校。获奖理由：凭借他们在量子精密测量方面的突破性成就，特别是在开发极其稳定和精确的光学原子钟方面的成就。
本文按照作者理解，评介获奖科学贡献以及相关研究领域。
1.用压缩光探测引力波
这是引力波探测中的量子噪声问题。对用来探测引力波的激光干涉仪， CarltonCaves分析了海森堡不确定关系所带来的测量精度极限，并且提出了用压缩光来克服这个极限。这个方法已经被探测引力波的激光干涉仪实际采用，而且最近已经发挥了作用。
引力波经过的地方，空间尺度发生振动变化，所以存在于其中的世间万物的长度都发生振动。这也就提供了引力波探测的途径。
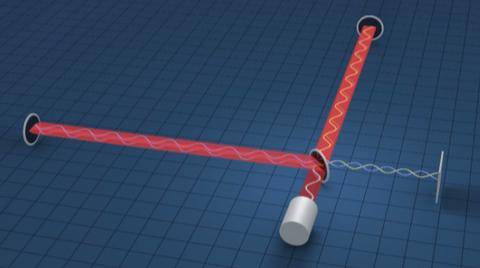
现在人们用激光干涉仪探测引力波。干涉仪通过激光的干涉效应，测量两臂的长度差（图1）。事实上，在每个臂上，激光都要来回反射多次，拉长有效路程。引力波通过时，会引起两臂长度差随时间振动，成为引力波的信号。

文章图片

图1. 引力波探测仪中的激光干涉（图源：T. Pyle/LIGO）
但是引力波引起的长度变化非常小，相对原来的长度只有大概10-22 。很多噪声都可能引起物体更大的长度变化，因此引力波探测的一个关键是要排除各种各样的噪声。
对于探测引力波的激光干涉仪来说，噪声包括低频率的辐射压强在镜子上引起的反冲、镜子悬挂系统的热噪声，以及高频率的量子噪声。之所以有量子噪声，是因为对于这么小的尺度，量子效应要起作用[2] 。
因此引力波探测不仅是引力物理问题，而且首先是精密测量问题，作为最精密的测量，与量子计量学密切相关。在量子计量学的历史上，引力波探测扮演了重要角色。
对于量子系统来说，一个物理量可能没有准确的值，称作有“量子涨落”或者“量子噪声” 。这限制了测量的准确性。而海森堡不确定关系给出了量子噪声下限。
对于同一个量子态而言，如果准确确定某个物理量（比如位置），那么与之不相容的物理量（比如动量，即质量乘以速度）就不能准确确定。一般来说，对于测量之前的量子态，被测物理量不是确定的，而测量这个物理量，总是使这个物理量变为一个确定值。但是，具体是哪个确定值，却是随机确定的。所以测量改变了测量时刻的量子态，然后量子态随时间演化。这又带来下一次测量的误差。
引力波探测的历史上，最初被考虑的设备是Joseph Weber的巨大金属棒。苏联的VladimirBraginsky首先研究了不确定关系对位置测量精度的限制。不确定关系说，位置的不确定乘以动量的不确定性不小于一个下限。如果在某个时刻准确确定了位置，那么该时刻的动量就不确定。但是，未来时刻的位置由测量时确定的位置、不确定的动量、时间共同决定，所以未来的位置就有了不确定性，它有一个非零、依赖于时间的最小值，叫做“标准量子极限” 。
Braginsky指出，通过所谓量子非破坏性测量，可以绕过标准量子极限。 1980年， Braginsky研究组、KipThorne及其合作者（包括他的学生Caves）两组团队独立提出了具体方案，叫做“频闪测量法” 。对于周期性的振动，每过一个周期，测量一次位置，这样虽然每次测量都改变了量子态，但是并不改变在这些时间的位置[3] 。
当时人们也研究用激光干涉仪探测引力波。 1980年，作为加州理工学院的博士生， Caves指出，干涉仪的主要误差并不是来自干涉仪中镜子的位置与动量的不相容，而是来自光场的光子数目的涨落，这叫做“散粒噪声”（shotnoise）[4] 。这是探测高频引力波的主要噪声。
爱因斯坦1905年就告诉我们，光由一颗一颗的光量子（后来简称“光子”）组成。作为一个物理量，光子数目可能不确定。不确定关系在这里表现为，光子数目的涨落（也就是不确定性）和辐射压强的涨落的乘积不小于一个下限。辐射压强的涨落正比于碰撞镜子的光子束流的涨落。这些涨落都是电磁场的固有性质。
可以有这样的光，其中光子数目的涨落很小，但是辐射压强的涨落很大，因此仍然满足不确定关系。这样的光叫做“压缩光” ，因为某个物理量（比如光子数目）的涨落得到了“压缩” 。压缩光可以通过非线性光学过程得到。
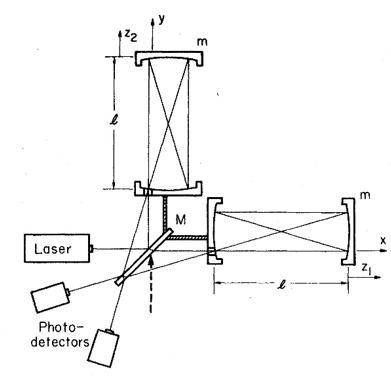
1981年， Caves建议，除了激光，再从干涉仪的另一个输入口注入压缩光（图2）[5] 。压缩光缩小了激光的不同光子到达光子探测器的时间差别。

文章图片

图2. 激光从左侧进入干涉仪，压缩光（图中用虚线代表）从下方进入 [5]
【噪声|墨子量子奖解读：引力波与量子精密测量】使用压缩光，降低散粒噪声，特别有利于探测来自中子星或小黑洞并合的引力波。这是因为，在并合过程中，中子星或者小黑洞互相绕行更快，因此发出的引力波的频率较高。
目前国际上测量引力波的干涉仪主要有：美国LIGO的两个直线相距3002公里的干涉仪，臂长4公里，分别位于Hanford和Livingston；意大利VIRGO的干涉仪，臂长3公理；德国GEO600的干涉仪，臂长600米；日本KAGRA的干涉仪，臂长3公理，这是亚洲第一个、也是世界上第一个位于地下的引力波干涉仪，今年2月份开始运行。
十几年前，人们就开始在实验上实施压缩光方案。 2010年， GEO600首先采用了压缩光，对于不低于750Hz的引力波探测提高了敏感度（1Hz代表每秒振动1次）[6,7] 。几年前， LIGO的Hanford探测器也做了压缩光实验，针对黑洞或中子星并合产生的引力波（频率可以低至150Hz），敏感度增加了1倍，而且增大了可探测的频率范围宽度[8] 。
2015年9月14日，LIGO的两个探测器第一次成功探测探测到了引力波。后来， VIRGO也与LIGO联合探测。在前两轮的探测中， LIGO共探测到11次引力波事件，其中， 10次来自黑洞并合， 1次来自中子星并合，而且还与Virgo共同探测了几次，包括第一次探测到中子星并合。
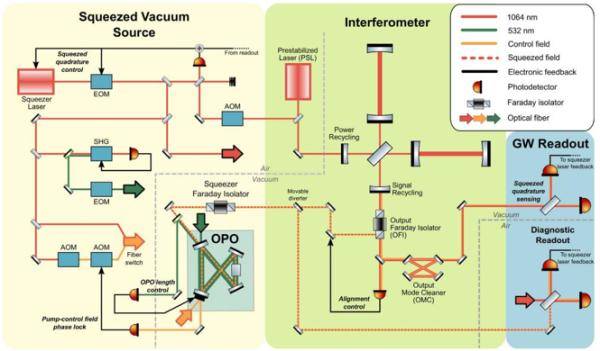
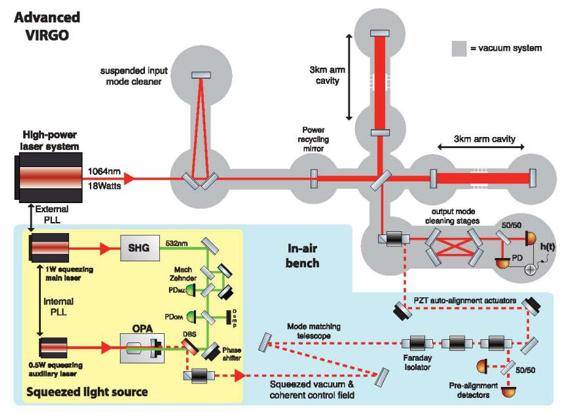
去年4月1日， LIGO的两个探测器和Virgo完成了又一次升级，开始第三轮探测工作，预计持续到明年3月[9] 。这次升级中， LIGO的两个探测器（图3）和Virgo探测器（图4）注入了压缩光[10,11] ，探测器的激光功率也增加了。
因此目前这一轮运行中正在使用压缩光，并作更仔细的探测。这样可以捕捉到更多的引力波，估计比以前增加20%至50% ，有望得到来自超新星或者黑洞与中子星并合产生的引力波，而且将引力波信号实时预警，使得从射电到X射线波段的望远镜可以合作观察这些事件。

文章图片

图3. 目前LIGO干涉仪的示意图，左边是压缩光源[10]

文章图片

图4. 目前Virgo干涉仪的示意图，左下方是压缩光源[11]
事实上，在这一轮运行中， LIGO和Virgo已经得到了一系列观测结果[14] 。首先， LIGO和Virgo探测到一次黑洞并合产生的引力波（GW190412），其中两个黑洞的质量分别是30和8太阳质量，质量比值超过以前所有的情况。然后， LIGO观察到迄今所探测到的最大的引力波事件（GW190521），来自85太阳质量和66太阳质量的两个黑洞并合为142太阳质量的黑洞。这么大的黑洞既超出了以前所知的恒星级黑洞的质量范围，也不属于超大质量黑洞，给相关的天体物理理论提出了挑战。但是也有可能这个引力波源不是黑洞并合。 LIGO和Virgo还探测到26太阳质量的黑洞与2.6太阳质量的天体并合成25太阳质量（GW190814），这也是对理论的一个挑战：一方面，不清楚2.6太阳质量的天体是高质量的中子星还是低质量的黑洞，因为以前认为中子星的最大质量是2.5太阳质量；另一方面，并合前的两个天体质量的比值是迄今最大的。
目前使用的压缩光有一个不足之处，某个频率的散粒噪声得到压缩，但是降低了更低频率的敏感度。最近，研究人员又完成了依赖于频率的压缩[12,13] ，有望下一轮探测（可能在2022年开始）中用上。 LIGO已经宣布，将在今年秋天再次升级[14] 。
2.光原子钟
原子钟是指，原子中的电子改变能量状态时，产生或吸收电磁波，其频率给出时间标准。这个电磁波的频率叫做“跃迁频率” ，就是这两个电子能量状态的能量差除以普朗克常数。频率是单位时间的振动次数，频率的倒数是振动的时间周期。
原子钟是目前最精确的时间和频率标准，用于标准时间的确定、卫星定位，等等。协调世界时（UTC）就是基于国际原子时（IAT），而IAT来自国际上一些互相同步的原子钟所组成的网络，每天误差不超过10?9 秒（即1纳秒）。
1967年，国际度量衡大会用铯原子的最低能量态（叫做“基态”）的两个超精细能量差来定义秒。由于电子与原子核的磁相互作用，原本能量相同的量子态变得能量不一样，之间的差别叫做超精细能量差。著名的氢原子的21厘米线就对应它的超精细能量（对应波长为21厘米，这个波长的电磁波叫做微波）。
以前的原子钟基于常温下原子的微波激射（微波的激光）。但是后来，人们先用激光冷却，将原子温度降到接近绝对零度（0K），然后再在光腔中探测它们。温度或者其他因素引起电磁波谱线有点宽度，也就说频率有误差。这影响原子钟的精确度，所以要降低温度。多次测量并作平均也能进一步提高精度。激光冷却和俘获、高品质光腔、精确的激光光谱、光梳技术带来了原子钟技术的巨大进步。
频率误差不变的情况下，升高频率也降低相对误差。铯原子钟的跃迁频率是9 × 109Hz ，相对精度是10-16[15] 。而可见光频率大概是1014左右，因此光原子钟可以达到更低的相对精度。
实现光原子钟有两个途径。其中一个途径是基于单个离子的冷却和俘获。 2019年，美国国家标准技术研究所（NIST）用铝离子实现了频率相对精度9.4×10-19的光原子钟[16] 。
光原子钟的另一个途径是基于锶、镱等稀土原子。它们的可见光谱线特别窄，提供了稳定、精确的频率标准，比铯原子钟精确千倍。锶还有一个优点，它的原子钟和激光冷却所用的电子能级可以由半导体激光激发电子去占据。
2.1.用光晶格上的一万个锶原子做成的光原子钟
进一步提高精度的一个措施是用量子多粒子系统。对N个全同原子同时测量，使得噪声降低N1/2倍。
好几个研究组用锶的429THz跃迁频率，这是可见光谱线，谱线宽度小于1Hz ，而且通过光晶格上的大量原子来进一步提高精度[17] 。
叶军是NIST与科罗拉多大学博尔德分校共建的联合实验室（JILA）的研究员。 2017年，他的研究组将约1万个锶原子放在3维光晶格中，实现光原子钟，原子的量子相干保持15秒，相对精度达到2.5× 10-19[17,18] 。这个误差相当于宇宙年龄误差100毫秒。
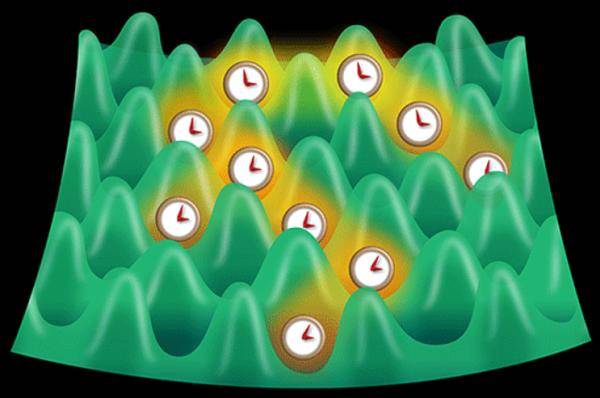
他们先将锶原子冷却到15 nK ，然后将它们移到3维光晶格上。因为接近绝对零度（0K），这些原子处于能量最低状态，叫做“简并费米气体” ，而且处于莫特绝缘体态，也就是说，每个格点位置上只有一个原子，从而避免了原子之间的相互作用（否则会改变跃迁频率）。对于不同格点上原子之间跃迁频率的微小差别（来自不同格点处电磁波能量的微小差别），他们将超精确光谱学与空间成像技术结合起来，修正了这些差别（图5）。这是一项新技术。

文章图片

图5叶军研究组实验的示意图。不同格点上的原子的跃迁频率用钟代表。叶军研究组将超精确光谱学与空间成像技术结合起来，修正了这些差别[17,18] 。
事实上，在此一年前，他们已经实现了3维光晶格上的锶原子的简并费米气体，频率相对精度达到5 × 10–19[19] 。 2017年的这个工作（2018年发表）将精度提高到原来的1.4倍[17,18] 。
这么高的精确度，除了作为原子钟，也可以用来研究量子多体物理，还可以研究基础物理问题,比如基本物理常数是否随时间变化，暗物质探测，广义相对论验证，以及量子引力，也可应用到引力波探测，还有实际的应用，比如提高卫星定位的精度、通过测量重力加速度来进行地质勘探，等等。
2.2.可移动的光晶格光原子钟
但是，在某些应用上，需要解决一些问题，光原子钟才能挑战微波原子钟。比如国际原子时依赖于将各地的原子钟相比较，这是以卫星上的原子钟作中介，而目前卫星上的原子钟使用微波。因此地面上的光原子钟还只能以精度比它低的卫星上的微波原子钟为准。另外，还要考虑地球各处引力场的差异，因为对于10-18的精度，几个厘米的高度差就会体现出引力红移（广义相对论效应）。
因此体积小、可移动的光原子钟才可以在这些应用上取代铯原子钟[15] 。将它们安装到卫星上，才可以提高国际原子时和卫星导航的精度。在地质测量和基础物理方面的应用也需用可移动的光原子钟。但是可移动性降低了精度，因为实验室里的光原子钟依赖于光学平台这样的笨重但稳定的设备。
最近，日本东京大学的香取秀俊与合作者搭建的两个可移动光原子钟（图6）的精度达到了5 × 10-18[15,20] 。这个精度相比之前的可移动光原子钟，提高了1个数量级。它们在户外工作，用光纤联系。

文章图片

图6. 香取秀俊与合作者搭建的两个可移动光原子钟，两个光原子钟用光纤联系起来[20] 。
对于光原子钟的两个途径来说，光晶格可以胜过单个离子，但是光晶格上的原子对于电场扰动更敏感，而产生光晶格的激光、附近的电荷，环境中的黑体辐射都可以产生电场扰动。
2003年，香取秀俊与合作者用锶原子搭建了第一个基于光晶格的光原子钟。在此基础上，他们加强了光原子钟的稳定性。
而在最近的这项工作中[20] ，他们先将锶原子冷却到几微K ，然后将它们放到环形光腔中的一个1维光晶格上。再用激光将俘获原子推到一个黑体辐射屏障中，这个屏障隔离了环境中的黑体辐射。在屏障中，原子完成最后的冷却。用于原子钟的激光尽量准确地调节到跃迁频率。越准确，发生跃迁的原子越多。通过测量激发原子的数目来确定原子钟精度。所有的操作可以通过个人电脑远程控制。
原子钟可用于测量广义相对论效应，也就是引力差异导致的时间差异，即引力红移。据此，目前的GPS卫星定位系统每天调整38皮秒（1皮=10-12）。
以光原子钟的高精度，可以检验广义相对论。广义相对论表明，引力引起的频率相对变化正比于引力势能的差异，比例系数就是光速平方的倒数。如果测量出来的比例系数偏离了光速平方的倒数，就代表对广义相对论的偏离。
香取秀俊与合作者在东京晴空塔，用他们的两个可移动的光原子钟测量了引力红移。他们特意选择了这个并不理想的地点（附近的火车引起的振动较大），以显示设备的抗干扰能力。
他们将一个光原子钟放在塔下，另一个放在450米高处。根据两个光原子钟分别测量到的频率，辅以卫星和激光测量到的高度差，和重力仪在每处测量到的重力加速度，他们得到了比例系数与光速平方倒数的偏离。相对偏离是1.4×10-5 。这是迄今对这个偏离的最好的地面测量，比之前的结果精确了1个数量级，接近相距数千公里的卫星的测量结果。
总结一下今年墨子量子奖获奖人的获奖贡献。 CartonCaves阐明了干涉仪中的量子噪声，并提出利用压缩态来抑制。香取秀俊与合作者搭建了第一个基于光晶格上的锶原子的光原子钟，最近又搭建了可移动的这种光原子钟，精度度达到5×10-18 ，而且用来测量引力红移，检验了广义相对论。叶军与合作者用3维光晶格中的约1万个锶原子实现光原子钟，它们形成简并费米气体，原子的量子相干保持15秒，相对精度高达2.5× 10-19 。
向上滑动阅览【参考文献】
[1] 2020年度墨子量子奖背景和获奖人介绍。
[2] 施郁，引力波的世纪追寻（二）：引力波及其首次探测，科学， 2018 ， 70（4）：15-19.
[3] Carlton M. Caves, Kip S. Thorne, Ronald W. P. Drever,Vernon D. Sandberg, and Mark Zimmermann, Rev. Mod. Phys. 52, 341(1980).
[4] C. M. Caves, Phys. Rev. Lett. 45, 75 (1980).
[5] C. M. Caves, Phys. Rev. D 23, 1693 (1981).
[6] J. Abadie et al. (The LIGO Scientific Collaboration), Nat.Phys. 7, 962 (2011).
[7] H. Grote, et al., Phys. Rev. Lett. 110, 181101 (2013).
[8] J. Aasi et al., Nat. Photon. 7, 613 (2013).
[9] D. Castelvecchi, Nature 568, 4 April, 2019, p.16.
[10] M. Tse et al., Phys. Rev. Lett. 123, 231107 (2019) .
[11] F. Acernese et al. (Virgo Collaboration), Phys. Rev.Lett. 123, 231108 (2019).
[12] Y．Zhao et al., Phys. Rev. Lett. 124, 171101 (2020).
[13] L. McCuller et al., Phys. Rev. Lett. 124, 171102(2020).
[14] LIGO官网， ligo.caltech.edu
[15] C. Middleton, Physics Today 73, 6, 20 (2020).
[16] S.?M. Brewer et al., Phys. Rev. Lett. 123, 033201(2019).
[17] M. Vengalattore, Physics, 11, 22 (2018).
[18] G. Edward Marti et al., Phys. Rev. Lett. 120, 103201(2018).
[19] S. L. Campbell et al., Science 358, 90 (2017).
[20] M. Takamoto et al., Nat. Photonics (2020).

噪声|墨子量子奖解读：引力波与量子精密测量

推荐阅读

自己测心率的正确方法

高血压吃芹菜可以降压吗？高血压吃芹菜有什么影响？

海带土豆汤的做法

柑橘春季要摘心吗

唐山发布事关取暖！唐山三地发布最新消息！

2022国庆节祝福语短信篇二

小学生联欢会主持词小学生联欢会都有什么主持词

剖腹产仰卧起坐好吗？

伟泽的寓意

小乌龟放水里身体浮起来怎么回事

如何用牙膏去除黑头？怎样用牙膏去除黑头？

美味早餐三明治的做法（增肥食谱）

关颖女儿穿比基尼憨态十足关颖近况如何43岁依然俏丽

鹿筋怎样煲汤

喝普洱茶的好处喝普洱茶的好处介绍

丈夫出轨妻子怎么办?如何挽回老公

蜂蜜吃了有哪些好处啊

考研专业课是否都自主命题

格伦霍克酒庄在哪？

卧室空调怎么安装更静音