萧箫 发自 凹非寺
量子位 报道 | 公众号 QbitAI
先来看一道简单的几何问题:
下图中 , 黑圆恰好将红圆的面积等分 , 且黑圆的圆心恰好在红圆上 。 假设红圆半径为R , 黑圆半径为r , 求r 。
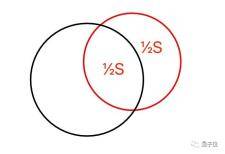
文章图片
是不是感觉已经信手拈来 , 能在纸上演算一通了?
然而 , 就是这个看起来简单的数学难题 , 让数学家们想了几百年 , 都没能给出它的解析解 。
解析解 , 指用精确的数学表达式写出的方程解 。 有些方程难以求出解析解 , 只能写出近似解 。 如下图 , x=cos(x)就没有解析解 , 方程的解只能近似为x≈0.7390…
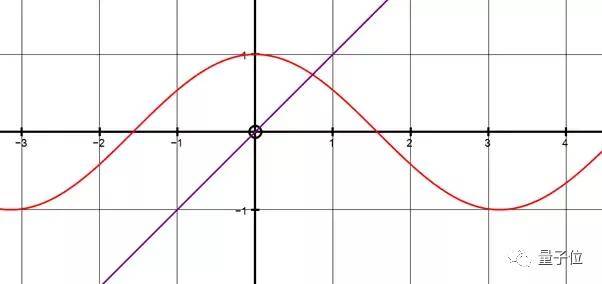
文章图片
△x=cos(x) , x没有解析解
这个难倒数学家的问题 , 叫做「山羊问题」 (goat problem) , 最初的问题描述是这样的:
将一只山羊拴在面积为1英亩的圆形草地的围栏上 , 请问栓多长的绳子 , 才能让山羊刚好吃到半英亩的草?
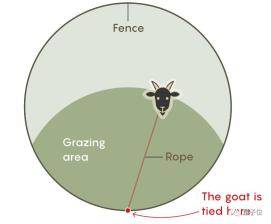
文章图片
问题提出后 , 已有数学家给出了2种求解方程 。
但 , 仅仅是“方程”:
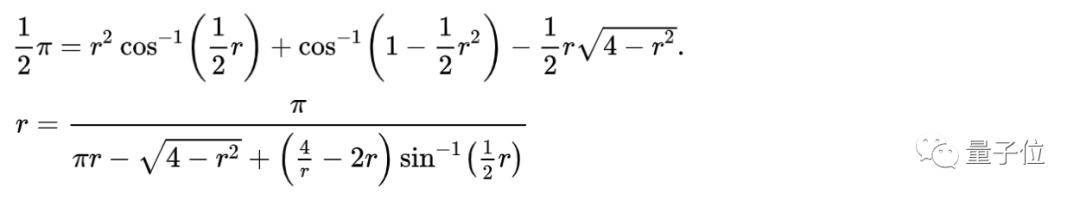
文章图片
这个问题的精确答案 , 即如何准确地用围栏半径来表示绳子长度 , 却一直悬而未解 。
美国海军学院数学家Mark Meyerson曾表示 , 对于这一问题 , 此前“没人知道确切答案 , 解决方法只是大致给出的 。 ”
直到今年 , 才有一位叫做Ingo Ullisch的德国数学家 , 给出了这个问题的解析解 。

文章图片
从迭代到积分 , 求出来的还是方程
如果用数学的语言来描述这个问题 , 它是这样的:
一个半径为R的圆A , 与另一个半径为r的圆B相交 , 其中圆B的圆心在圆A上 , 且两个圆的相交面积为圆A面积的一半 , 求解r 。
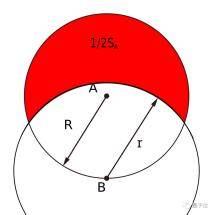
文章图片
如果只是列出有关r的方程 , 目前已经有两种方案 。
第一种方案 , 代入求解透镜面积的方程 。
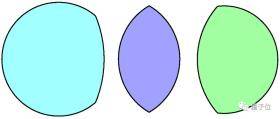
文章图片
透镜由两个(半径相同或不同的)圆相交构成 , 求解它的面积A , 目前已有这么一个公式(其中 , 两圆半径为R和r , 圆心之间的距离为d):
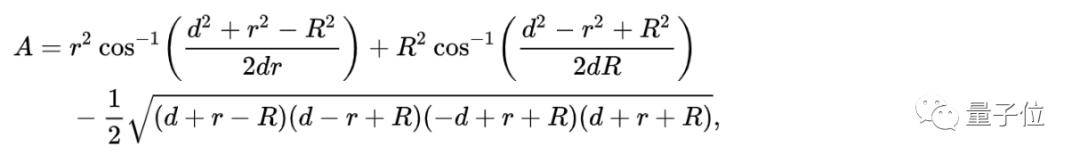
文章图片
显然 , 「山羊问题」也能用透镜面积方程来求解 。
假设围栏的半径为1 , 那么在「山羊问题」中 , 求解条件将变成R=d=1 , 且A=1/2π , 求解出来的r符合这一方程式:
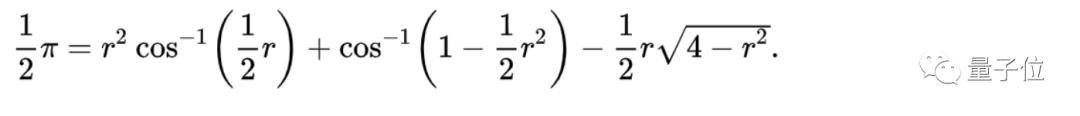
文章图片
这个方程需要用迭代法求解 , 能得到r=1.1587…的答案 。
但这不是数学家想要的结果 。
不愿意就此放弃的数学家们 , 试图用求积分来解决这一问题 , 并给出了第二种方案:
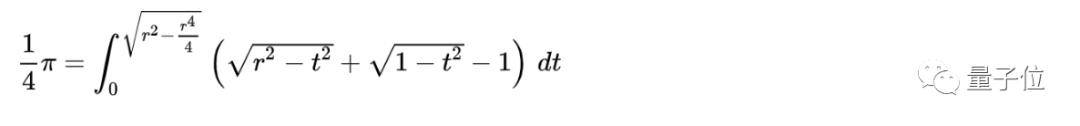
文章图片
这次 , 他们求出了左边有r的式子 , 但遗憾的是 , 这其实是个超越方程 (指方程中有无法用自变数的多项式或开方表示的函数 , 类似于x=cosx):
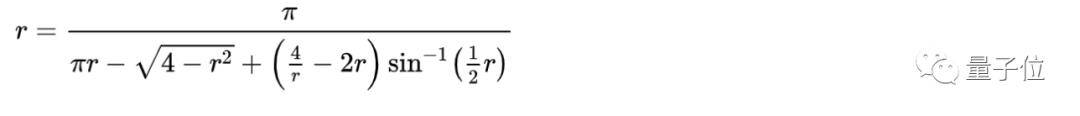
文章图片
这些看似都能求解出r , 但实际上只能算出数值解 , 而非解析解 。
最后用上了复变函数
直到今年 , 一个名为Ingo Ullisch的科学家 , 才终于给出了问题精准的解析解 。
不过 , 为了求解这一问题 , 他甚至用上了复变函数的知识 , 这也使得式子变得复杂不已 。
但也得益于他的贡献 , 这一问题自被提出以来 , 第一次有了解析解:
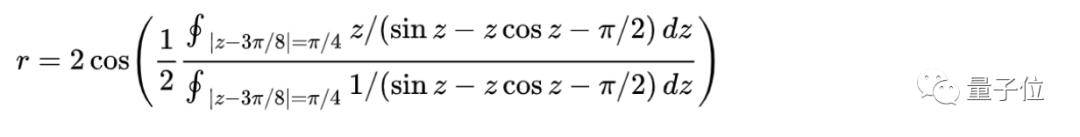
文章图片
那么 , 这个式子是怎么被求解出来的呢?
根据Ullisch的思路 , 他以两个圆的圆心与其中一个交点相连 , 组成了一个三角形 , 如下图所示 。
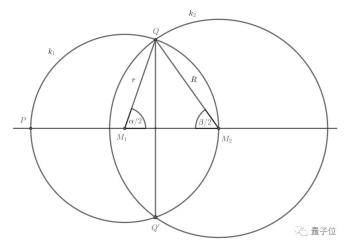
文章图片
其中 , 三角形的两个底角分别被设为α/2和β/2 。
在经过一系列复杂运算后 , Ullisch将式子简化成了下面这个方程:
求解这一方程 , 就能得到解析解 , 但会用到复变函数相关的定理 。
Ullisch表示 , 这一问题之所以复杂 , 是因为问题本质上相当于给定了一个面积固定值 , 并倒推出它的输入 。
但如果想要逆转这一过程 , 反向求解出输入的定义 , 问题就会变得棘手 。
CMU的数学教授Michael Harrison表示 , 这是他所知道的有关「山羊问题」的第一个明确的解析解 。
“这绝对是一个进步 。 ”
这也是山羊问题系列中 , 最原始、最根本 , 也是最难的问题之一 。
有关山羊的问题 , 还有这么多
事实上 , 自1748年来 , 数学家们还从最原始的山羊问题中 , 思考出了各种问题的变体(换着花样找难题做) 。
例如 , 除了让山羊在围栏内吃草 , 还让山羊到围栏外吃草 , 并计算它能吃到的最大草地面积(其中 , 绳索长度和围栏周长固定):
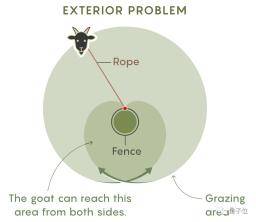
文章图片
此外 , 甚至还让羊飞上了空中 , 让它在三维的世界里吃草(空间中的山羊问题):

文章图片
当然 , 根本问题还是求解球的半径r , 使得两个相交球的相交体积正好是单位球体积的一半 。
不过 , 兰卡斯特大学的数学教授Graham Jameson表示:“三维问题实际上比二维问题更容易解决 。 ”
数学家Fraser表示 , 这是因为 , 如果将问题放在无限的维度中 , 数学家们可以推论出一个更明确的答案 。

文章图片
例如 , 将这个问题放到n维空间时 , Fraser就推算出 , 当n接近无穷大的时候 , 绳子与限定球体的半径比接近于√2 。
然而在二维世界里 , 这种明确的答案反而很难找 。
因此 , 这次Ullisch求出的解析解 , 也是「山羊问题」系列的重大突破 。
不过Ullisch也承认 , 这一问题的解决 , 并不会颠覆教科书或数学的研究 , 因为它只是一个孤立问题 , 不仅与其他问题无关 , 也没有嵌入数学理论 。

文章图片
但数学家们仍然非常激动 。
Mark Meyerson表示:
为数学题寻找新的解法 , 通常是很有价值的 , 这些解法不仅可以再次给已解决的问题带来新思路 , 还可以将之推广到其他问题上 。
数学家Harrison则认为:
虽然解决放牧山羊的问题不会取得突破性的数学成果 , 但数学领域的新方向 , 永远可能来自任何地方 。
而提出山羊问题超越方程的Hoffman , 也有类似的看法:
并非所有的数学进步都来自于取得根本性突破的人 。 有时候 , 这种进步也包括研究经典方法并找到新的角度 , 最终可能会带来意想不到的效果 。
当然 , 网友在祝贺之余 , 也有表示这一问题“不太符合生活常理”的:

文章图片
我认为这个问题 , 是没有山羊相关的经验的人提出的 。 因为我一想到山羊 , 就会想到它们在拼命跳篱笆、嚼绳子……这让我没办法专心解决这个问题 。

文章图片
山羊问题解析解论文:
https://link.springer.com/article/10.1007/s00283-020-09966-0
参考链接:
https://news.ycombinator.com/item?id=25375575
https://www.quantamagazine.org/mathematician-solves-centuries-old-grazing-goat-problem-exactly-20201209/
https://en.wikipedia.org/wiki/Goat_problem#cite_note-1
— 完 —
本文系网易新闻?网易号特色内容激励计划签约账号【量子位】原创内容 , 未经账号授权 , 禁止随意转载 。
_原题《两圆重叠问题你会求解吗?这个问题的准确答案 , 德国数学家最近才找到》
【山羊|两圆重叠问题你会求解吗?这个问题的准确答案,德国数学家最近才找到】阅读原文
推荐阅读
- 人物|扎克伯格将他的山羊取名为“Max”和“比特币” 引发讨论
- 山羊|澳大利亚野山羊泛滥,为什么不引进中国吃货们?怕把它们吃灭绝?
- 系统|ICRA 2020 | 基于无重叠视域车载多相机系统的相对位姿估计方法
- IT之家|特斯拉系统更新Boombox功能可自定义喇叭声音 内置放屁、山羊叫声
- 最新消息|SpaceX对亚马逊做出让步 降低Starlink高度以避免和亚马逊的卫星高度重叠








