误差|IEEE-754浮点格式应用分析_单精度|尾数|格式|测量|binary

IEEE-754是由电子与电气工业协会制定的一整套浮点数表示的标准。本文主要分析最常用的binary32(单精度) ， binary64（双精度可以此类推）。
Binary32占用存储器4bytes ，可以表示最大数值(2?2?23)×2127≈3.402823×1038 ，相比之下， int32(有符号32位整型数)可以表示到2-31-1=2,147,483,647 。在同样的存储宽度下， binary32表示的范围是int32的158,456,293,939,825,284,266,763,033,469.56倍。
Binary32存储结构如下：

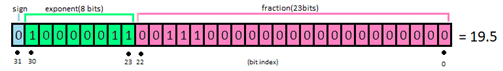
文章图片
IEEE-754浮点格式应用分析
Hex:0x419C0000
二进制表示为:

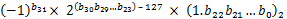
文章图片
二进制表达式
十进制表示为:

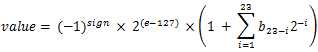
文章图片
十进制表达式
【误差|IEEE-754浮点格式应用分析】value=https://www.sohu.com/a/(-1)0×2(131-127)×(1+2(-3)+2(-4)+2(-5)=(19.5)10
因此，对于每一个浮点数来说，主要有两个部分构成：指数部分和尾数部分。
指数部分有两个特例：即0x00和0xFF
当为0x00时适用如下：(-1)signbit×2-126×0.significandbits即表示±0.0 。此时，尾数部分没有实际的意义。
当为0xFF时表示±infinity 。
尾数部分0～11111111111111111111111b
各位的权值如下：
bit23=1为了节省存储空间此位为隐藏位；
bit22=0.5
bit21=0.25
bit20=0.125
bit19=0.0625
bit18=0.03125
bit0=0.00000011920928955078125
一个整型数，如果用IEEE-754表示可能会有误差。
[-224,224]=[-16777216,16777216] ，没有误差。
[-225,-224]=[-33554432,-16777217]或[16777217,33554432] ，向2倍数舍入。
[-226,-225-1]或[225+1,226] ，向4的倍数舍入。
…
[-2127,-2126-1]或[2126+1,2127] ，向2103的倍数舍入。
[-2128,-2127-1]或[2127+1,2128] ，向2127-23的倍数舍入。
value≤-2128或value≥2128 ，向∞舍入。
要注意数据转化时带来的系统误差，如要克服，就需要综合考虑。

文章图片
计为Uson-11标准型超声波液位计

文章图片
计为Uson-21隔爆型超声波液位计
计为超声波液位计在测量过程中，由于液位的测量要计算声波来回的时间差，而时间差的测量要用到当前环境下的声速。而环境的不同导致声速的不同，在用不同尾数表示声速时，会带给系统一定的误差。为了减小这种系统误差，声速的计算采用的是64bit双精度，保证在计算距离的时候，使公式本身带来的系统误差最小，也整体提高了测量的精度。
同样的例子，输出的4~20mA电流的数值，也需精准表示。在使用当前的距离计算液位，再根据液位计算电流值的情况下，如果使用尾数少的小数表示，可能一次的计算误差几乎可以忽略不计，但经过多次级联的运算后，带来的误差便不可忽视。一些特殊的情况下，可能还会直接影响到测量的精度，为了保证高精度液位的测量，选用双精度是明智的选择。超声波液位计参数介绍（更多产品信息详见：www.jiweimeter.com）

误差|IEEE-754浮点格式应用分析

推荐阅读

被禁止的历史怎么样

农村粘火勺做法

扒皮鱼的营养价值有哪些？扒皮鱼有哪些功效作用？

求经典系统流小说

水磨地面处理有哪些优点

鱼和什么不能一起吃什么食物不能和鱼一起吃

影响网页打开速度的因素有哪些

力推快速祛斑高招美白可以很简单

2022杭州第4期实物配租预登记户租赁入住手续办理地点杭州实物配租申请表

木瓜是什么时间成熟什么季节

花样炒卤面的做法（母婴菜谱）

油炸干是哪儿的特产吗？油炸干介绍

黄花菜该如何种植？黄化菜种植管理技术！

推拿注意事项和禁忌

破云里的经典语录

健脾疏肝治肠易激综合征袁长津谈

子宫切除后可以吃阿胶吗？子宫切除后吃阿胶好吗？

手工十字绣要如何清洗

我的世界砖怎么获得我的世界中怎么获得砖

答的多音字组词