模型|拓端tecdat|R语言极值理论EVT：基于GPD模型的火灾损失分布分析_火灾|seq|理论|数据|log|损失|

原文链接：http://tecdat.cn/?p=21425
极值理论关注风险损失分布的尾部特征,通常用来分析概率罕见的事件,它可以依靠少量样本数据,在总体分布未知的情况下,得到总体分布中极值的变化情况,具有超越样本数据的估计能力。因此,基于GPD(generalized pareto distribution)分布的模型可更有效地利用有限的巨灾损失数据信息,从而成为极值理论当前的主流技术。
针对巨灾发生频率低、损失高、数据不足且具有厚尾性等特点,利用GPD模型对火灾经济损失数据进行了统计建模;并对形状参数及尺度参数进行了估计。模型检验表明,GPD模型对巨灾风险厚尾特点具有较好的拟合效果和拟合精度,为巨灾风险估计的建模及巨灾债券的定价提供了理论依据。
火灾损失数据本文使用的数据是在再保险公司收集的，包括1980年至1990年期间的2167起火灾损失。已对通货膨胀进行了调整。总索赔额已分为建筑物损失、利润损失。

base1=read.table( "dataunivar.txt",
header=TRUE)
base2=read.table( "datamultiva.txt",
header=TRUE)

考虑第一个数据集（到目前为止，我们处理的是单变量极值），

> D=as.Date(as.character(base1$Date),"%m/%d/%Y")
> plot(D,X,type="h")

图表如下：

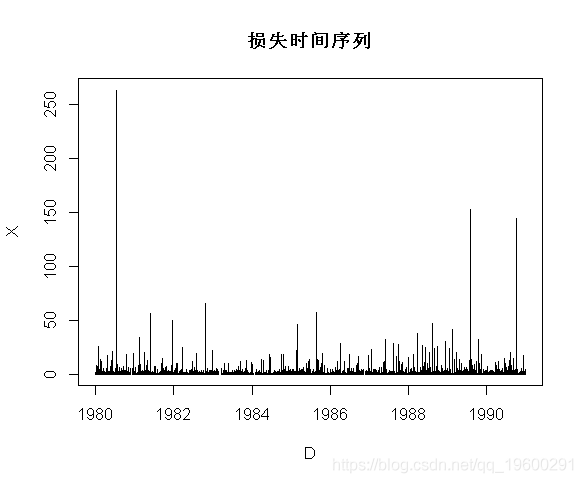
文章图片

然后一个自然的想法是可视化

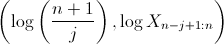
文章图片

例如

> plot(log(Xs),log((n:1)/(n+1)))

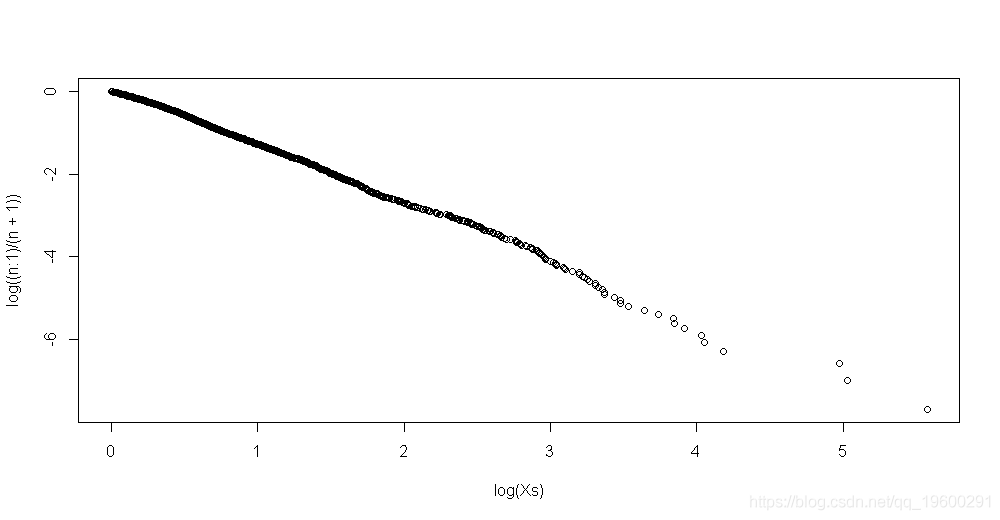
文章图片

线性回归这里的点在一条直线上。斜率可以通过线性回归得到，

lm(formula = Y ~ X, data = https://www.sohu.com/a/B)
lm(Y~X,data=https://www.sohu.com/a/B[(n-500):n,])
lm(formula = Y ~ X, data = https://www.sohu.com/a/B[(n - 100):n, ])

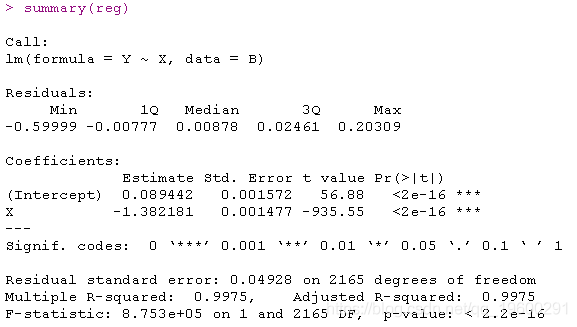
文章图片

文章图片

重尾分布这里的斜率与分布的尾部指数有关。考虑一些重尾分布

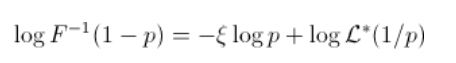
文章图片

由于自然估计量是阶次统计量，因此直线的斜率与尾部指数相反 . 斜率的估计值为（仅考虑最大的观测值）

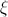
文章图片

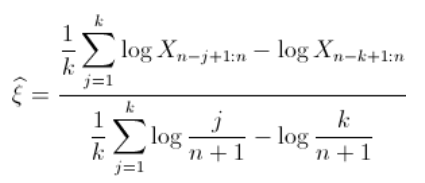
文章图片

希尔估算量希尔估算量基于以下假设：上面的分母几乎为1（即等于）。

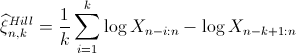
文章图片

那么可以得到收敛性假设。进一步

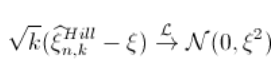
文章图片

基于这个（渐近）分布，可以得到一个（渐近）置信区间

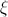
文章图片

> xi=1/(1:n)*cumsum(logXs)-logXs
> xise=1.96/sqrt(1:n)*xi
> polygon(c(1:n,n:1),c(xi+xise,rev(xi-xise)),

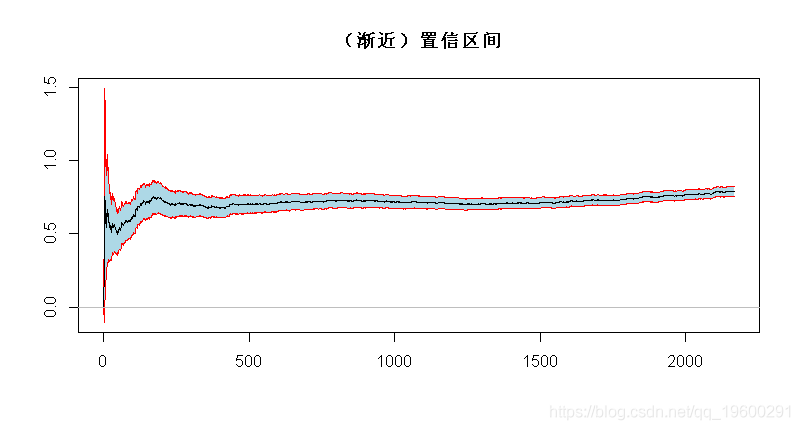
【模型|拓端tecdat|R语言极值理论EVT：基于GPD模型的火灾损失分布分析】

文章图片

增量方法与之类似（同样还有关于收敛速度的附加假设）

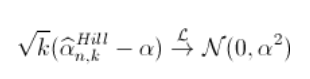
文章图片

（使用增量方法获得）。同样，我们可以使用该结果得出（渐近）置信区间

> alphase=1.96/sqrt(1:n)/xi
> polygon(c(1:n,n:1),c(alpha+alphase,rev(alpha-alphase)),

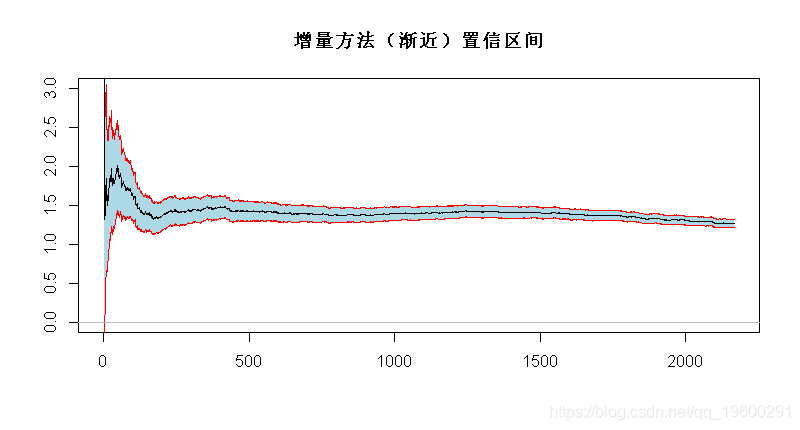
文章图片

Deckers-einmal-de-Haan估计量

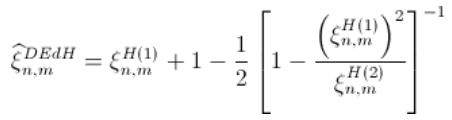
文章图片

然后（再次考虑收敛速度的条件，即），

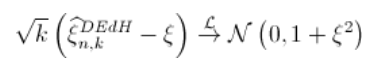
文章图片

Pickands估计

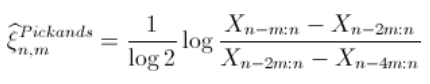
文章图片

由于 ,

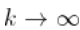
文章图片

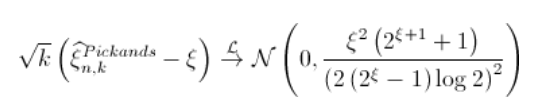
文章图片

代码

> xi=1/log(2)*log( (Xs[seq(1,length=trunc(n/4),by=1)]-
+ Xs[seq(2,length=trunc(n/4),by=2)])/
> xise=1.96/sqrt(seq(1,length=trunc(n/4),by=1))*
+sqrt( xi^2*(2^(xi+1)+1)/((2*(2^xi-1)*log(2))^2))
> polygon(c(seq(1,length=trunc(n/4),by=1),rev(seq(1,

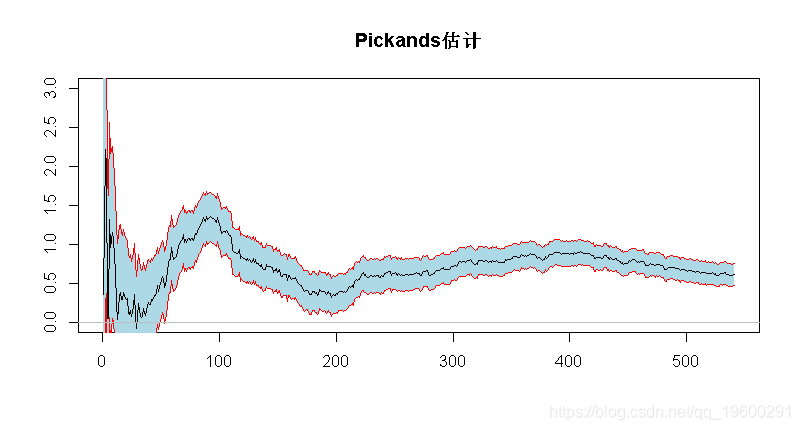
文章图片

拟合GPD分布也可以使用最大似然方法来拟合高阈值上的GPD分布。

> gpd
$n
[1] 2167
$threshold
[1] 5
$p.less.thresh
[1] 0.8827873
$n.exceed
[1] 254
$method
[1] "ml"
$par.ests
xi beta
0.6320499 3.8074817
$par.ses
xi beta
0.1117143 0.4637270
$varcov
[,1] [,2]
[1,] 0.01248007 -0.03203283
[2,] -0.03203283 0.21504269
$information
[1] "observed"
$converged
[1] 0
$nllh.final
[1] 754.1115
attr(,"class")
[1] "gpd"

或等效地

> gpd.fit
$threshold
[1] 5
$nexc
[1] 254
$conv
[1] 0
$nllh
[1] 754.1115
$mle
[1] 3.8078632 0.6315749
$rate
[1] 0.1172127
$se
[1] 0.4636270 0.1116136

它可以可视化尾部指数的轮廓似然性，
> gpd.prof

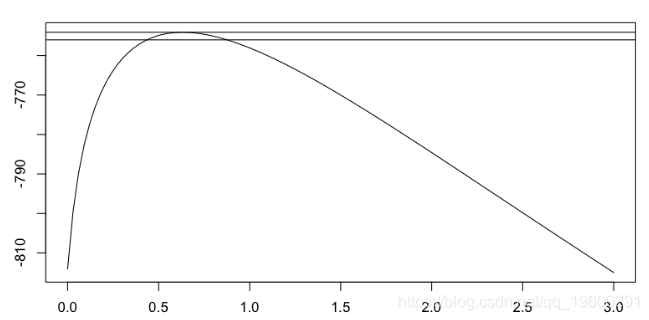
文章图片

或者
> gpd.prof

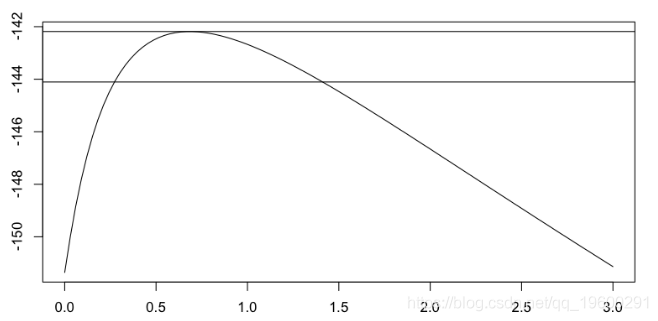
文章图片

因此，可以绘制尾指数的最大似然估计量，作为阈值的函数（包括置信区间），

Vectorize(function(u){gpd(X,u)$par.ests[1]})
plot(u,XI,ylim=c(0,2))
segments(u,XI-1.96*XIS,u,XI+

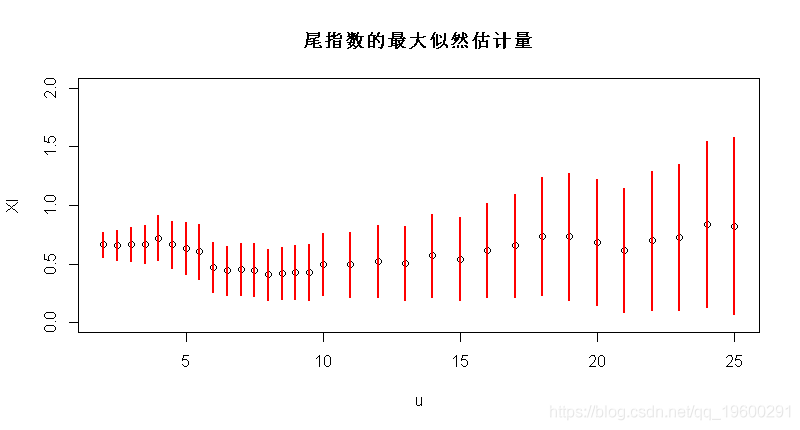
文章图片

最后，可以使用块极大值技术。

gev.fit
$conv
[1] 0
$nllh
[1] 3392.418
$mle
[1] 1.4833484 0.5930190 0.9168128
$se
[1] 0.01507776 0.01866719 0.03035380

尾部指数的估计值是在这里最后一个系数。

文章图片

最受欢迎的见解
1.R语言基于ARMA-GARCH-VaR模型拟合和预测实证研究
2.R语言时变参数VAR随机模型
3.R语言时变参数VAR随机模型
4.R语言基于ARMA-GARCH过程的VAR拟合和预测
5.GARCH（1,1）， MA以及历史模拟法的VaR比较
6.R语言时变参数VAR随机模型
7.R语言实现向量自动回归VAR模型
8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型
9.R语言VAR模型的不同类型的脉冲响应分析

模型|拓端tecdat|R语言极值理论EVT：基于GPD模型的火灾损失分布分析

推荐阅读

化妆后脱妆特别快怎么办

男士冬季面试怎样穿衣服

桂林市动物园在哪

法国蓝菲城堡(窖藏系列)的级别是什么？

传祺gs4钥匙使用方法隐藏功能介绍

邯郸银行属于什么银行

小米6耳机插孔在哪

什么是流量套餐

宁夏银川到内蒙古朱日河有多远

tp-link路由器怎么无线桥接路由器怎么桥接无线

小学转述句的改法技巧学会这几步助你轻松应对转述句改法

新车买保险都有哪些这六种需知道

黑色衣服可以当防晒衣么

南湘为什么要害顾里原因竟然是一个可笑的误会

蒙恰卡怎么养

法兰琳卡三维防晒捍卫肌肤美丽防晒霜啥样的好

豪门宴会经典语录

长卧病人要注意预防褥疮

手动挡踏板使用方法具体需要怎么操作

党员年终述职报告党员述职报告