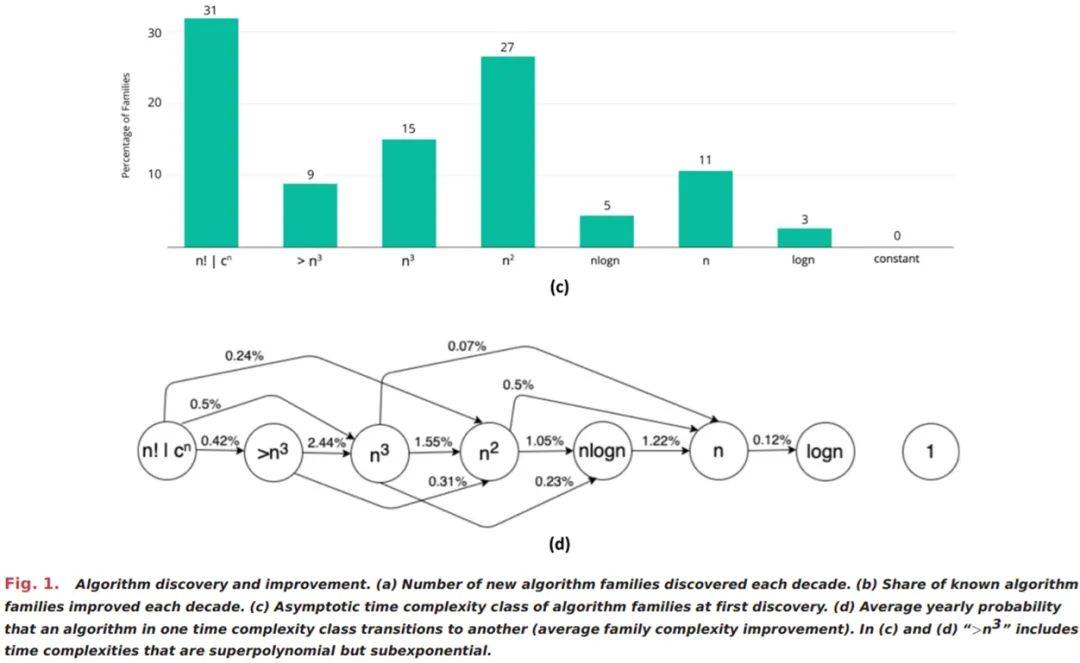
如 1(c) 所示 , 在被发现时 , 31% 的算法族属于指数复杂度类别(表示为 n!|c^n ) 。 这意味着随着输入大小的增长 , 算法至少会进行指数级的运算 。 1(d) 则表明 , 随着算法设计者发现更高效的实现方式 , 算法的复杂度类别会出现重大的转变 。
文章图片
衡量算法改进
随着时间推移 , 算法族的性能会随着「用更少操作解决相同问题的新算法的出现」而提升 。 为了衡量进展 , 研究者着重于提升渐进复杂度的发现 , 例如从 O(n^2) 到 O(n log n) 或者从 O(n^2.9) 到 O(n^2.8) 。
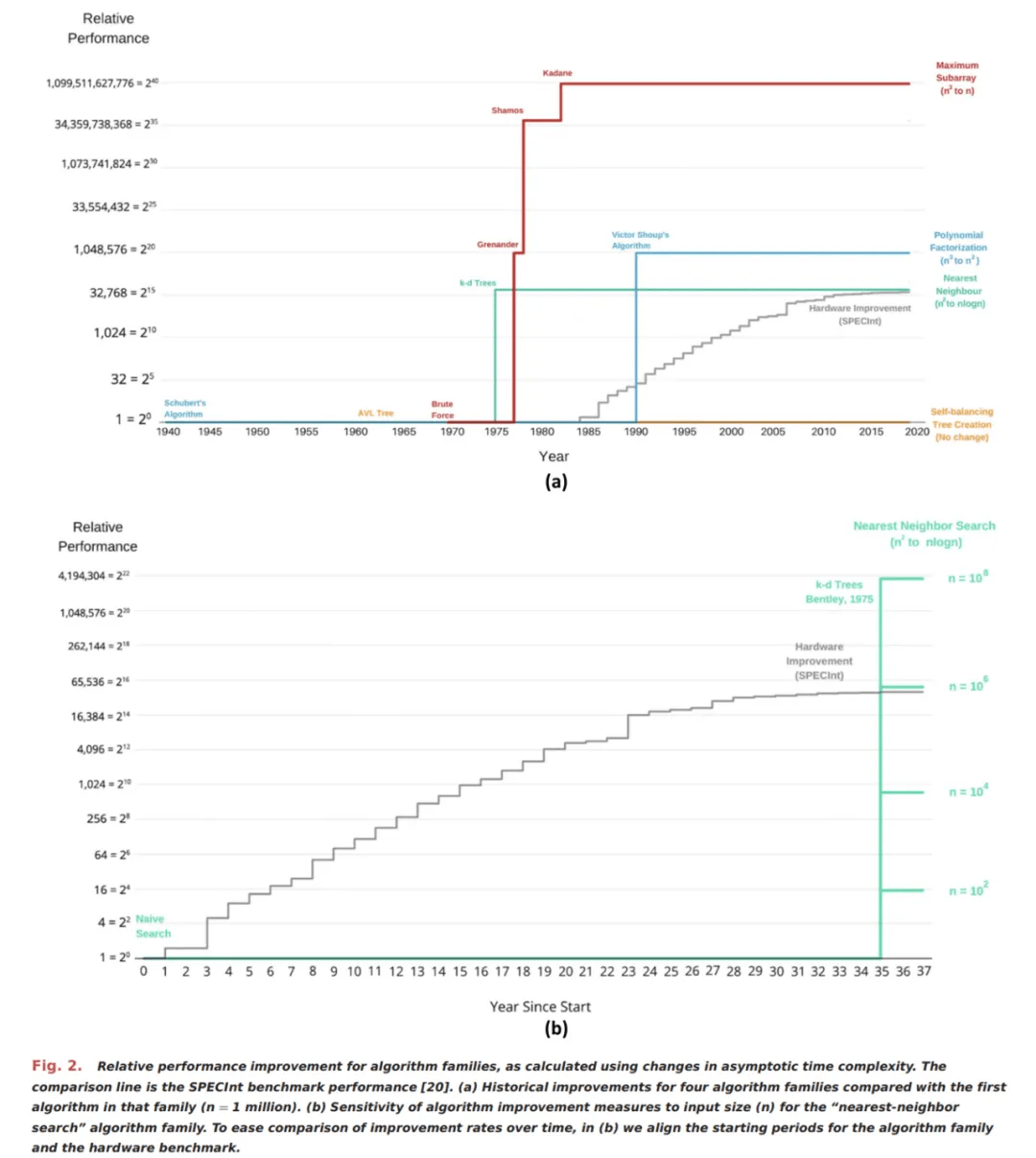
下图 2 (a) 展示了四个不同算法族(不同颜色表示)随时间推移出现的进展 。 对于每个算法族 , 首个算法的性能都被归一化为 1 。 每当发现一种算法具有更高的渐进复杂度时 , 则由垂直步进(vertical step up)表示 。 比如 , 对于 n = 100 万的问题规模而言 , 最大子串等算法的改进速度明显快于硬件或摩尔定律 , 而自平衡树创建等其他算法不呈现这种特点 。
算法和硬件改进之间的重要对比在于改进的可预测性 。 虽然摩尔定律使得硬件随时间推移顺利地改进 , 图 2 展示了那些经历了大的但不频繁的改进的算法 。
此外 , 一种算法的渐进性能关乎于问题输入大小的函数 。 随着输入的增加 , 从一个复杂度类别转变到另一个复杂度类别的改进的规模也在增加 。 图 2(b) 展示了「最近邻搜索」族的这种效果 , 表明当输入大小从 10^2 增加至 10^8 时 , 改进大小也从 15 倍增至约 400 万倍 。
文章图片
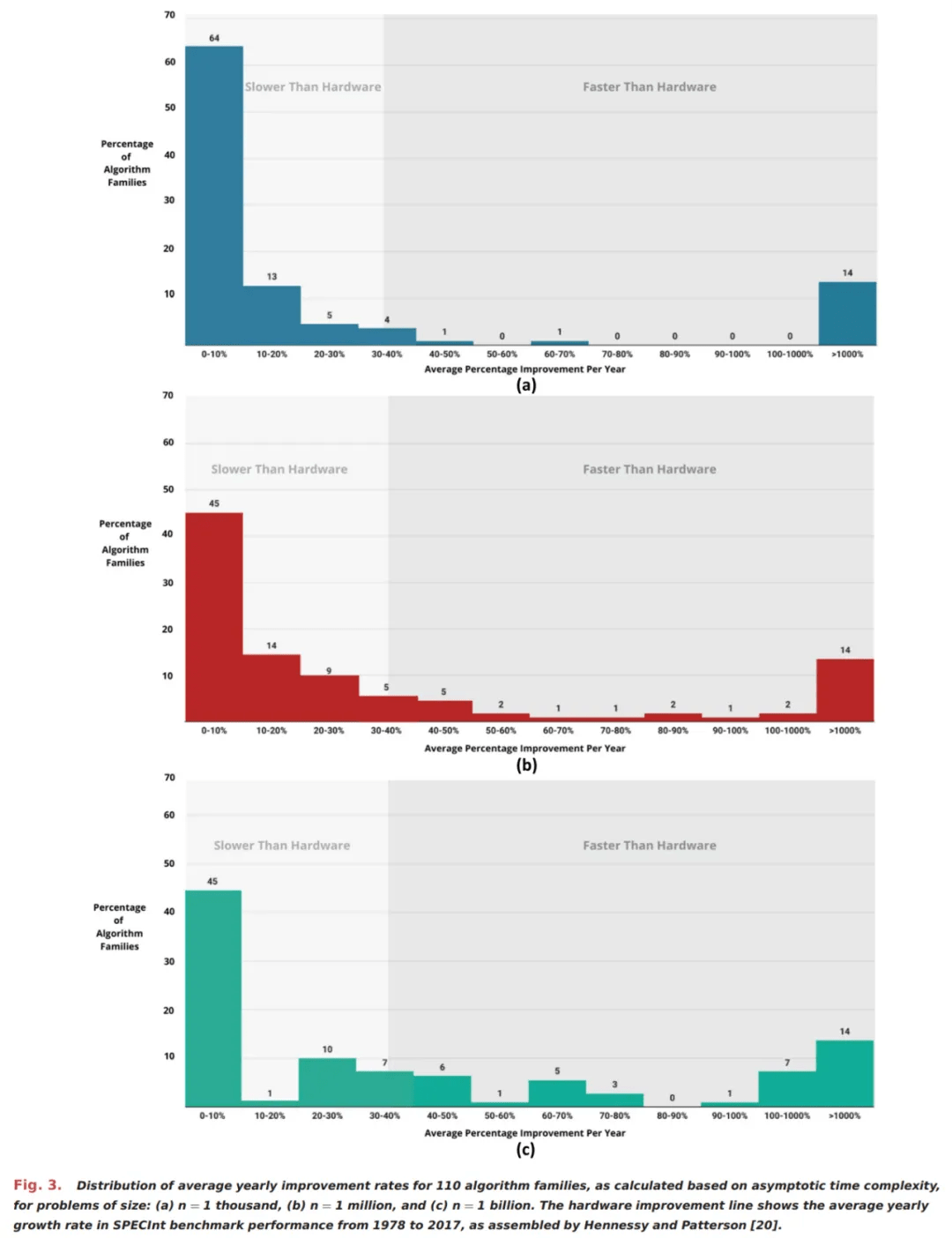
上图 2 展示了算法改进对四个算法族的影响 , 下图 3 将这种分析扩展至了 110 个算法族 。 具体地 , 研究者展示了问题规模分别为 1 千、100 百万和 10 亿时平均年度改进率 , 并将它们与 SPECInt 基准衡量的硬件平均改进率进行比较 。
如下图所示 , 研究者展示了两种大的算法族集群 , 以及一些中间值 。
第一个集群代表不到一半的算法族 , 即使对于大的问题规模而言 , 它们几乎没有出现改进 。 这个集群可能包含那些获得很少关注的算法族、在数学上已经达到最优实现并因而无法进一步改进的算法族、那些仍然无法解决某种大小的问题的算法族或者其他 。
第二个集群包含 14% 的算法族 , 它们的年改进率超过 1000% 。 这些算法受益于指数级加速 , 例如当初始算法具有指数级时间复杂度时 , 后续的改进使得问题可以在多项式时间内解决 。
文章图片
推荐阅读
- 制造业|稳健前行开新局 制造业未来五年转型升级迎来“加速度”
- 设计|宇瞻发布 NOX 系列 DDR5 电竞内存,速度最高 7200MHz
- 数据|全球5G下载速度普遍下降,韩国、中国等除外
- 东西|手机越用越卡?是这5个东西在拖慢你的手机速度!
- 速度|长江存储发布PCle4.0 固态硬盘致态TiPro7000,顺序读取速度高达7400MB/s
- 通信技术|日本将试验激光与卫星通信 连接速度可达10Gbps
- ip|选择HTTP/S还是SOCKS5代理 谁的代理IP稳定速度快
- 长江|致钛新一代国产 SSD 明天发布:Pro 级速度,配备散热器
- Intel|英特尔已为Linux 5.17准备了一些Wi-Fi改进
- 模型|神经辐射场去掉「神经」,训练速度提升100多倍,3D效果质量不减


