易坊好文馆

  1. 首页 > 玩科技 >

模型|这些概念都不懂，别说你会机器学习

数据 实际 概念 训练 模型 机器学习 函数 偏差 规律 方差 QbitAI 预测值

博雯 发自 凹非寺
量子位 报道 | 公众号 QbitAI
机器学习日常：不是在建模 ， 就是在建模的路上 。
而在建模过程中 ， 又能听到炼丹爱好者时而念念有词“怎么又过拟合了？” ， 时而自我安慰“找到偏差和方差的平衡点是成功的诀窍” 。
所以为了能让非专业者也能愉快地玩（zhuang）耍（bi） ， 今天就来科普一下机器学习的几个常见概念 。

模型|这些概念都不懂，别说你会机器学习
文章图片

泛化
如何判别一个每天都刷题的高中班级的成绩怎么样呢？
拉去考一场 。
那怎么判断一个机器学习领域的新算法到底棒不棒呢？
去新数据里溜一圈 。
这种对于训练集以外的数据也能进行良好的判别 ， 或得到合适输出的能力 ， 就称为机器学习模型的泛化（generalization）能力 。
并且 ， 说一个模型泛化能力弱 ， 那也是有很多种弱法的 。
过拟合与欠拟合
有些模型 ， 直接死在提取数据特征这一步 。

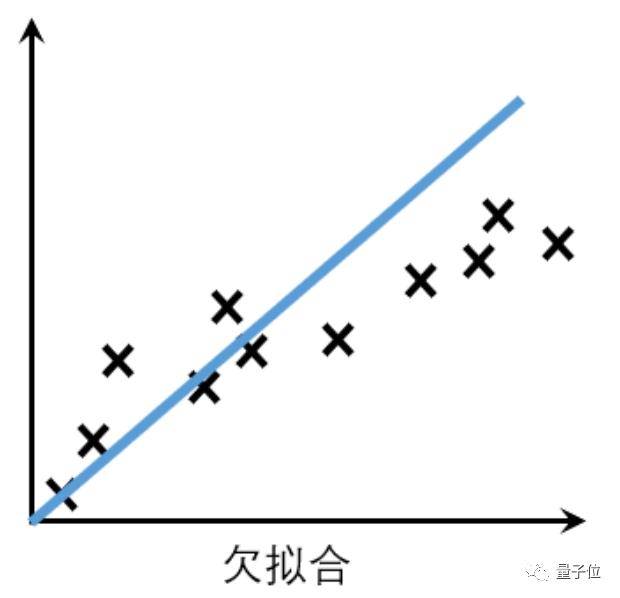
模型|这些概念都不懂，别说你会机器学习
文章图片

训练集上就没有完全拟合数据 ， 实际样本中的表现同样误差很大 。
类似一个高中生每天都拿着五三刷 ， 但是始终找不到做题规律 ， 模拟题做得拉跨 ， 考试就更不用说 。
这种在训练集和测试集（实际样本）中都表现不好的情况 ， 就叫做欠拟合（Underfitting） 。
这通常是因为模型复杂度低引起的（就是菜得很实在） 。
而有些模型在训练时表现良好：

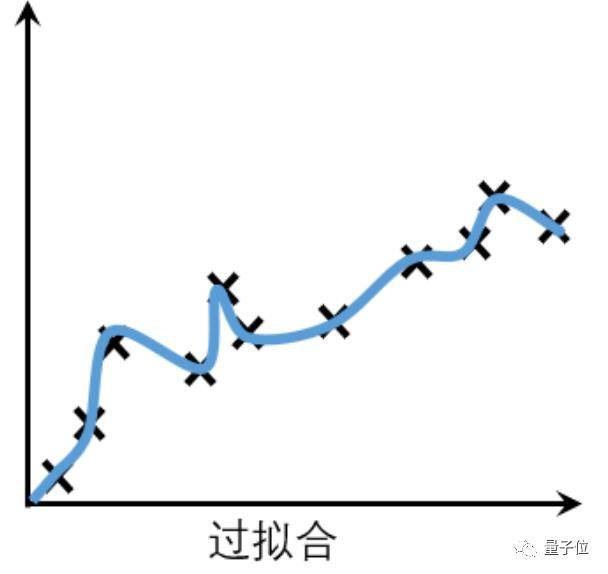
模型|这些概念都不懂，别说你会机器学习
文章图片

但一到实战就扑街 。
这种在训练集上表现良好 ， 但在测试集上表现很差的情况 ， 就叫做过拟合（Overfitting） 。
训练集质量不高就可能导致过拟合 ， 比如样本不足 ， 或者训练数据中的噪声（干扰数据）过多 。
【模型|这些概念都不懂，别说你会机器学习】也有可能因为模型复杂度高于实际问题 ， 只是死记硬背下了训练数据的信息 ， 但完全无法推广到没见过的新数据上 。

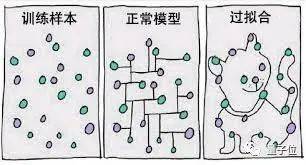
模型|这些概念都不懂，别说你会机器学习
文章图片

不管菜到底有几种方式 ， 对于一个机器模型来说 ， 总归是在实际应用里表现不好 ， 发生了泛化误差（Generalization Error） 。
而这种误差 ， 可以再次细化为两个方面：
误差（Error） = 偏差（Bias） + 方差（Variance）
偏差与方差
在机器学习领域 ， 偏差（bias）是指模型的预测值相对于真实结果的偏离程度 。
△其中f(x)为预测函数 ， y为样本数据真实值
而方差（variance）与真实值没有关系 ， 只描述通过模型得到的预测值之间的分布情况 。
对于一个模型来说 ， 偏差反映模型本身的精确度 ， 而方差则衡量模型的稳定性 。

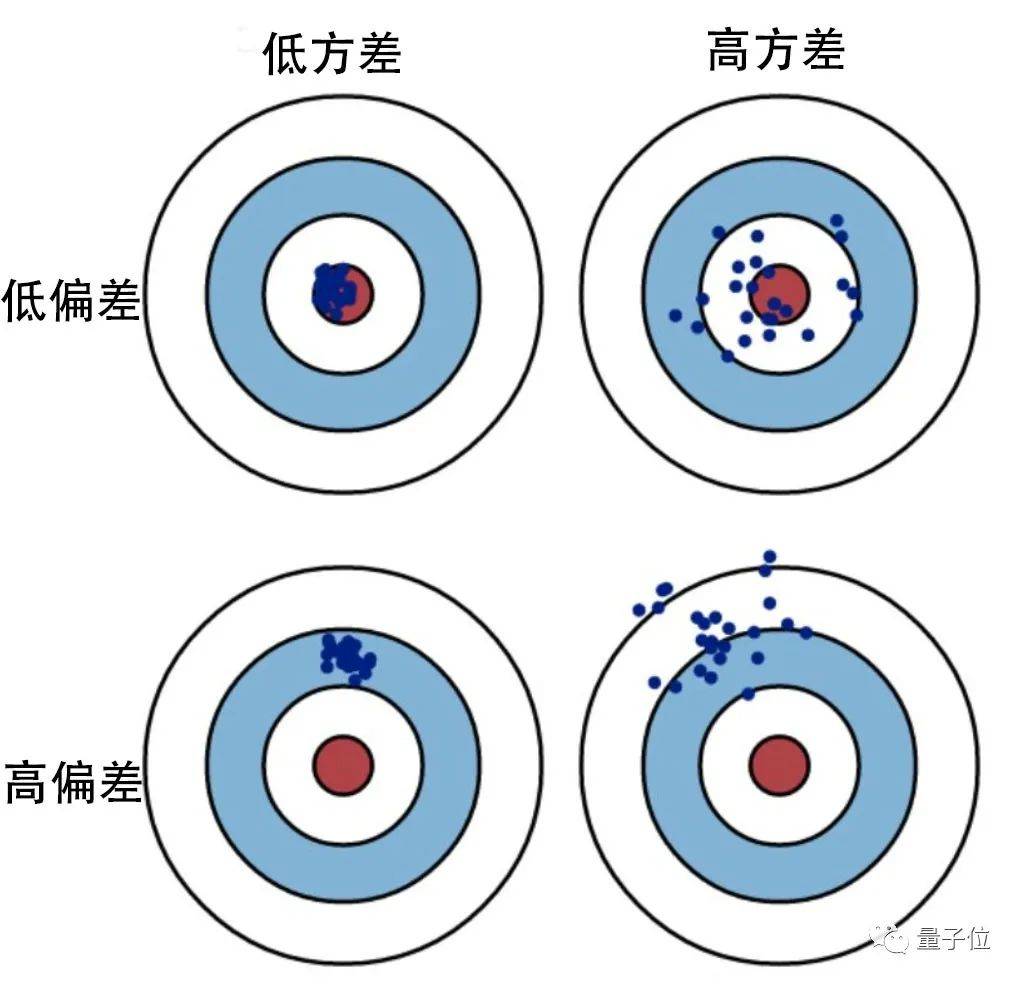
模型|这些概念都不懂，别说你会机器学习
文章图片

如果模型过于简单且参数很少 ， 那么它可能具有高偏差和低方差的特征 ， 也就会造成欠拟合 。
而如果模型复杂而具有大量参数 ， 那么它将具有高方差和低偏差的特征 ， 造成过拟合 。
看上去 ， 一个好的机器模型就是要同时追求更低的偏差和方差 。
但在实际应用中 ， 偏差和方差往往不可兼得 。
偏差与方差的权衡
先来看这两个模型：

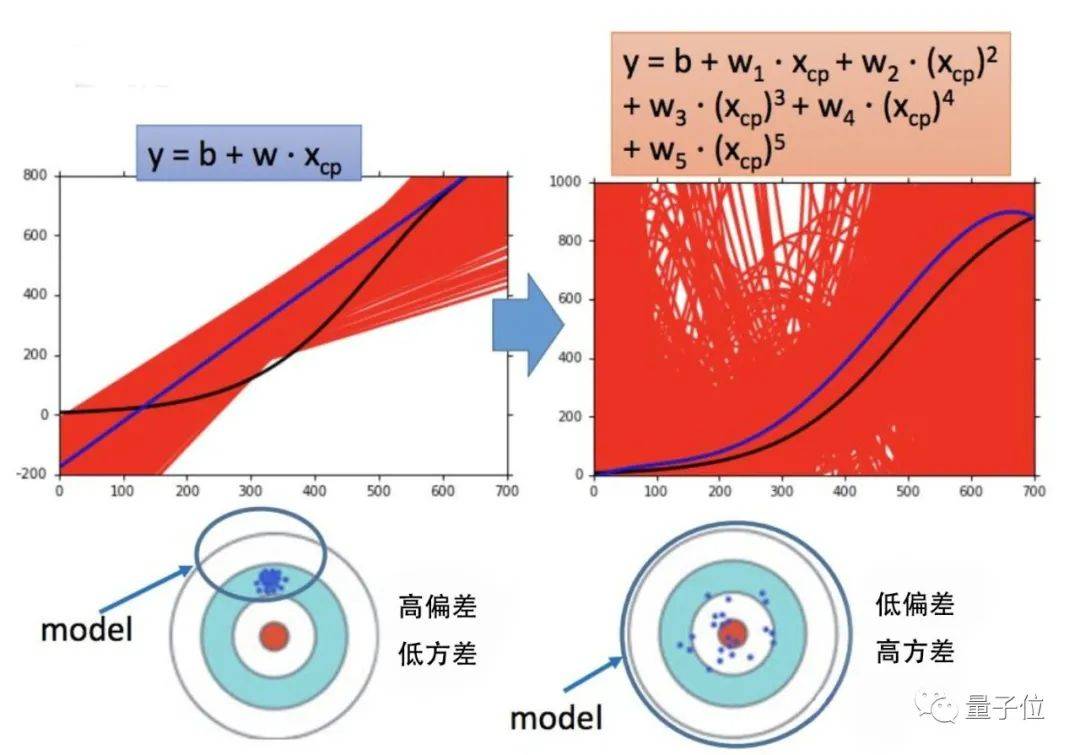
模型|这些概念都不懂，别说你会机器学习
文章图片

右边的模型明显比左边要复杂很多 ， 也因此它的偏差更低 ， 方差更高 ， 与左边的模型相反 。
这种偏差与方差之间的冲突就是偏差-方差窘境（Bias- Variance dilemma）：

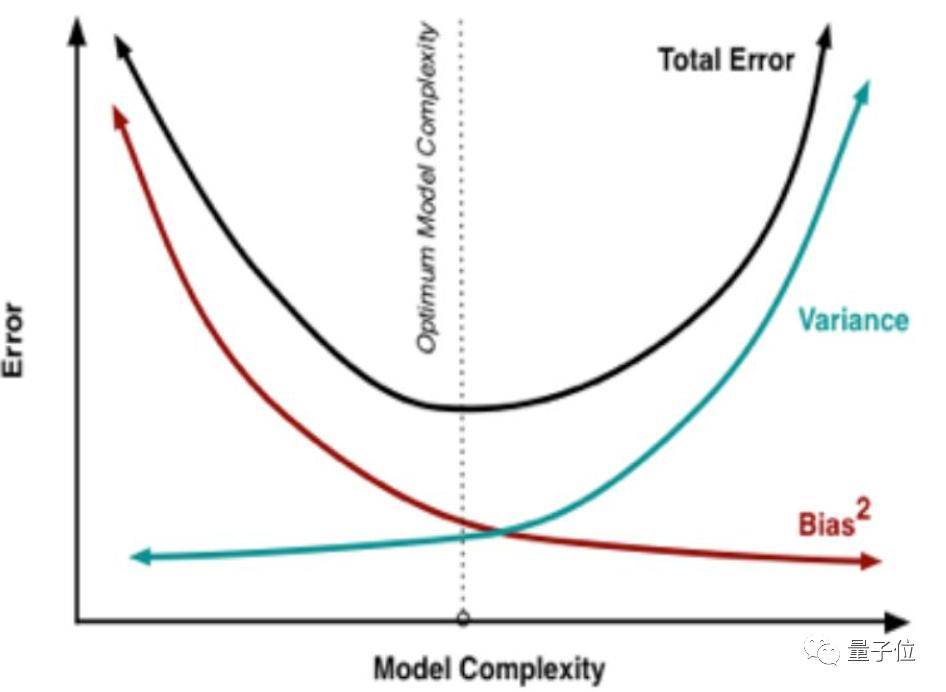
模型|这些概念都不懂，别说你会机器学习
文章图片

在改进算法时 ， 要减少偏差就会增大方差 ， 反之亦然 。
因此 ， 我们需要找到一个合适的平衡点 ， 既不会因为高偏差而造成欠拟合 ， 也不会因为高方差而造成过拟合 。
这种偏差与方差之间的权衡（bias and variance trade-off） ， 实际上也就是模型复杂度的权衡 。
为什么要提出这些概念？
简单来说 ， 为了让计算机也学会人类的概括能力 。
比如 ， 如果我们要通过某地房屋面积与房价之间的关系 ， 进而帮助房屋售卖者选取更合适的售价 ， 那么下面哪个函数最好呢？

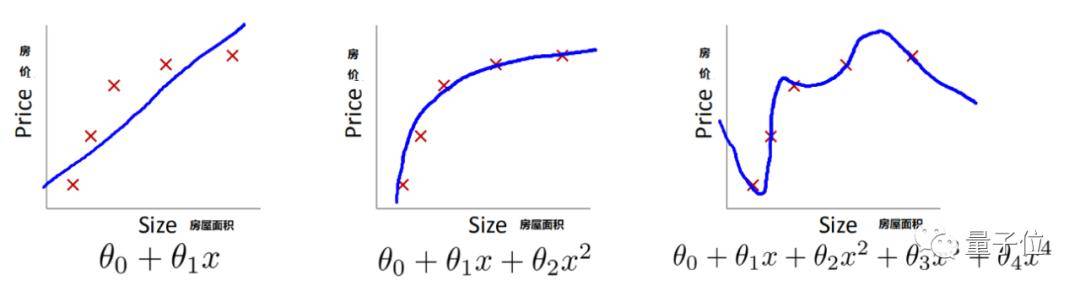
模型|这些概念都不懂，别说你会机器学习
文章图片

△红色为事先给定的样本数据
第一个明显欠拟合 。 都没有从给定的数据中找到一般规律 ， 更不用说让函数去预测新房价面积可能对应的售价了 。
第三个就是过拟合 ， 函数参数过多 ， 想要抓住所变化 ， 反而导致模型的通用性下降 ， 预测效果大打折扣 。
而第二个函数基本拟合了样本数据 ， 形成了一般规律 ， 也保证了对新数据的预测能力 。
能从海量数据中找到一般规律 ， 这就是一个模型的泛化能力 。
模型的泛化能力越高 ， 通用性也就越强 ， 这样能完成的任务范围也就越广 。
但就算是ANN（人工神经网络）这样优秀的机器学习模型 ， 目前也还是受限于偏差与方差的权衡 。
算法工程师们提出了各种方法 ， 如正则化（Regularization)、套袋法（Bagging）、贝叶斯法（Bayesian) ， 使模型能够更好地概括旧数据 ， 预测新数据 。
并期望着最终能构建一个机器学习模型 ， 使其能力无限逼近目前最强的通用模型——人类大脑 。
参考链接：
[1]https://towardsdatascience.com/the-relationship-between-bias-variance-overfitting-generalisation-in-machine-learning-models-fb78614a3f1e
— 完 —
本文系网易新闻?网易号特色内容激励计划签约账号【量子位】原创内容 ， 未经账号授权 ， 禁止随意转载 。
_原题《这些概念都不懂 ， 别说你会机器学习》
阅读原文

    推荐阅读


    上一篇：自然环境|鸟儿爱嗦螺，是怎么把蜗牛变得五颜六色的？

    下一篇：IT|波音无人机首次成功在空中为另一架飞机加油