定理|三角函数是必考题，如何学会？先把这块基础抓好_三角形|基础|必考题|正弦|面积

文章图片

高中数学，在引入正弦定理内容时，提出在任意三角形中有大边对大角，小边对小角的边角关系。我们是否能得到这个边、角的关系准确量化的表示呢?
在引入余弦定理内容时，则会提出探究性问题如果已知三角形的两条边及其所夹的角,根据三角形全等的判定方法，这个三角形是大小、形状完全确定的三角形。
依据已知条件中的边角关系判断三角形的形状时，主要有如下两种方法：
(1)利用正、余弦定理把已知条件转化为边边关系，通过因式分解、配方等得出边的相应关系，从而判断三角形的形状；
(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系，通过三角函数恒等变形，得出内角的关系，从而判断出三角形的形状，此时要注意应用A＋B＋C＝π这个结论。
注意：在上述两种方法的等式变形中，一般两边不要约去公因式，应移项提取公因式，以免漏解。
三角函数历来是高考重点热点之一，题型有选择填空和解答题，难度上相对容易，一般位于中档题，只要大家掌握好三角函数公式，利用公式化简解析式并求性质，三角函数类问题就能解决。

文章图片

三角函数高考题型虽然不难，但内容却比较丰富，如包含三角函数的图像与性质、三角函数恒等变化、诱导公式等等。因此，我们学习三角函数，一定要特别注意对它的化简、计算以及证明的恒等变形的方法的积累与应用。今天我们就来讲讲三角函数的图像与性质这一块内容。
正弦定理和余弦定理有关的高考试题，典型例题1：
如图，在△ABC中，点P在BC边上， ∠PAC=60° ， PC=2 ， AP+AC=4．
【定理|三角函数是必考题，如何学会？先把这块基础抓好】（Ⅰ）求∠ACP；
（Ⅱ）若△APB的面积是3√3/2 ，求sin∠BAP．

文章图片

文章图片

考点分析：
余弦定理；正弦定理．
题干分析：
（Ⅰ）在△APC中，由余弦定理得AP2﹣4AP+4=0 ，解得AP=2 ，可得△APC是等边三角形，即可得解．
（Ⅱ）法1：由已知可求∠APB=120°．利用三角形面积公式可求PB=3．进而利用余弦定理可求AB ，在△APB中，由正弦定理可求sin∠BAP=3sin120°/√19的值．
法2：作AD⊥BC ，垂足为D ，可求：PD=1 ， AD=√3 ， ∠PAD=30° ，利用三角形面积公式可求PB ，进而可求BD ， AB ，利用三角函数的定义可求sin∠BAD=BD/AB=4/√19 ， cos∠BAD=AD/AB=√3/√19．利用两角差的正弦函数公式可求sin∠BAP=sin（∠BAD﹣30°）的值．

文章图片

正弦定理和余弦定理有关的高考试题，典型例题2：
在△ABC中，角A ， B ， C的对边分别为a ， b ， c ，且2acosB=2c﹣√3b．
（1）求cos（A+π/4）的值；
（2）若∠B=π/6 ， D在BC边上，且满足BD=2DC ， AD=√13 ，求△ABC的面积．

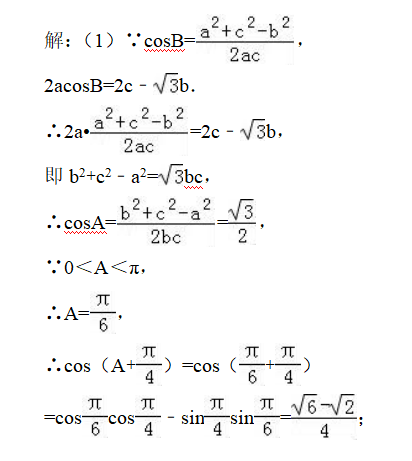
文章图片

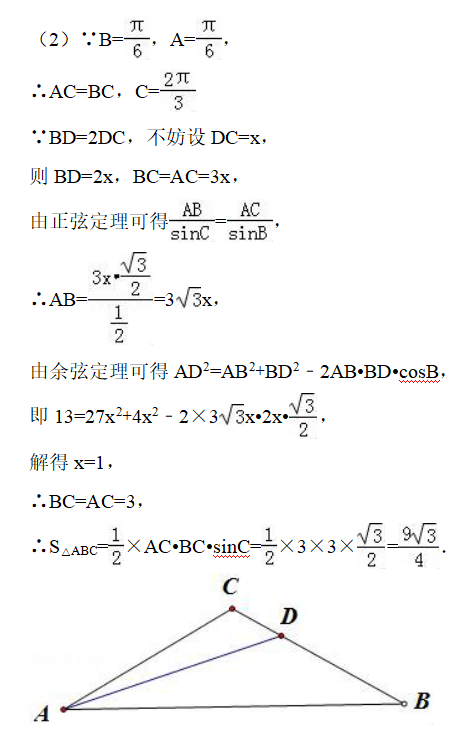
文章图片

考点分析：
三角形中的几何计算．
题干分析：
（1）根据余弦定理表示出cosB ，再根据条件可得b2+c2﹣a2=√3bc ，再利用夹角公式级即可求出A ，再根据两角和的余弦公式即可求出，
（2）不妨设DC=x ，则BD=2x ， BC=AC=3x ，根据正弦定理和余弦定理即可求出x ，再根据三角形的面积公式计算即可。

文章图片

正弦定理和余弦定理有关的高考试题，典型例题3：
在△ABC中，角A、B、C所对的边分别是a、b、c ，已知sinB+sinC=msinA（m∈R），且a2﹣4bc=0．
（1）当a=2 ， m=5/4时，求b、c的值；
（2）若角A为锐角，求m的取值范围．

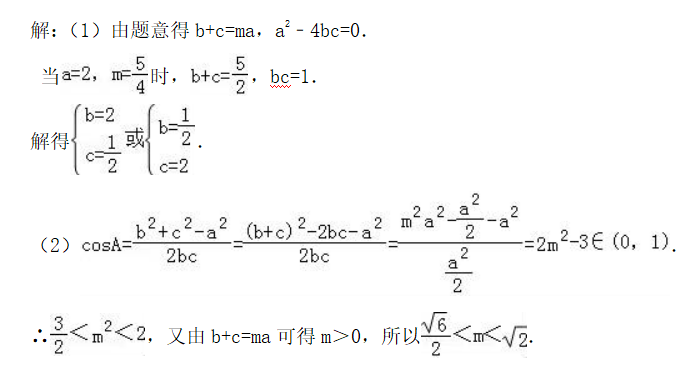
文章图片

考点分析：
余弦定理．
题干分析：
（1）sinB+sinC=msinA（m∈R），利用正弦定理可得：b+c=ma ，且a2﹣4bc=0．a=2 ， m=5/4时，代入解出即可得出．
（2）利用余弦定理、不等式的解法即可得出．

定理|三角函数是必考题，如何学会？先把这块基础抓好

推荐阅读

六大洁面注意事项泡沫洗面奶不是人人都适用

脾酒和白酒为什么不能掺着喝？

怎样祛除牙齿烟渍？

百香果繁殖时间方法百香果怎么种植

哪些国家以前是法国的殖民地

羽毛球杀球技巧

计算程序中flag是什么意思

桔子和橘子的区别是什么

然褚沛文 15岁女孩被扇50耳光，因没及时应答同学，打人者戾气从哪里来

中药养生茶饮有哪些

清晨早安暖心寄语 2020漂亮动态早上好祝福表情图片分享

洗衣人酒店布草发灰缘由！

女人月经期吃什么好

灿然和粲然的意思

附地菜的功效与作用附地菜的食用禁忌

微信怎么修改地址名称

意大利蒙特罗索干白葡萄酒怎么样？

炸油香怎么做又软又好吃

现货黄金的交易规则现货黄金如何买卖交易

孔子所说的话对世人的影响