
文章图片
什么是数列?
数列是指按照一定顺序排列的一列数 。
什么是数列的项?
数列的项是指数列中的每一个数 。
什么是数列的通项公式?
如果数列{an}的第n项与序号n之间的关系可以用一个式子来表示 , 那么这个公式叫做这个数列的通项公式 。
什么是数列的递推公式?
如果已知数列{an}的首项(或前几项) , 且任一项an与它的前一项an-1(n≥2)(或前几项)间的关系可用一个公式来表示 , 那么这个公式叫数列的递推公式 。
从历年高考数学题型来看 , 数列可以和函数、方程、不等式、三角等相关知识进行“串联” , 形成更为复杂的综合性问题;或是结合实际生活例子 , 考查考生运用数列知识解决实际问题的能力 。

文章图片
数列有关的高考试题分析 , 典型例题1:
设等差数列{an}满足3a8=5a15 , 且a?>0 , Sn为其前n项和 , 则数列{Sn}的最大项为( )
A.S23
B.S24
C.S25
D.S26
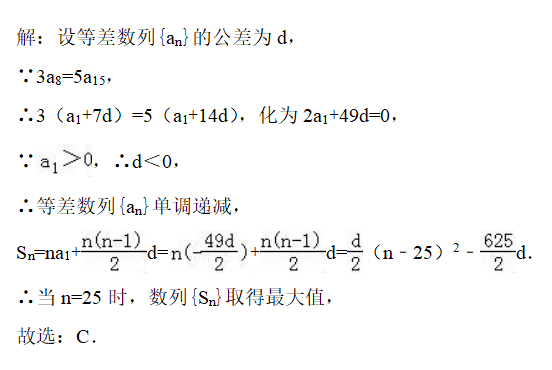
文章图片
考点分析:
等差数列的前n项和.
题干分析:
设等差数列{an}的公差为d , 由3a8=5a15 , 利用通项公式化为2a1+49d=0 , 由a?>0 , 可得d<0 , Sn=na1+n(n-1)d/2=d(n﹣25)2/2﹣625d/2.利用二次函数的单调性即可得出.
数列有关的高考试题分析 , 典型例题2:
设数列{an+1}是一个各项均为正数的等比数列 , 已知a3=7 , a7=127.
(1)求的a1值;
(2)求数列{an}的前n项和.

文章图片
考点分析:
数列的求和.
题干分析:
(I)利用等比数列的通项公式及其性质即可得出.
(II)利用等比数列的求和公式即可得出.

文章图片
数列有关的高考试题分析 , 典型例题3:
在等差数列{an}中 , a10=a14﹣6 , 则数列{an}的前11项和等于( )
A.132
B.66
C.﹣132
D.﹣66
解:∵数列{an}为等差数列 , 设其公差为d ,
∵a10=a14﹣6 ,
∴a1+9d=(a1+13d)﹣6 ,
∴a1+5d=﹣12 , 即a6=﹣12.
∴数列{an}的前11项和S11=a1+a2+…+a11
=(a1+a11)+(a2+a10)+…+(a5+a7)+a6
=11a6
=﹣132.
故选:C.
考点分析:
等差数列的前n项和;等差数列的通项公式.
题干分析:
设其公差为d , 利用等差数列的通项公式得到a6=﹣12.所以由等差数列的性质求得其前n项和即可.

文章图片
数列有关的高考试题分析 , 典型例题4:
已知数列{an}的前n项和为Sn , a1=1 , 且3Sn=an+1﹣1.
(1)求数列{an}的通项公式;
(2)设等差数列{bn}的前n项和为Tn , a2=b2 , T4=1+S3 , 求1/b?·b?+1/b?·b3+……+1/b10·b11的值.
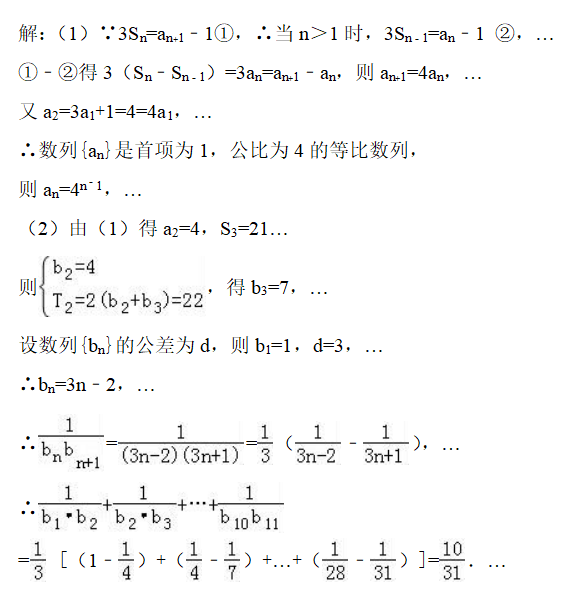
文章图片
考点分析:
数列递推式;数列的求和.
题干分析:
(1)利用递推关系a1=1 , 且3Sn=an+1﹣1 , 可得当n>1时 , 3Sn﹣1=an﹣1 , 两式相减 , 可得an+1=4an(n≥2) , 再验证n=1的情况 , 即可判断数列{an}是首项为1 , 公比为4的等比数列 , 从而可求数列{an}的通项公式;
【高考|吃透数列,学好数学,才能为高考提分】(2)依题意 , 可求得bn=3n﹣2 , 利用裂项法可得1/bnbn+1=(1/3n-2﹣1/3n+1)/3 , 于是可求1/b?·b?+1/b?·b3+……+1/b10·b11的值.
推荐阅读
- 月球|【2022高考倒计时176天】努力是为了看到不一样的风景
- 遗传|【2022高考倒计时178天】高考完就可以去看山和海了
- 最新消息|江西高考取消文理分科:全新3+1+2模式 总分750
- 最新消息|安徽新高考方案公布将取消文理分科:学生选择科目余地更大
- 人物|高考623分外卖小哥已入学报到:四年前退学 不读书选择非常少
- 人物|高考移民考入复旦被开除后起诉学校 三审都判败诉
- 最新消息|上海中高考英语将降至50分?教委回应称消息不实
- 技术|2022年高考作文预测:置之死地而后生
- 灾难|挥不去的高考梦魇,也许只是你逃避生活的借口
- 最新消息|华科回应网红称可以靠关系转学:录取符合高考政策 其父母非教职工







