调节|时差反应东西向不对称性的解释_时差|进行|时区|现象|等式|知识

作者：Thomas M. Antonsen等
翻译，独行者，哆嗒数学网翻译组成员。
关注哆嗒数学网每天获得更多数学趣文
时差反应是搭乘飞机旅行的人在跨越多个时区后常常出现的现象。经典症状包括头晕、恶心、在当地出现白天醒不了、晚上睡不着。用简单的话来说，人体内的时间调节机制一般会与当地的24小时昼夜周期相适应，这一般取决于外部自然条件（特别是日出日落）和社会条件。由于快速地跨越了多个时区，身体内的昼夜节律调节机制需要时间去与所在地的外部自然昼夜周期进行同步；这种重新同步机制的现象便是旅客们所表现的时差反应现象。由于节律器的重新同步是一种动态机制，这便促使人们从动态系统的角度进行数学建模，并尝试解释这一现象。

文章图片

当身体产生许多信号来帮助调节身体的昼夜周期时，身体当中的一个部位似乎起着非常重要的作用：视交叉上核（the suprachiasmatic nucleus ， SCN），这是人体大脑中一个非常狭小的部位。医学研究发现视交叉上核是由104个调节神经元组成的一个序列，所以我们也就可以有理由认为如果把这些神经元单独隔离开来，这些生命调节器的周期大致在一个平均值上，通常情况下其平均时间在24小时以上。当这些神经元组合在一起的时候，这些生命节律调节器便会进行相互协调，同时当其中一个神经元受到外界刺激后，他会通知其他神经元进行调节。就比如，太阳的升起和落下。这些结论是我们构建模型和预测分析的基础概念，同时也是其他研究者的基本思路。但是我们所构建的模型与之前的研究者有所不同，我们着眼于组合在一起的每一个的视交叉上核神经元的微观状态，并将忽略高维度微观结构，将我们的研究缩减到低维度的宏观结构以便进行观察。我们建立模型主要是为了解释相比于向西跨越相同数量时区，时差反应在向东跨越同样数量的时区后将会更加严重（例如，恢复时间更长）的现象，因为这是人们普遍的感受。特别的，我们分析视交叉上核的平均昼夜周期略大于24小时现象对于东西时差反应不对称现象的解释有多少可信度。
在决定去了解在N个神经视交叉上核集合中去分析跨时区旅行和时区重新同步之间的相互作用之初，我们使用了一个非常简单的模型来分析这些神经元的作用，这是考虑到了部分现实情况。藏本模型（Kuramoto model）是一个非常出名的模型，在这个模型中每一个神经视交叉上核的复杂动态变化都会被简化成一个简单的时间和相相关的演化方程θi(t),i表达的是在第i个视神经交叉上核的状态。其中i=1,2,3,……N. 而视神经交叉上核的相则会在时间上提前一点。根据下面的公式可以得出各个变量之间的关系：

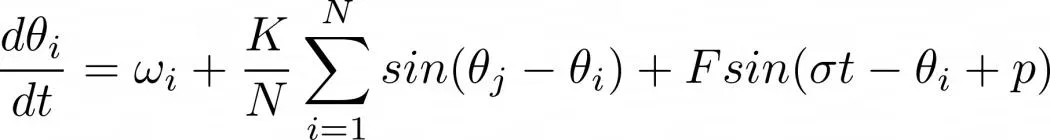
文章图片

其中， ωi是每个视神经交叉上核的自然频率。在模型中， ωi是通过分布函数g(ωi)取得的，我们取的是在24小时内的最大值ω 。右边第二个加数描述的是每一个视神经交叉上核与其他神经元之间同步的概率，其耦合强度为K 。第三个加数则表示的是与外部的联系，特别是太阳光的影响。它影响的强度为F ，每个神经元都有一个相位δt + p ，其中δ= 2πhr/(24s) ，他代表的是每日的频率， p相位依赖于时区。如果t是格林威治标准时间， p为正数，在格林威治东边， p的取值范围为0 < p <π；若在西边，则为-π< p < 0 。
看上去这个等式十分简单，但是它仍然需要巨大的数据量，每一组等式所需要的数据大概在N-10^4的数量级上。因此为了能够进一步简化等式，我们在这里提出两种方法。第一步，我们取连续极限：N→∞ ，则SCN的状态取决于调节神经元的相位和频率随时间分布的函数， f(θ,ω,t) 。当N>>1时， N→∞的极限才能有很好的近似。第二，我们使用通常所说的奥特——安东森假设（Ott-Antonsen ansatz），这个假设为解出分布函数f提供了非常好的方法。当简化系统转化为连续介质系统时，该假设为f(θ,ω,t)限定了函数表达式。更进一步地，注记[6]发现在一个条件较为宽松而且长时间的状态下， f会在一定概率下收敛到简化条件的解上。因此，我们捕捉每一个汇点和分叉点。在自然调节频率:

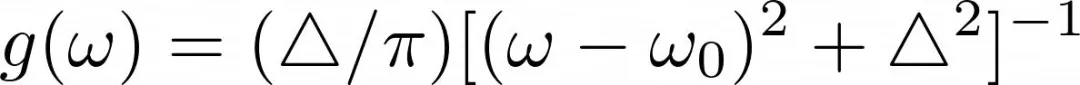
文章图片

的洛伦兹分布情况下， SCN的宏观状态将由一个单一复数变量

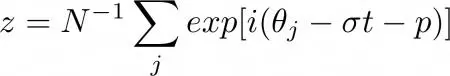
文章图片

来表示，我们由此得到如下公式：

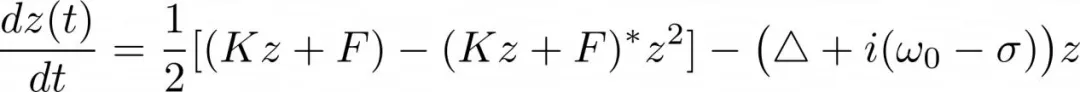
文章图片

其中复变量z的极角表示的是SCN的总体全局视神经上核相位。因此我们的假设将一个N维系统简化为这种单一，一致性的复数常微分方程，以使我们能够快速遍历每一个变量空间，并能对动态系统有更深刻的理解。
尽管假说仍然需要对等式1所表示的宏观状态行为进行研究，这种假说仍然旧展示了这种降低维度能力的作用，不仅仅对等式1有效，还对非常多的情况有作用。这些场景包括，在伦敦千禧桥上的人行横道上人致振动、约瑟夫森结电路、鸟鸣的模型建立和脉冲耦合神经元网络构建。这个模型还可加入更多额外的动态特征，例如某一个视神经上核对另一个的延时影响，不同网络拓扑、空间耦合和反馈控制模型的效果。
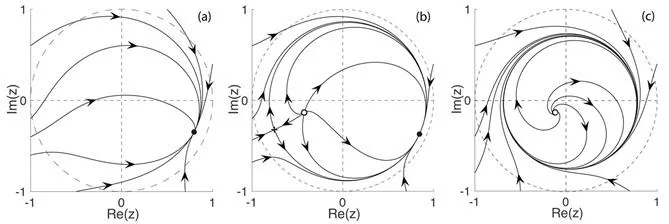
正如图像一所示，该模型是一个性质相异的动态空间，它拥有三个变量体系。我们认为一个正常人的昼夜节律是与外部24小时周期相协调的，在z相位空间中是有一个对应的固定点（在图1a和1b中的一个黑点）。图1c所示的状态是一个人的昼夜周期节律与外部24小时周期是不同步的。该图表明这个人的昼夜相位和外部刺激的相位变化曲线最终形成了一个封闭曲线，在z相位上组成一个周期性轨道。图1a和图1b的动态关系之间其实也有差别；通过鞍结分岔过程处理，除了对应的固定点，图1b还有两个另外的固定点，一个不稳定（显示成未闭合的圆）和一个鞍结（表示成一个交点）。鞍结的不稳定特性就形成了一个环，而且z相位可以通过两个相反的方向到达固定点。

文章图片

为了能够分析健康人从时差反应中恢复过来的过程，我们假设旅行者是从他之前的时区（z相位是在固定的位置）来到目前的位置的。为了简化分析过程，我们同时假设旅行者的跨时区旅程非常快，因此建立这个方程的时候在公式一中p的变化会是不连续的。因此，在旅行的最后，状态变量z会迅速被[p(initial)-p(final)]旋转后的(|z|fixed)所代替。 z相位地固定点回到他之前的固定点前边还是后边取决于旅行结束的位置。我们比较感兴趣的是恢复过程中存在的东向和西向的不对称性，和以及恢复到正常状态的时间。我们用一系列通用的变量代表了一个健康人的各项指标。图1a表示的便是变量集作用后生成的图像，这张图中只有一个固定点是稳定的。当外部刺激不存在时，视神经交叉上核神经元集合平均调整时间为24.5小时，和外部实验观察类似。这个计算结果也意外地表明自然状态下，正常人视神经交叉上核神经元调节周期为24小时，与实验结果有一个比较小的差距（约30分钟），这也就足以说明东西向时差反应的不对称性是比较明显的。
【调节|时差反应东西向不对称性的解释】在动态系统应用的SIAM会议上（DS17），爱德华·奥特将会出席朱桢·摩斯尔名为“大型多个联动的昼夜调节器的应急行为”的讲座。该讲座将于今年五月在犹他州雪鸟市举行。他同时会组织并在“使用备用电脑来学习动态系统”的系列讲座上发表讲话，而米歇尔·吉瓦将会在“对称性、非对称性和网络同步”的系列讲座上发表演讲。
关注哆嗒数学网每天获得更多数学趣文

调节|时差反应东西向不对称性的解释

推荐阅读

小米路由器未能获取上网模式怎么解决

怎样做小学生读书小报

我们在日常生活中怎样有效的保护自己

表达人生哲理的诗句

植物需要的营养成分

顺德惠企平台企业用户申请贴息流程

英法德三国哪国人口最多

爆破专业需要学习那些知识

小区物业管理系统是什么？

焦作到恩施多少公里请看距离

跟女朋友分手后祝福话

不烂子的做法（土豆）

有哪些运动员是向娱乐圈发展的？

后肩胛骨痛的原因

幼儿园课堂表扬方式有哪些

下午和晚上能练八段锦吗

快速阅读的方法训练怎样能快速阅读

手机没反应怎么解决

生什么义组成语

思明州市属于哪一个省三明属于哪个省份哪个市