电磁学中极为重要的连续性方程,一个简单的证明
文章图片

文章图片

文章图片
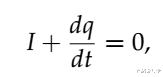
连续性方程在物理学中是至关重要的 , 因为它告诉我们什么物理量在什么条件下必须守恒 。 就电磁学而言 , 必须守恒的最基本的量是电荷q , 即流经空间某一区域(如电流)的总电荷量 。 连续性方程为:
- 方程1:微分形式的电荷的连续性方程
是电流密度J的散度(是流过某个横截面积的电流量)和
是电荷密度\uD835\uDFBA在空间各点相对于时间的变化率 。 这是通量守恒的直接结果 。 我们也可以在积分的背景下看这个表达式:在方程的两边对体积进行积分 , 可以得到:
利用导数和积分是线性运算符的事实 , 我们可以从第二项的积分中取出时间导数 。 此外 , 通过对第一项应用散度定理 , 我们可以将方程改写为:
- 方程2:积分形式的电荷的连续性方程
- 方程3:电荷守恒
推荐阅读
- 真的存在“布罗肯幽灵”吗?那个隐藏在云雾中的巨人,到底是谁?
- 从大自然中汲取灵感,突破性的“细胞流体”技术可能会产生广泛的影响
- 律师分析:“二手房”买卖交易过程中,有哪些常见法律风险?
- 民工捡到金手镯,确认是文物并主动上交,却被考古队长中饱私囊
- 15000年前海底金字塔被发现,科学家推测:中华文明前身是MU文明
- 中科西部干细胞研究院:干细胞如修理大师,调整失控的免疫系统!
- 中国空间站太阳能转化效率30%!美国不服:我换电池
- 1到10之间最神秘的数字,中外无数传说都和它有关,谜团至今未解
- 在国际空间站中,人类可能受到的伤害
- ?微波和射频技术在量子计算中还有许多其他关键应用







