易坊好文馆

  1. 首页 > 生活百科 >

42，一点都不乏味

42，一点都不乏味
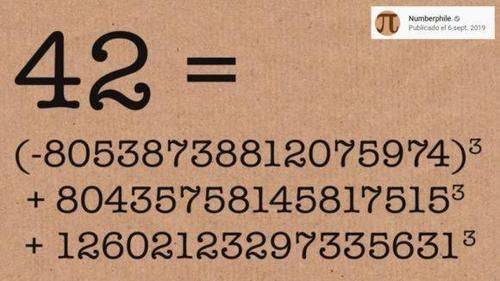
文章插图
42，一点都不乏味
好吧，这早已不是秘密了。
>>>>
我在前言里曾说过，这个数在道格拉斯·亚当斯的《银河系搭车客指南》里很重要，它是“关于生命、宇宙以及一切之终极问题”的答案。这 一发现马上产生了一个新问题：什么才是真正的关于生命、宇宙和所有一切之终极问题？亚当斯说，他选择这个数是因为，他快速地问了一圈朋友们，大家都认为是最乏味的。
在此，我想保护不受这样的诽谤。就数学意义而言，毫无疑问无法和、 ，甚至是相提并论。然而，它也并不是完全无趣的。是普洛尼克数、卡塔兰数，也是最小的魔方幻方常数。当然，它还有一些其他特点。
▌普洛尼克数
所谓普洛尼克数（也叫长方形数、矩形数或 heteromecic 数）是指两个连续整数的积，因此它的形式是。当时，我们可以得到。由于第个三角形数是
，所以普洛尼克数是三角形数的倍。它还是前个偶数之和。数量是普洛尼克数的点可以排列成一个矩形，这种矩形的一条边比另一条边大（图 171）。
42，一点都不乏味
文章插图
图 171 前 6 个普洛尼克数。阴影部分表示它们为什么是三角形数的 2 倍
这里有一个关于高斯的故事，在他还很年轻的时候，被老师要求完成一个一般形式的问题
很快发现，如果相同的和式以递减的顺序写出来，即
其相应的数对之和都等于 。因为有对这样的数对，所以它们的总和为，这是一个普洛尼克数。老师提出的问题的答案是这个数的一半，即。然而，我们实际上并不知道高斯的老师在课上提出的问题到底是什么，它有可能更难。如果是这样的话，那么高斯就更聪明了。
▌第个卡塔兰数
卡塔兰数出现在许多不同的组合问题里，所谓组合问题是指对各种数学任务的完成方法进行计数。这个问题可以追溯到欧拉，他计数了一个多边形可以分割成多少种顶点相接的三角形。后来，欧仁·卡塔兰发现了这类问题和代数之间的联系：在加法或乘法算式里插入括号的方法有多少种。我很快就会做解释，但首先让我先介绍一下这类数。
对 n = 0, 1, 2,…而言，前几个卡塔兰数 Cn
利用阶乘可以得到如下公式：
当比较大时，它还有一个很好的近似公式：
这又是一个在看似和圆或球体无关的问题里出现了的例子。
是把正边形分割成三角形的不同方法的数量（图 172）。
42，一点都不乏味
文章插图
图 172 把六边形分割成三角形的 14 种方法
它也是生成有片叶子的二叉树的数量。二叉树源于一个根节点， 然后从这个节点开始向两边分枝。每个分枝都以点或叶子结束。每个点必须继续分出两枝（图 173）。
图 173 5 棵有 4 片叶子二叉树
如果你觉得这个想法有点难懂，那么它和代数还有一个更直接的联系——计算在加法或乘法算式中插入括号的方法的总数，例如对 abcd 而言， 有C5 种可能：
一般而言，个符号有种插入括号的方法。为了搞明白其中的联系， 我们可以把这些符号顺次填在树的叶子上。如果一对叶子有相同的节点，
那么就插入括号。如图 174 所示，我们先从左往右把片叶子标上、 、 、 。然后，从下往上在连接和的节点旁标记。它上面的节点连接了和标记为的节点，因此新的节点对应于。最后，顶上的节点连接了和，因此，它是。
42，一点都不乏味
文章插图
图 174 把二叉有根树转化成代数
许多其他的组合问题也会出现卡塔兰数；以上是最容易描述的一小部分。
▌魔方
一个魔方的幻方常数是。这样的魔方包含了每个数各一次，平行于棱边的每行或经过中心的对角线中的数之和是相等的——这个和被称为幻方常数。所有个数之和是。这些数可以被分成组不相交的三元组，而每个三元组相加后可以得到幻方常数，因此幻方常数必须是
。
这样的排列是存在的，图 175 就是一个例子。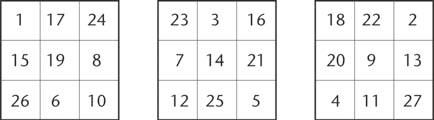
42，一点都不乏味
文章插图
图 175魔方的连续三层
▌其他特点
■是分拆的不同方法的数量，拆分需按自然顺序把数写成整数之和，如
■是第二个楔形数，所谓楔形数是指个不同质数之积。在这里， 。前几个楔形数分别是
■是第三个边形数，它和三角形数类似，但基于的是正边形。
■是超级多重完全数：除数之和的除数之和（包括），这样重复次之后的数字等于自己。

推荐阅读


上一篇：化工业 注意！基金和外资悄悄加仓这个方向！

下一篇：如果亚马逊雨林被彻底烧毁，可能会发生在地球上的11件事